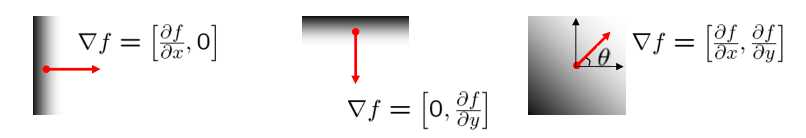Canny边缘检测算法原理及代码实现

1. 算法原理

Canny算法是由J. Canny 于1986年在Pattern Analysis and Machine Intelligence(简称：PAMI)杂志上发表的 A Computational Approach To Edge Detection 文章中提出，其很好的解决了在其他边缘检测算法中的存在的宽边与伪边的问题，至今仍是边缘检测算法中广为使用的算法。

Canny算法的实现一共可分为四个步骤：

对图像进行高斯模糊处理
求出图像的梯度图像及梯度方向矩阵
对梯度图像进行非极大化抑制，使宽边变为细边
对生成的非极大化抑制结果图进行滞后阈值法，用强边延伸弱边，解决伪边问题

1.1 高斯滤波处理

高斯滤波处理的目的是降低图像中噪声对检测结果的干扰，一般设置高斯核大小为 3×3 。

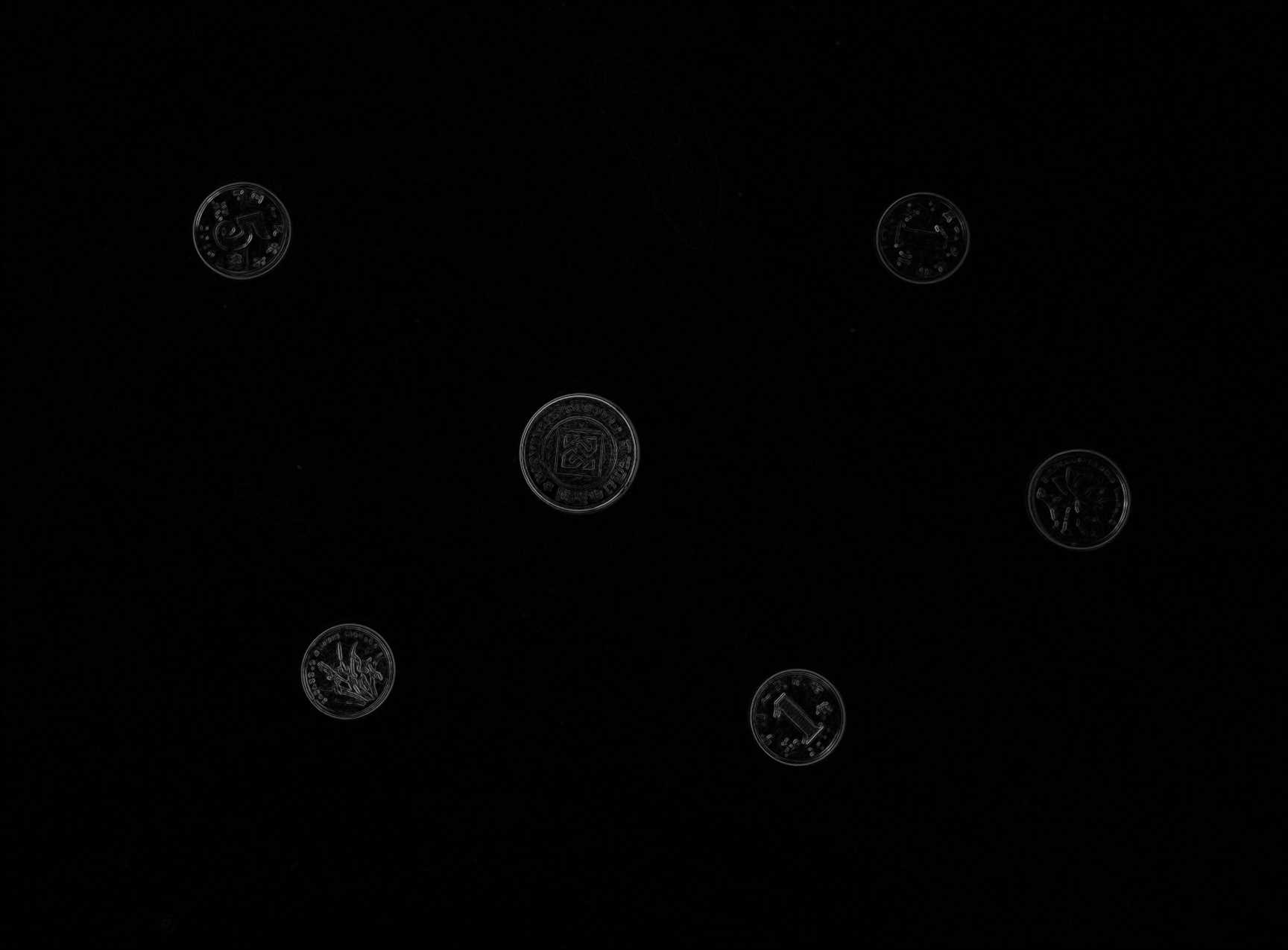
1.2 计算梯度图像及梯度方向矩阵

梯度图像即图像的一个粗略的边缘图像，其中包含一些宽边和伪边。

图像边缘的特征是此处的像素值发生突变，为了反应突变的程度大小，可以使用导数来计算。导数公式如下：
$\frac{\partial f(x,y)}{\partial x} =\lim_{\varepsilon \to 0} \frac{f(x+\varepsilon ,y)-f(x,y)}{\varepsilon }$
但由于图像的坐标x和y是离散的，所以可以将以上公式近似为：
$\frac{\partial f(x,y)}{\partial x} = \frac{f(x+1 ,y)-f(x,y)}{1 }$
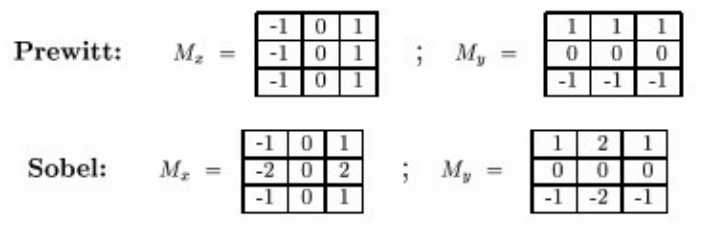
这样就形成了一个简单的检测算子[-1,1]，拿此算子遍历整个图像就可以得到x方向的边缘。（y方向与此类同）

还有其他优秀的边缘检测算子，如Prewitt，Sobel等等。

得到x与y方向的导数图像后，计算每个像素的梯度，梯度的公式如下：
$\bigtriangledown f=[\frac{\partial f}{x}, \frac{\partial f}{y}]$

其表示为与该像素处边缘垂直的一个向量，此向量的方向为梯度方向，此向量的大小（即向量的模长）为边缘的强度。
$\theta =tan^{-1} (\frac{\partial f}{y}/\frac{\partial f}{x}) \qquad\qquad||\bigtriangledown f||=\sqrt{(\frac{\partial f}{x})^{2}+(\frac{\partial f}{y})^{2} }$
由梯度模长组成的矩阵所对应的图像为梯度图像，由\theta组成的矩阵即为梯度方向矩阵。此时的方向也可由正切值来表示。

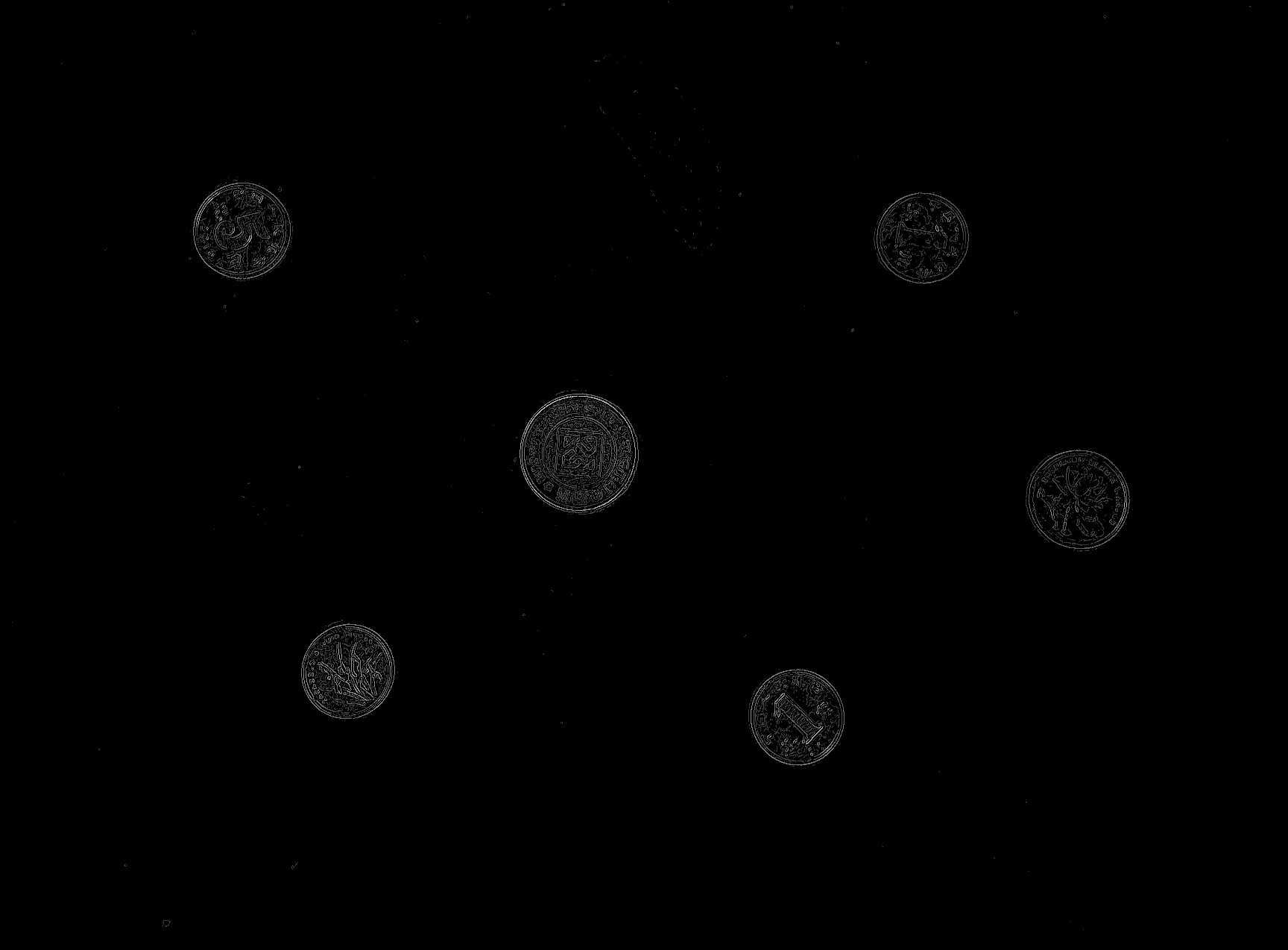
1.3 非极大化抑制

非极大值抑制的目的在于细化边缘，将原有粗略边缘检测图中的宽边细化为真正的边缘，从而可以更好的凸显物体的轮廓。
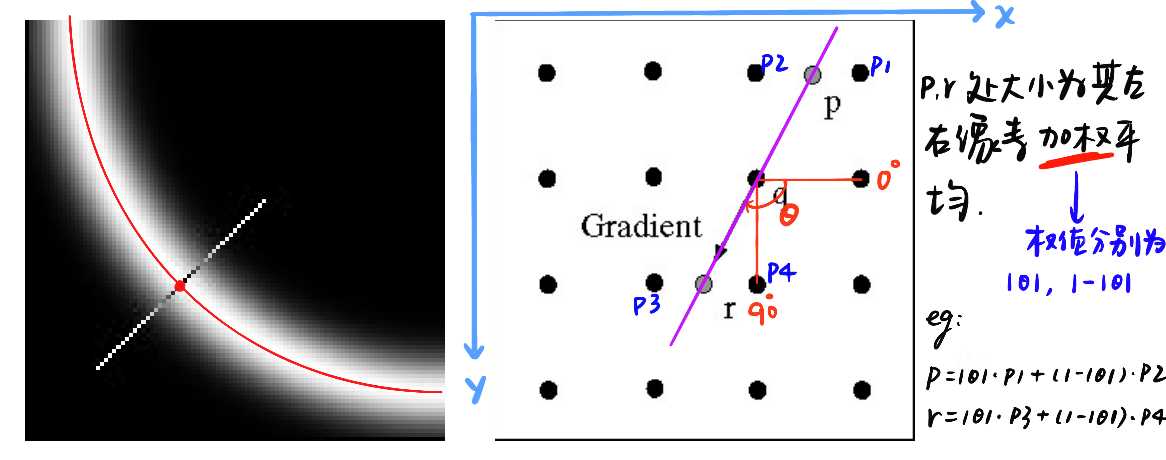
非极大化抑制的原理是在每个像素的梯度方向，检查此像素是不是极大像素点，如果是，则保留此像素点，如果不是，将其像素置为0。若该像素的梯度方向并非在特定角度（0度、45度等），则采用软像素（即为两边像素的加权和），大致思路如下图：

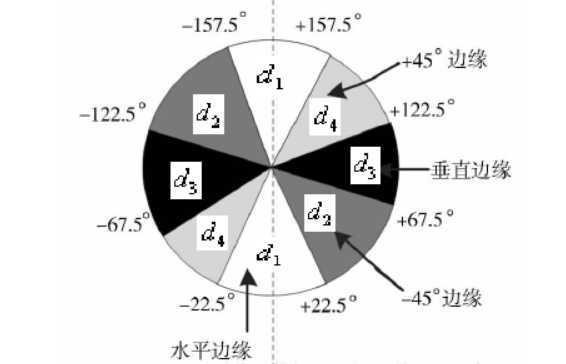
当然也可以使用角度量化，直接将该像素与周围其他像素对比。具体如何量化见下图：

两种方法不分优劣，在不同的场景下显现的效果大致相同。

1.4 滞后阈值处理

滞后阈值处理目的在于去除伪边。

滞后阈值处理即双阈值处理，原理是先用高阈值删选出一定是边缘的像素，再用低阈值进行边的延伸。此处因为已经做了非极大化抑制，所以不同考虑方向的问题，直接可以遍历周围8个像素点，如果有大于高阈值的像素点存在，那么该像素点就视为延伸出来的边，将其像素拉高，并将此改变返回给图像，以此类推。没有延伸到的像素将其像素值置为0即可。最后得到的边缘即为真正的图像边缘，也就是Canny算法得到的最终结果。

2. 算法实现

import cv2
import numpy as np

class Canny:

    def __init__(self, Guassian_kernal_size, img, HT_high_threshold, HT_low_threshold):
        ''' 初始化canny类 :param Guassian_kernal_size: 高斯滤波器尺寸 :param img: 输入的图片，在算法过程中改变 :param HT_high_threshold: 滞后阈值法中的高阈值 :param HT_low_threshold: 滞后阈值法中的低阈值 '''
        self.Guassian_kernal_size = Guassian_kernal_size
        self.img = img
        self.HT_high_threshold = HT_high_threshold
        self.HT_low_threshold = HT_low_threshold
        self.y, self.x = img.shape[0:2]
        self.sobelX = np.array([[-1,0,1]])    # x方向检测算子
        self.sobelY = np.array([[-1],[0],[1]])    # y方向检测算子
        self.angle = np.zeros([self.y, self.x])
        pass

    def Get_gradient_img(self):
        ''' 计算梯度图和梯度方向矩阵。 :return: 生成的梯度图 '''
        print("Get_gradient_img")

        DerivativeImg_X = np.zeros([self.y, self.x], dtype=np.float)
        DerivativeImg_Y = np.zeros([self.y, self.x], dtype=np.float)
        for i in range(0, self.y):
            for j in range(0, self.x):
                if i == 0 or j == 0 or i == (self.y - 1) or j == (self.x - 1):
                    DerivativeImg_X[i][j] = 0
                else:
                    DerivativeImg_X[i][j] = np.sum(self.sobelX * self.img[i:i + 1, j - 1:j + 2])
                    DerivativeImg_Y[i][j] = np.sum(self.sobelY * self.img[i - 1:i + 2, j:j + 1])
        
        gradient_img, self.angle = cv2.cartToPolar(DerivativeImg_X, DerivativeImg_Y)
        self.angle = np.tan(self.angle)
        self.img = gradient_img.astype(np.uint8)

        return self.img

    def Non_maximum_suppression (self):
        ''' 对生成的梯度图进行非极大化抑制，将tan值的大小与正负结合，确定离散中梯度的方向。 :return: 生成的非极大化抑制结果图 '''
        print("Non_maximum_suppression")

        result_img = np.zeros([self.y, self.x])
        for i in range(1, self.y - 1):
            for j in range(1, self.x - 1):
                if abs(self.img[i][j]) <= 5:
                    result_img[i][j] = 0
                    continue
                # __ g2 __
                # C
                # __ g4 __
                elif abs(self.angle[i][j] > 1):
                    gradient2 = self.img[i - 1][j]
                    gradient4 = self.img[i + 1][j]
                    # g1 g2
                    # C
                    # g4 g3
                    if self.angle[i][j] > 0:
                        gradient1 = self.img[i - 1][j - 1]
                        gradient3 = self.img[i + 1][j + 1]
                    # g2 g1
                    # C
                    # g3 g4 
                    else:
                        gradient1 = self.img[i - 1][j + 1]
                        gradient3 = self.img[i + 1][j - 1]
                # __ __
                # g2 C g4
                # __ __
                else:
                    gradient2 = self.img[i][j - 1]
                    gradient4 = self.img[i][j + 1]
                    # g1
                    # g2 C g4
                    # g3
                    if self.angle[i][j] > 0:
                        gradient1 = self.img[i - 1][j - 1]
                        gradient3 = self.img[i + 1][j + 1]
                    # g3
                    # g2 C g4
                    # g1
                    else:
                        gradient1 = self.img[i + 1][j - 1]
                        gradient3 = self.img[i - 1][j + 1]

                temp1 = abs(self.angle[i][j]) * gradient1 + (1 - abs(self.angle[i][j])) * gradient2
                temp2 = abs(self.angle[i][j]) * gradient3 + (1 - abs(self.angle[i][j])) * gradient4
                if self.img[i][j] >= temp1 and self.img[i][j] >= temp2:
                    # 此处的 +50 是将像素值拉高50，为了观察结果方便，后面的双阈值也应该相应的拉高50
                    result_img[i][j] = self.img[i][j] + 50	
                else:
                    result_img[i][j] = 0
        self.img = result_img.astype(np.uint8)
        
        return self.img

    def Hysteresis_thresholding(self):
        ''' 对生成的非极大化抑制结果图进行滞后阈值法，用强边延伸弱边，这里的延伸方向为梯度的垂直方向， 将比低阈值大比高阈值小的点置为高阈值大小，方向在离散点上的确定与非极大化抑制相似。 :return: 滞后阈值法结果图 '''
        print("Hysteresis_thresholding")

        result_Img = self.img.copy()
        for i in range(1, self.y - 1):
            for j in range(1, self.x - 1):
                if self.img[i][j] < self.HT_low_threshold:
                    result_Img[i][j] = 0
                elif self.img[i][j] < self.HT_high_threshold:
                    if (self.img[i - 1][j - 1] >= self.HT_high_threshold or 
                        self.img[i - 1][j] >= self.HT_high_threshold or 
                        self.img[i - 1][j + 1] >= self.HT_high_threshold or 
                        self.img[i][j - 1] >= self.HT_high_threshold or 
                        self.img[i][j + 1] >= self.HT_high_threshold or 
                        self.img[i + 1][j - 1] >= self.HT_high_threshold or 
                        self.img[i + 1][j] >= self.HT_high_threshold or 
                        self.img[i + 1][j + 1] >= self.HT_high_threshold):
                        result_Img[i][j] = 255 
                    else:
                        result_Img[i][j] = 0
                else:
                    result_Img[i][j] = 255
                self.img = result_Img            

        return self.img

    def canny_algorithm(self):
        ''' 按照顺序和步骤调用以上所有成员函数。 :return: Canny 算法的结果 '''
        self.img = cv2.GaussianBlur(self.img, (self.Guassian_kernal_size, self.Guassian_kernal_size), 0)
        self.Get_gradient_img()
        self.Non_maximum_suppression()
        self.Hysteresis_thresholding()
        pass