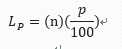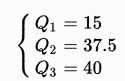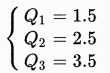四分位数 箱线图

四分位数 箱线图

开头语：本人建议采用Origin来制作箱线图

1、作用

箱线图（Boxplot）也称箱须图（Box-whisker Plot），它是用一组数据中的最小值、第一四分位数、中位数、第三四分位数和最大值来反映数据分布的中心位置和散布范围，可以粗略地看出数据是否具有对称性。通过将多组数据的箱线图画在同一坐标上，可以用于多组数据平均水平和变异程度的直观分析比较。

2、什么是四分位数^[1]

（1）概念：

四分位数（Quartile）是统计学中分位数的一种，即把所有数值由小到大排列并分成四等份，处于三个分割点位置的数值就是四分位数。

• 第一四分位数 (Q₁)，又称“较小四分位数“，等于该样本中所有数值由小到大排列后第25%的数字。
• 第二四分位数 (Q₂)，又称“中位数“，等于该样本中所有数值由小到大排列后第50%的数字。
• 第三四分位数 (Q₃)，又称“较大四分位数“，等于该样本中所有数值由小到大排列后第75%的数字。

第三四分位数与第一四分位数的差距又称四分位距（InterQuartile Range, IQR）。

（2）运算过程：

关于四分位数值的选择尚存争议，origin软件采用该算法。

主要选择四分位的百分比值（p），及样本总量（n）有以下数学公式可以表示：

• 情况1:如果 L 是一个整数，则取第 L 和第 L+1 这两个位置数值的平均值
• 情况2:如果 L 不是一个整数，则取下一个最近的整数。（比如 L=1.2，则取位置为第2个的数值）

（3）举例：

一个算法如下：

1. 利用中位数使数据分成两列（不要把中位数放入已分好的数列），
2. 第一四分位数为第一组数列的中位数；第三四分位数为第二组数列的中位数。

以下例子可以用来参考。

例 1
数据总量:

6, 47, 49, 15, 42, 41, 7, 39, 43, 40, 36

由小到大排列的结果:

6, 7, 15, 36, 39, 40, 41, 42, 43, 47, 49

例 2
数据总量: 7, 15, 36, 39, 40, 41

例 3
数据总量: 1, 2, 3, 4

3、箱线图的结构^[2]：

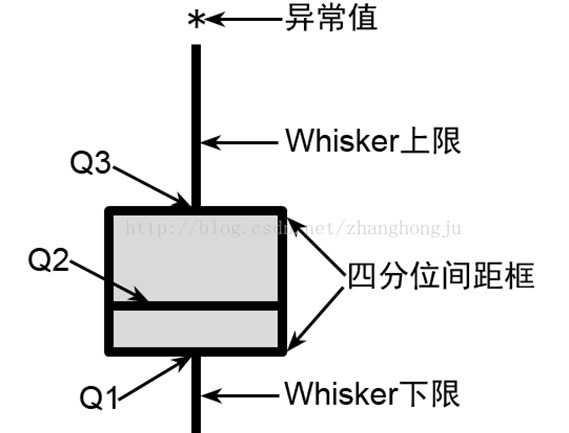
箱线图包括一个矩形箱体和上下两条竖线，箱体表示数据的集中范围，上下两条竖线分别表示数据向上和向下的延伸范围，结构如图 1所示。

图 1箱线图的结构

四分位间距框的顶部线条是第三四分位数的位置，即Q3，表示有75%的数据小于等于此值。底部线条是第一四分位数的位置，即Q1，表示有25%的数据小于此值。则整个四分位间距框所代表的是数据集中50%（即75%-25%）的数据，四分位间距框的高度就是这些数据涉及的范围，能够表现出数据的集中程度。Q2是数据中位数的位置。

Whisker上限是延伸至距框顶部1.5倍框高范围内的最大数据点，Whisker下限是延伸至距框底部1.5倍框高范围内的最小数据点，超出Whisker上限或下限的数值将使用星号”*“表示。

4、箱线图的绘制

由于四分位数的选择没有公论，算法有几种，各自取法不同。因此，取用的方式不一样，结果也不一样。

在Excel中，其利用QUARTILE函数计算四分位数，但是它并非采用本文所介绍的算法，其计算逻辑见附带说明“Excel QUARTILE函数计算逻辑“。另外，在Excel中绘制箱线图需要借助股价图来实现，因此无法展现异常值，Whisker上限将延伸至数据最大值的位置，Whisker下限将延伸至数据最小值的位置^[2]。

因此，作者建议采用Origin来制作箱线图，该软件的四分位数计算方式正是采用上述的算法，同时它也解决了Excel提到的问题。

origin的简单操作步骤如下：

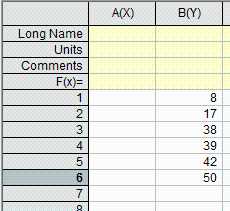
（1）打开Origin，示例数据如下：

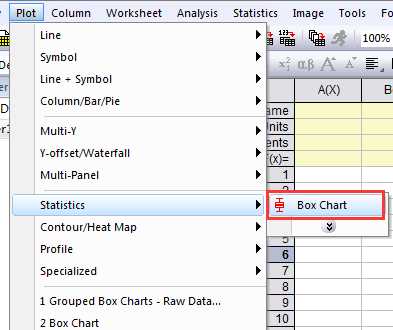
（2）选中该列数据，选择Plot—Statistics—Box Chart

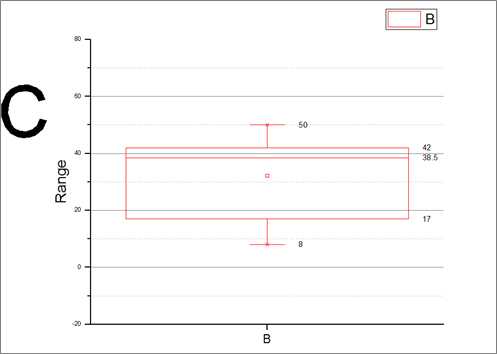
输出结果：

*附带说明：“Excel QUARTILE函数计算逻辑“^[3]

微软网站关于 Excel 上 QUARTILE()函数的计算逻辑如下：

1) Find the kth smallest member in the array of values, where: 

k=(quart/4)*(n-1))+1

If k is not an integer, truncate it but store the fractional portion (f) for use in step 3. And where：（如果k不是整数，截取它并保留小数部分f用于第三步的计算）

• quart = value between 0 and 4 depending on which quartile you want to find（0到4之间的四分位点）
• n = number of values in the array（一组数值的个数）

2) Find the smallest data point in the array of values that is greater than the kth smallest – the (k+1)th smallest member.

3) Interpolate between the kth smallest and the (k+1)th smallest values:

Output = a[k]+( f * (a[k+1]-a[k]) )

其中，a[k] = the kth smallest, a[k+1] = the k+1th smallest

示例：

计算这组数据0,2,3,5,6,8,9的第3四分位数，步骤如下：

1)计算k和f

k=TRUNC((3/4*(7-1))+1)=5

f=(3/4*(7-1))-TRUNC(3/4*(7-1))=.5

2)第k（即5）个最小值是6,第k+1（即6）个最小值是8.

3)计算第3四分位数:

Q₃=6+(.5*(8-6))=7

参考资料：

[1]维基百科，https://zh.wikipedia.org/wiki/%E5%9B%9B%E5%88%86%E4%BD%8D%E6%95%B0

[2] http://blog.csdn.net/zhanghongju/article/details/18446131

[3] http://blog.csdn.net/kiddii/article/details/52690140

今天的文章四分位数 箱线图分享到此就结束了，感谢您的阅读。