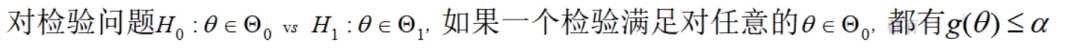1.假设检验是建立在小概率事件原理上的一种反证法
2.小概率事件原理指的是小概率事件在一次随机试验中一般是不可能发生的
3.假设检验通常有四步:建立假设;选择检验统计量,给出拒绝域形式;选择显著性水平和确定拒绝域;做出判断
4.因为样本随机性,会导致检验犯第一类错误(弃真)和第二类错误(取伪)
5.弃真错误(α)与取伪错误(β)不能同时减小,通常采取折中方案,仅限制第一类错误,这就是显著性检验
6.样本观测值落在拒绝域内的概率称为势函数,对于原假设上所有参数,势函数均不大于α,则该检验称为显著性水平为α的显著性检验
7.样本观测值能够作出拒绝原假设的最小显著性水平称为检验的p值
假设检验(hypothesis test)是统计推断上很重要的知识。小编经过深思熟虑,自己对这四个字下了如下定义:
假设检验,就是根据有限的证据引向一个有效的命题,并用统计方法检验该命题的可信度。
1.例子引入
引用《概率论与数理统计教程第二版》的例子,先来感受一下假设检验的思想。
(女士品茶试验)一种奶茶由牛奶与茶按一定比例混合而成以先倒茶后倒奶(记为TM),也可以反过来(记为MT)。某女士声称她可以鉴别是TM还是MT,周围品茶的人对此产生了议论,“这怎么可能呢?”“她在胡言乱语”“不可想象”在场的费希尔也在思索这个问题,他提议做一项试验来检验如下假设(命题)是否可以接受
假设H:该女士无此种鉴别能力
他准备了10杯调制好的奶茶,TM与MT都有服务员一杯一杯地奉上,让该女士品尝,说出是TM还是MT,结果那位女士竟然正确地分辨出10杯奶茶中的每杯这时该如何对此作出判断呢?
费希尔的想法是:假如假设H是正确的,即该女士无此种鉴别能力,她只能猜,每次猜对的概率为1/2,10次都猜对的概率为2^(-10)<0.001,这是一个很小的概率,在一次试验中几乎不会发生的事件,如今该事件竟然发生了,这只能说明原假设H不当,应予以拒绝,而认为该女士确有辨别奶茶中TM与MT的能力。
从上面例子我们来理解建设检验的思想,它依据的是小概率事件原理:小概率事件在一次随机试验中一般是不可能发生的。做出判断的思维方式是:假如试验结果与假设H发生矛盾就拒绝原假设H,否则就接受原假设
2.假设检验的步骤
根据假设检验的原理与判断方式,我们给出假设检验的五个基本步骤:
step1:建立假设(原假设与备择假设):根据实际问题,建立统计假设H0 vs H1
step2:选择检验统计量,给出拒绝域形式:选取一个合适的检验统计量T(X),使得当H0成立时T的分布完全已知,并根据H0及H1的特点,确定拒绝域W的形状
step3:选择显著性水平和确定拒绝域:确定显著性水平α,确定具体的拒绝域W
step4:做出判断:由样本观测值计算检验统计量T,由T是否属于W,做出最终判断
建立假设
在假设检验中,通常将不宜轻易加以否定的假设作为原假设
选择检验统计量,给出拒绝域形式
当有了具体的样本后,按照法则就可决定是接受H0还是拒绝H0,即检验就等价于把样本空间划分成两个互不相交的部分W和V,当样本属于W时,拒绝H0;否则接受H0。我们称W为该检验的拒绝域,而V称为接受域。
由样本对原假设进行检验总是通过一个统计量完成的,该统计量称为检验统计量
比如如果要检验的假设是正态总体均值,那么样本均值就是一个很好的统计量,在方差已知场合,样本均值是总体均值的充分统计量。
通常我们将注意力放在拒绝域上。正如在数学上我们不能用一个例子去证明一个结论一样,用一个样本不能证明一个命题是成立的,但可以用一个样本推翻一个命题。因此,从逻辑上,注重拒绝域是适当的。
显著性水平
由于样本是随机的,故当我们应用某种检验作判断时,我们可能做出正确的判断,也可能做出错误的判断。因此,我们可能犯两种错误:
1.H0为真但判别为拒绝,此类错误为“弃真”错误,即将真的当成假的,也称为第一类错误
2.H0为假并被接受,此类错误称为“取伪”错误,即将假的当成真的,也称为第二类错误
| 结论 | H0为真 | H0为假 |
| 接受H0 | 正确 | 第二类错误 |
| 拒绝H0 | 第一类错误 | 正确 |
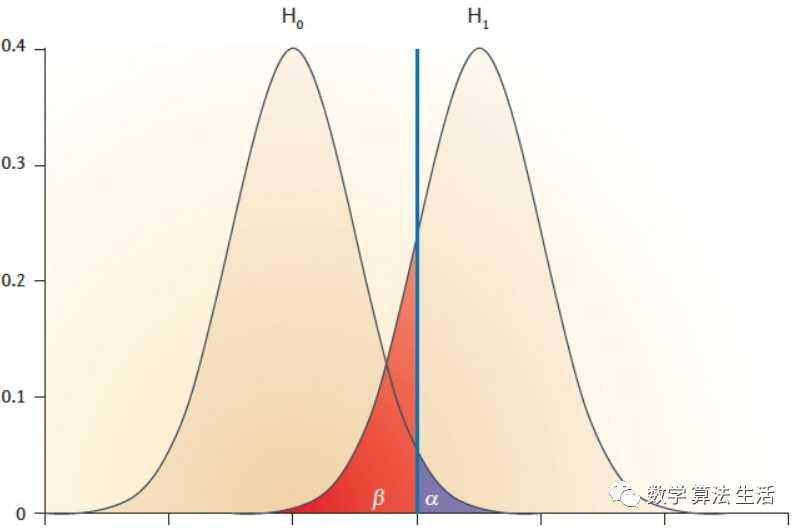
我们把犯第一类错误的概率记为α,犯第二类错误的概率为β。那有没有办法使得这两类错误的概率都尽可能小呢。实际上做不到这一点。我们通过一个例子来说明。
对于在显著性水平为α(图中蓝色直线)的假设H0,对于第一类错误,也就是H0为真的情况下样本点落到α区域,那么它犯错的概率也就是α;对于第二类错误,假设真正的分布是H1,也就是说,样本是从H1分布抽取出来的,而计算的时候是当成H0分布,故而,我们接受了一个错误的假设H0,这个犯错误的概率是由H1与H0分布交集决定的(图中红色部分)。因为无法拒绝H0,只能被迫接受,所以,第二类错误,本质上是无法被证伪。
很显然,如果减小α,β会增大。因此,一个检验无法使得犯第一类、第二类错误同时变小。在样本量给定的条件下,α与β中一个减小必导致另一个增大,这具有一般性。进一步地说,在样本量一定的条件下不可能找到一个使α、β都小的检验。
为此,我们采取折中方案,通常仅限制犯第一类错误的概率,这就是显著性检验。为此,先介绍势函数。
则称该检验是显著性水平为α的显著性检验,简称水平为α的检验
最常用的选择是α=0.05,有时也选择0.1或0.01
给出拒绝域与做出判断
在确定显著性水平后,我们就可以定出检验的拒绝域W。
比如正态分布的双侧检验:
-
如果由样本数据计算的数值落在该分布的接受域内,即落在1-α这个大概率区间内,则没有理由拒绝H0, 就要接受H0
-
如果数值落在该分布的拒绝域内,即落在α这个概率区间内,就应拒绝H0,接受备择假设H1。 因为在原假设H0为真的条件下,远离原假设参数( µ=…)的事件是小概率事件,而 小概率事件在一次随机试验中一般是不能发生的
3.显著性检验的p值
根据显著性水平,我们就可以对假设进行判断。因此也带来一个问题:在一个较大的显著性水平(比如α=0.05)下得到拒绝原假设的结论,而在一个较小的显著性水平(比如0.01)下却会得到相反的结论,这种情况在理论上很容易解释:因为显著性水平变小后会导致检验的拒绝域变小,于是原来落在拒绝域中的观测值就可能落入接受域,但这种情况在应用中会带来一些麻烦:假如这时一个人主张选择显著性水平α=0.05,而另一个人主张选α=0.01,则第一个人的结论是拒绝H,而后个人的结论是接受H,我们该如何处理这一问题呢?
由此,我们用检验p值来衡量:
在一个假设检验中,利用样本观测值能够作出拒绝原假设的最小显著性水平称为检验的p值。
如果α<p,则在显著性水平α下接受H0;否则拒绝H0。
我们后面的检验可从两方面进行,其一是建立拒绝域,考察样本观测值是否落拒绝域而加以判断;其二是根据样本观测值计算检验的p值,通过将p值与事先设定的显著性水平α比较大小而作出判断。两者是等价的。
实际中,p很小时(如p≤0.001)即可作出拒绝结论,p很大时(如p>0.5)即接受只有当p与α接近时才需比较这样至少可减少部分争论
今天的文章假设检验(一)分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/63569.html