散列表（哈希表）_哈希表的表长怎么确定

一，散列函数、散列表

散列函数是把一个集合映射到另外一个集合，使得数据更加规整、有序、紧缩。

例如，把字符串映射到整数，把平面上的整点映射到整数，把离散的整数映射到紧缩的整数集合，等等。

散列函数（哈希函数）的值域，就是散列表（哈希表）。

二，冲突、链接法

1，冲突

散列函数其实就是把所有节点分成若干个桶，通过散列函数可以在O（1）的时间内找到这个桶，从而完成查找。

但是，对于复杂数据的节点，散列函数往往会让不同的节点进入同一个桶，即使桶的总数是节点总数的2倍以上也很难保证不会进入同一个桶。

这种不同节点进入同一个桶的情况，叫做冲突。

冲突解决办法：链接法（最简单的冲突解决办法）、开放寻址法

2，链接法

把同一个桶里面的所有节点都用一个链表串起来，查找这个桶的时候，沿着链表依次查找。

链表可以是单链表，也可以是双向链表。

假设节点总数为n，桶的数量为m，那么平均每个桶内的节点个数为n/m，我们称之为装载因子α，α可能小于1也可能大于1

如果散列函数保证每个桶是均匀的，那么单次查找时间是O（1+n/m）

如果不均匀，那么最坏的情况就是，所有的节点都在一个桶内，查找时间是O（n）

三，常见散列表

无论冲突解决办法有多好，还是要选择最合适的散列函数，尽量减少冲突。

不同的数据集有不同的特点，即使是整数到整数的映射也有不同的情况，散列函数不是千篇一律的，要根据实际情况选择最合适的。

常见的散列表：除法散列表、乘法散列表、列表散列表

其中除法散函数、乘法散列函数的自变量是整数，而列表散列函数的自变量是一串整数。

1，除法散列表

散列函数为f(k) = k mod m

一般来说，m=2^u或者m=2^u-1是一种不太好的选择，m应该远离2的幂

m取一个远离2的幂的素数，是一个比较好的选择。

2，乘法散列表

取一个常数A，0<A<1，散列函数 $f(k) = \lfloor m(kA-\lfloor kA\rfloor)\rfloor$

乘法散列表的一个有优点是对m的选择不是特别关键。

为了方便计算，可以取m=2^t，t是一个整数。

假设计算机的字长为w位，k可以用w位表示，为了方便计算，可以取A=s / 2^w, 其中0<s<2^w

kA = ks / 2^w，假设ks = r*2^w +q，即r是高位字，q是低位字

则 $f(k) = \lfloor mq/2^w\rfloor = \lfloor q/2^{w-t}\rfloor$

即f(k)就是q的二进制中前t位。

虽然这个散列方法对任何A值都有效，不过Knuth认为A接近黄金比例0.618是比较理想的。

按照这个思路，在选取s的时候，可以取最接近0.618 * 2^w的整数。

3，列表散列表

设x={x1,x2,x3…xn}

则散列函数f(x)=((((x1+c)*x2+c)……+c)*xn+c) mod m，其中c是常数，而mod m就是复合了除法散列函数。

四，散列函数之上的手法

在基础散列函数之上，还有一些常见手法。

1，全域散列法

任何一个特定的散列函数都有可能出现最坏的情况，所有节点都散列到了同一个桶中。

全域函数组：一组有限的散列函数，他们中的每一个都把关键字全域U映射到集合{0,1,2,3……m-1}，如果对于任意2个关键字 k和l 都有，从函数组中随机选取一个函数h，h(k)=h(l) 的概率不超过1/m，那么我们称这样的函数组为全域函数组。

全域散列法：在全域函数组中随机选取一个函数作为散列函数。

PS：初始化的时候选择一次即可，选定之后不再更改。

全域散列法对于任意数据的平均性能都是最好的，但是仍然可能出现最坏情况。

2，复合散列

一般来说，把2个很复杂的散列函数复合起来并没有意义。

有意义的复合散列有3种常见情况：

（1）除法的复合

几乎在所有散列函数中，最后一步都需要复合除法散列来限制应变量的大小。

中间计算过程为了防止溢出，也经常复合除法散列。

（2）数据结构转换

比如字符串，先把每个字符散列到整数，再把这个列表进行散列。

（3）数据挑选

有一个抽象散列函数就是从一个结构体中取出若干数据成员组成新的数据，这个新的数据再作为常规散列函数的输入。

3，二次散列

在普通散列函数的基础上，每个桶都不是链表，而是一个散列表，那么就称之为二次散列。

4，完全散列

如果一个散列表在最坏情况下的查找时间为O（1），那么我们就称之为完全散列。

如果二次散列的第二级散列函数选择的好，能保证没有冲突，那么这样的二次散列表就满足完全散列的要求。

《算法导论》中，有介绍如何根据全域散列函数组选择合适的函数达到这个要求。

五，开放寻址法

开放寻址法的散列函数是二元函数，把U × {0,1,2,3……m-1}映射到集合{0,1,2,3……m-1}

换句话说，普通散列函数是把每个关键字映射到一个数，二元散列函数是把关键字映射到m个值的排列A。

1，插入

对于给定的关键字，按照映射的排列A，在散列表中逐一查找，找到第一个不冲突的位置，即可插入。

2，查找

对于给定的关键字，按照映射的排列A，在散列表中逐一查找，如果查找成功或者遇到任何空位，查找结束。

3，删除

删除稍微复杂一点，因为要保证查找操作的纯粹性。

如果直接把对应节点置空，那么后面查找另外一个元素时，可能会路过这个空位，从而查找失败。

解决办法：删除的节点打上DEL标记，查找仍然只看是否是空位，而插入的话，空位和有DEL标记的都可以插入

4，缺陷

如果有删除操作，那么查找时间就不依赖于装载因子α

所以，如果有删除操作，一般就使用链接法了。

5，常用寻址散列函数

有三种常用的寻址散列函数，不过都不是均匀散列。

（1）线性探查

首先有一个辅助散列函数g把U映射到集合{0,1,2,3……m-1}，线性探查的散列函数h(k,i)=(g(k)+i)%m

也就是说，在普通散列函数的基础之上，如果有冲突，就不断往后挪，直到找到空位就插入。

这种探寻方式，很容易出现一次群集，即当元素越来越多时，探查时间为O（m）

（2）二次探查

二次探查的散列函数h(k,i)=(g(k)+f(i))%m，其中f(i) = c*i+d*i^2

二次探查的效果比线性探查好得多，但是要充分发挥效果，需要选择好c和d的值。

如果g(k1)=g(k2)，那么h(k1,i)=h(k2,i)，即这2个关键字的探查序列完全相同，这种情况导致的群集，称为二次群集。

（3）双重散列

双重散列的散列函数h(k,i)=(g(k)+i*f(k))%m，

为了保证能探查整个序列，需要保证f(k)和m互素，所以一般取m为2的幂或者为素数。

6，均匀散列

如果每个关键字的探查序列A都等可能地是m!个全排列中的一个，那么这种散列函数我们成为均匀散列。

上面的三种常用的寻址散列函数，都不是均匀散列。

线性探查和二次探查能产生m种探查序列，双重散列能产生m^2种探查序列，所以双重散列是最接近均匀散列的。

7，均匀散列性能分析

均匀散列性能分析还是以装载因子α为基础，α = n/m，n是已装载数目，m是可装载总数，α<=1

下面分析α<1时的性能。

（1）不成功查找

对于一次不成功查找，探寻次数t大于i的概率为P（t>i）=C(n,i)/C(m,i), 其中i>=0

所以P（t>i）<= α^i

探寻次数的期望为E = ∑P（t>i）<= ∑α^i = 1/(1-α)

当n=m-1时，1/(1-α)=m

（2）插入元素

插入一个元素，平均需要探查的次数不超过1/(1-α)

（3）成功查找

对于一次成功查找，假设查找的这个元素在最初插入时，表中已经装载了i个元素，即α=i/m，0<=i<n

则这个元素的探查的期望次数不超过1/(1-α) = m/(m-i)

PS：这里我个人觉得还要再加1, 不过不重要，最多也就是最终结果需要加1罢了。

对于所有元素，即i从0到n-1取值，m/(m-i)的均值为∑m/(m-i)/n = m/n * ∑1/(m-i)<=m/n * ln(m/(m-n))=-ln(1-α)/α

也就是说，一次查找的探寻时间不超过-ln(1-α)/α，

当α=0.9时，其值小于2.6

六，一致性哈希

1，一致性

在哈希表中已经有元素的情况下，如果再新增一个桶或者去掉一个桶，除了分配到这个桶元素之外，其他所有桶内元素都不需要重新分配，这就是一致性

2，一致性哈希

一致性哈希主要用于分布式系统中，利用哈希表做负载均衡，当负载增大需要增加服务器数量，或者当服务器挂掉的时候，就会涉及到数据的重新分配。

3，一致性哈希的实现思路

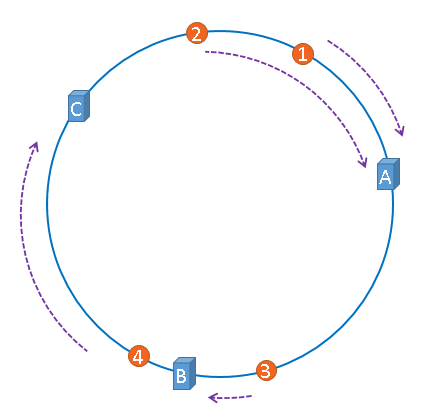
我从网友zsy的博客中，找到了这个图：

先把元素映射到0 ~ 2^32-1（即unsigned int）中的整数x，把所有的服务器也映射到这里面，并使其首尾相连成一个环，

再把x映射到某个服务器，方法是顺时针查找，找到的第一个桶（服务器）就是要放入的桶。

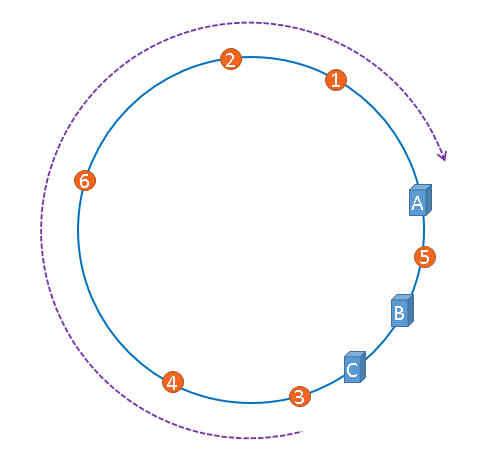
4，一致性哈希的群集

一致性哈希有2种群集：一种是数据的群集，这个就和非一致性哈希一样，另一种是桶本身的群集，如下图所示

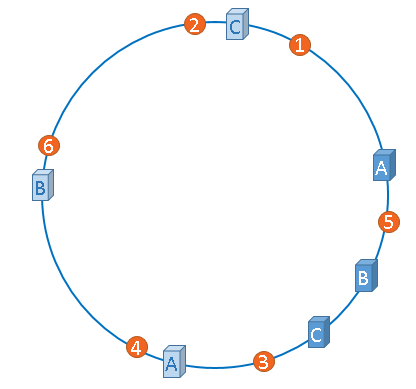
优化思路：

把整个圆环分成更多的段：

5，非一致性哈希 VS 一致性哈希

一致性哈希的优点在于，灵活伸缩，不涉及大量数据的迁移，而缺点在于，常规查找操作的时间复杂度比非一致性哈希高。

非一致性哈希平均情况下的时间复杂度是O（1），一致性哈希平均情况下的时间复杂度是O（k），其中k是桶的总数，如上图中虽然只有3个服务器，但是k=6

七，散列表的应用

1，查找

散列表用于从一个很大的表中，查找有没有一个节点和给定节点能够匹配，这种查找操作往往有很高频率。

而匹配方式，可以分为两大类：

（1）全比特匹配

这种匹配方式是，比较2个节点存储在计算机中的比特位是否完全相同。

例如，查找一个表里面是否出现某个整数，是否出现某个字符串。

（2）映射匹配

这种匹配方式是通过某个给定的函数，把所有节点都映射到另外一种数据结构，通过比较映射后的数据结构是否完全相同，得出是否匹配的结论。

注意，这里的数据结构变换函数和散列函数不是一回事！

例如，节点类型是结构体实例，匹配方式是结构体实例内某个成员是否相等，这种其实很常用，比如各种数据库内，两个用户的身份证号相同就代表这是同一个用户。

这个例子下，数据结构变换函数是把一个用户结构体映射到其中的成员，一个存储身份证的字符串，而散列函数是以这个身份证作为输入参数，输出一个值。

再比如，判断一个字符串在一个字符串表中是否有匹配，匹配方式是两个字符串里每个字母出现的次数都相同，只是顺序不同。

这个例子下，数据结构变换函数是把一个字符串映射到一个给各个字母计数的数组，散列函数的输入值可以是字符串本身，也可以是字母计数数组。

2，字符串

可以把字符串映射成一个进制数，例如字符串“bcf”，可以映射成125，也可以映射为521

当然，映射成10进制是个非常差的选择，如果是26个小写字母组成的字符串，至少要26进制才合理，而且最好选择素数。

通过判断2个字符串的散列值是否相等，可以判断2个字符串是否相同，比如力扣 214. 最短回文串中，用来判断一个字符串是不是回文串。

3，矩阵

和字符串类似，通过把2个矩阵映射成2个列向量，判断列向量是否相等，即可判断2个矩阵是否相等。

比如 51Nod – 1140 矩阵相乘结果的判断中，用来快速判断矩阵A*B是否等于C

4，双哈希

RabinKarp子串匹配

八，OJ实战

POJ 1971 Parallelogram Counting

题目：

Description

There are n distinct points in the plane, given by their integer coordinates. Find the number of parallelograms whose vertices lie on these points. In other words, find the number of 4-element subsets of these points that can be written as {A, B, C, D} such that AB || CD, and BC || AD. No four points are in a straight line.

Input

The first line of the input contains a single integer t (1 <= t <= 10), the number of test cases. It is followed by the input data for each test case.
The first line of each test case contains an integer n (1 <= n <= 1000). Each of the next n lines, contains 2 space-separated integers x and y (the coordinates of a point) with magnitude (absolute value) of no more than 1000000000.

Output

Output should contain t lines.
Line i contains an integer showing the number of the parallelograms as described above for test case i.

Sample Input

Sample Output

5
6

这个题目，首先是平行四边形的性质。

A+D=B+C，这里的ABCD可以理解为向量，或者复数。

还可以理解为，关于坐标的线性函数，比如x+y，3x+5y这种。

本题中，为了用不同的整数表示不同的点，我用的是2000000002x+y（因为x和y有正负）

这样的数，大小约为-4*10^18到4*10^18，sum的大小约为-8*10^18到8*10^18

在sum的初始化的时候，我设置为0x7f7f7f7f7f7f7f7f，约为9*10^18，大于sum最大值。

代码：

#include<iostream>
#include<algorithm>
#include<string.h>
using namespace std;

long long h=1000000000;
long long list[1001];
long long sum[1000000];
long long x, y;

int main()
{	
	int t, n;	
	cin >> t;
	while (t--)
	{
		cin >> n;
		for (int i = 0; i < n; i++)
		{
			cin >> x >> y;
			list[i] = x*(h * 2 + 2) + y;	//点到整数的哈希
		}
		memset(sum, 0x80, sizeof(sum));
		for (int i = 0; i < n; i++)for (int j = i+1; j < n; j++)
			sum[i*n + j] = list[i] + list[j];	//数组选2个数求和的哈希
		sort(sum, sum + n*n);
		int ii = 0;
		while (sum[ii] == 0x8080808080808080)ii++;
		int num = 0, sumnum = 0;
		for (; ii < n*n; ii++)
		{
			if (sum[ii] == sum[ii - 1])num++;
			else
			{
				sumnum += num*(num + 1) / 2;
				num = 0;
			}
		}
		cout << sumnum << endl;
	}
	return 0;
}

力扣 242. 有效的字母异位词

给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。

示例 1:

输入: s = “anagram”, t = “nagaram”
输出: true
示例 2:

输入: s = “rat”, t = “car”
输出: false
说明:
你可以假设字符串只包含小写字母。

思路：

可以把一个字符串映射到一个给各个字母计数的数组，通过比较两个数组是否完全相同来判断，也可以把一个字符串映射到一个整数，通过比较2个整数是否相同来判断。

前者是确定性算法，后者需要考虑散列冲突，如果散列冲突的概率比较小，OJ的题目就能通过。

代码：

int getHash(string s)
{
    int su=0;
    for(int i=0;i<s.length();i++)su+=pow(s[i]-'a'+1,5),su%=12345678;
    return su;
}

class Solution {
public:
    bool isAnagram(string s, string t) {
        return getHash(s)==getHash(t);
    }
};

力扣 214. 最短回文串

给定一个字符串 s，你可以通过在字符串前面添加字符将其转换为回文串。找到并返回可以用这种方式转换的最短回文串。

示例 1：

输入：s = “aacecaaa”
输出：”aaacecaaa”
示例 2：

输入：s = “abcd”
输出：”dcbabcd”

提示：

0 <= s.length <= 5 * 104
s 仅由小写英文字母组成

思路：

把字符串和它的反转字符串都映射到整数，如果2个整数相同，那么说明这是一个回文串。

class Solution {
public:
    string shortestPalindrome(string s) {
        if(s=="")return "";
        long long h1=0,h2=0,mi=1,m=0;
        int p1=97,p2=1000000007;
        for(int i=0;i<s.length();i++){
            h1=h1*p1+s[i]-'a',h2=h2+mi*(s[i]-'a'),mi*=p1;
            h1%=p2,h2%=p2,mi%=p2;
            if(h1==h2)m=i;
        }
        string s2=s.substr(m+1,s.length()-m-1);
        reverse(s2.begin(),s2.end());
        return s2+s;
    }
};

力扣 49. 字母异位词分组

题目：

给定一个字符串数组，将字母异位词组合在一起。字母异位词指字母相同，但排列不同的字符串。

示例:

输入: [“eat”, “tea”, “tan”, “ate”, “nat”, “bat”],
输出:
[
[“ate”,”eat”,”tea”],
[“nat”,”tan”],
[“bat”]
]
说明：

所有输入均为小写字母。
不考虑答案输出的顺序。

思路：

逐个读取字符串，如果是第一次出现，就加入到一个新列表中，如果已经出现过在某个列表中，就加入这个列表的末尾。

由于一个列表中的字符串都是一样的，所以只要和每个列表的第一个字符串比较就行了。

但是，怎么比较两个字符串呢？

思路一：

计数，统计字母出现个数，从而比较2个字符串。

代码：

class Solution {
public:
	bool issame(string s1, string s2)
	{
		int num[26] = { 0 };
		for (int i = 0; i < s1.length(); i++)num[s1[i] - 'a']++;
		for (int i = 0; i < s2.length(); i++)num[s2[i] - 'a']--;
		for (int i = 0; i < 26; i++)if (num[i])return false;
		return true;
	}
	vector<vector<string>> groupAnagrams(vector<string>& strs) {
		vector<vector<string>> ans;
		for (int i = 0; i < strs.size(); i++)
		{
			string str = strs[i];
			bool flag = true;
			for (int i = 0; flag && i < ans.size(); i++)
			{
				if (issame(ans[i][0], str))
				{
					flag = false;
					ans[i].insert(ans[i].end(), str);
				}
			}
			if (flag)
			{
				vector<string>tmp;
				tmp.insert(tmp.end(), str);
				ans.insert(ans.end(), tmp);
			}
		}
		return ans;
	}
};

在最后一个用例超时了。

思路二：

把一个字符串映射到一个整数，比较两个字符串是否一样时只看是不是一个整数就行了。

同时，把每次映射的整数存到map里面，就不用一个个找，可以直接找到下标。

代码：

class Solution {
public:
	int change(string s)
	{
		int num[26] = { 0 }, ans = 0;
		long long k = 12345;
		for (int i = 0; i < s.length(); i++)num[s[i] - 'a']++;
		for (int i = 0; i < 26; i++)ans += num[i] * k, k = (k*k + 1) % 1234567890;
		return ans;
	}
	vector<vector<string>> groupAnagrams(vector<string>& strs) {
		vector<vector<string>> ans;
		map<int, int>m;
		int k = 0;
		for (int i = 0; i < strs.size(); i++)
		{
			int x = change(strs[i]);
			if (m[x]==0)
			{
				m[x] = ++k;
				vector<string>tmp;
				tmp.insert(tmp.end(), strs[i]);
				ans.insert(ans.end(), tmp);
			}
			else
			{
				ans[m[x]-1].insert(ans[m[x]-1].end(), strs[i]);
			}
		}
		return ans;
	}
};

思路三：

直接用数组作为key

class Solution {
public:
	vector<int> change(string s)
	{
		vector<int> num(26,0);
		for (int i = 0; i < s.length(); i++)num[s[i] - 'a']++;
		return num;
	}
	vector<vector<string>> groupAnagrams(vector<string>& strs) {
		vector<vector<string>> ans;
		map<vector<int>, int>m;
		int k = 0;
		for (int i = 0; i < strs.size(); i++)
		{
			auto x = change(strs[i]);
			if (m[x]==0)
			{
				m[x] = ++k;
				vector<string>tmp;
				tmp.insert(tmp.end(), strs[i]);
				ans.insert(ans.end(), tmp);
			}
			else
			{
				ans[m[x]-1].insert(ans[m[x]-1].end(), strs[i]);
			}
		}
		return ans;
	}
};

剑指 Offer II 032. 有效的变位词

给定两个字符串 s 和 t ，编写一个函数来判断它们是不是一组变位词（字母异位词）。

注意：若 s 和 t 中每个字符出现的次数都相同且字符顺序不完全相同，则称 s 和 t 互为变位词（字母异位词）。