乘积最大的连续子序列_求数组中最大连续子序列的和

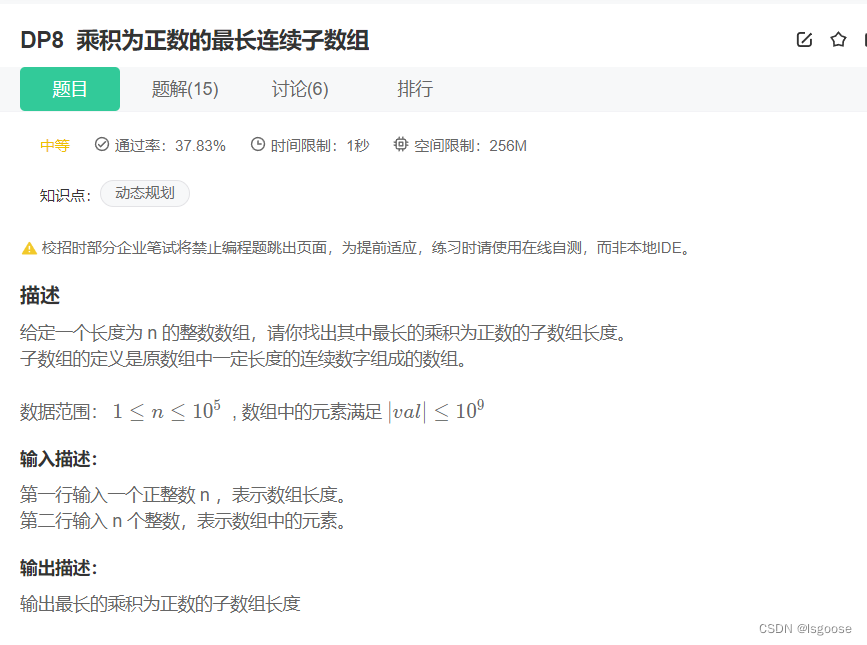
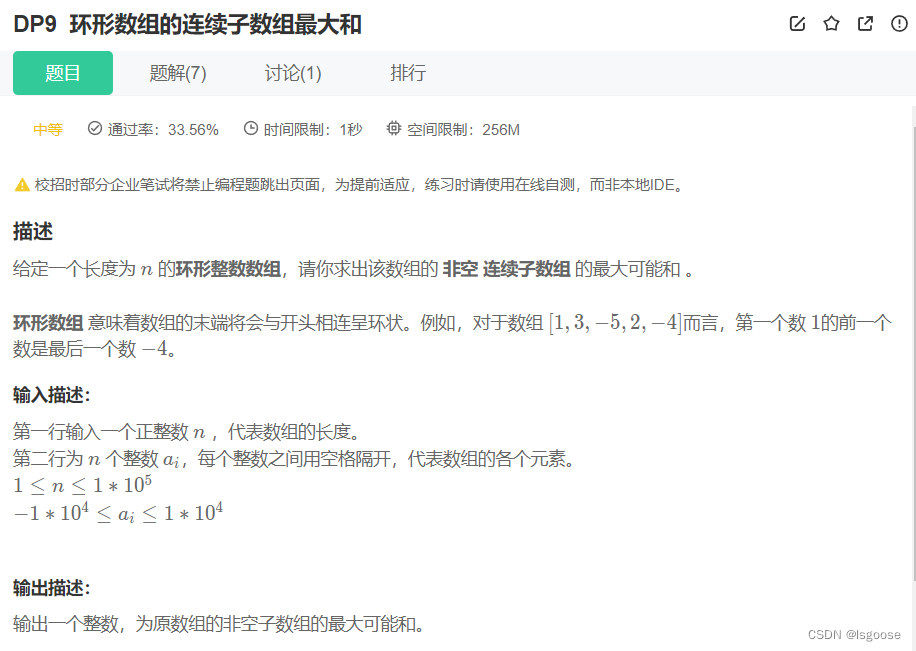
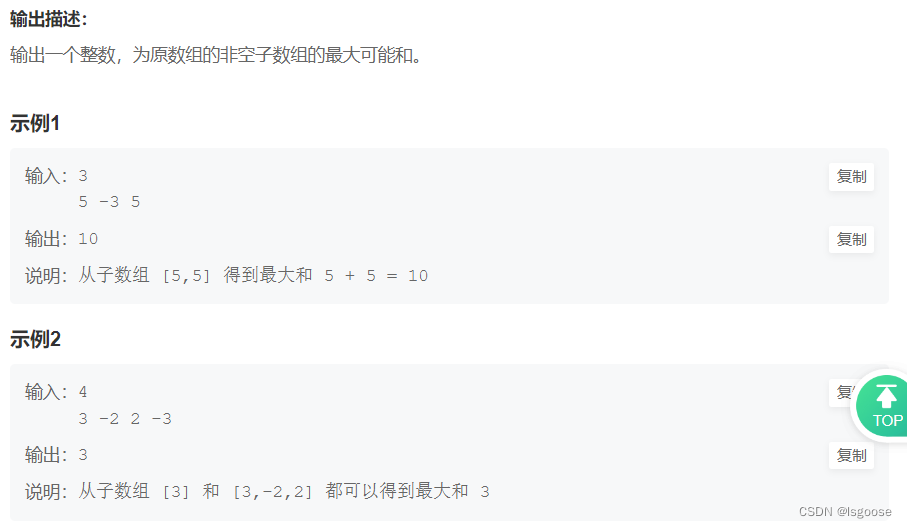
1.非环形

 注意审题！！

这里是求连续最长乘积为正数的长度是多少，我们维护两个长度，一个pos一个neg，pos代表到当前这个数为止的最长正数乘积，neg代表到当前这个数为止的最长负数乘积，我们对每个数进行如下操作:

1.若当前数为正，则最长的正数序列长度可以加一，若有最长负数序列，则也加一

2.若当前数为0，则所有以此数结尾的序列最长正数和负数序列都为0，故全部更新为0

3.若当前数为负，则需要交换pos和neg

具体代码如下所示：

#include<bits/stdc++.h>
using namespace std;
int dp(vector<int> &nums){
    int res=0;
    int pos=nums[0]>0 ? 1: 0;
    int neg=nums[0]<0 ? 1: 0;
    for(int i=1;i<nums.size();++i){
        if(nums[i]>0){
            pos=pos+1;
            neg=neg>0 ? neg+1 : 0;
        }else if(nums[i]==0){
            pos=neg=0;
        }else{
            int tmp=neg>0 ? neg+1:0;
            neg=pos+1;
            pos=tmp;
        }
        res=max(res,pos);
    }
    return res;
}

int main(){
    int n;
    cin>>n;
    vector<int> nums(n);
    for(int i=0;i<n;++i){
        cin>>nums[i];
    }
    cout<<dp(nums)<<endl;
    return 0;
}

2.环形数组

 这里的思路参考了牛客里边的答案。

首先，我们都知道如何去求非循环数组的最大和，就是一遍线性dp，每次更新以当前数作为结尾的最大长度，那么如果是循环的呢？我们每次用一个新的起点来一次线性dp就可以求出。

具体代码如下所示：

#include<bits/stdc++.h>//超时的代码
using namespace std;
int solve(int n, vector<int> &v, vector<int> &dp);
int process2(int start, vector<int>&v);
int main(){
    int n;
    cin>>n;
    vector<int> v(n);
    for (int i = 0; i < n; ++i){
        scanf("%d",&v[i]);
    }
    vector<int> dp(n, INT_MIN);
    cout<<solve(n,v, dp)<<endl;
    return 0;
}
int solve(int n, vector<int> &v, vector<int> &dp){
    int ans = process2(0, v);
    for(int i = 1; i < n; ++i){
        ans = max(ans,process2(i,v));
    }
    return ans;
}
int process2(int start, vector<int>&v){
    int ans = v[start];
    for(int i = 1; i < v.size(); ++i){
        ans = max(ans+v[(start + i)%v.size()],v[(start+i)%v.size()]);
    }
    return ans;
}

这样的时间复杂度是O(n^2)，会超时。

• 切换看法，按照普通最大连续和的思路，即在dp的过程中可以得到最大的连续子数组和。
• 同理，如果再求一个最小的连续子数组和，就会发现一个特性。
• 假设用sum记录整个数组的和，那么最大连续子数组和dpmax 和最小连续子数组dpmin和一定是相连的两部分，因为假设不想连，中间这一段要么大于0，那么它应该属于最大子数组连续和，否则它应该属于最小连续子数组和。
• 故最后求得sum，dpmax，dpmin以后就可以进行判定。假设dpmax+dpmin<sum这说明数组两边的端点之和是正值，故应该把这一部分留给(dpmax=sum−dpmin)，否则直接返回dpmax即可，当然这里有一个特例（在初始化dpmax的时候给予了数组的第一个值v[0]，如果其是负数，则必定有dpmax+dpmin<sum 故此处应该特判，如果dpmax<0直接返回即可）

思路如下所示：
1.有环情况：先求出无环情况下连续子数组的最小值 res2，然后用数组和 sum 减去最小值 res2 即为环形情况下的连续子数组最大值
2.无环情况：最大子数组和
3.最大的环形子数组和 = max(最大子数组和，数组总和-最小子数组和),要排除全负数情况=最大子数组和
原文链接：https://blog.csdn.net/qq_35915636/article/details/123974337

#include<bits/stdc++.h>
using namespace std;
int dp(vector<int> &nums){
    int sum, dpmx, dpmn, mx, mn;
    dpmx=dpmn=mx=mn=sum=nums[0];
    for(int i=1;i<nums.size();++i){
        mx=max(mx+nums[i],nums[i]);
        mn=min(mn+nums[i],nums[i]);
        dpmx=max(dpmx, mx);
        dpmn=min(dpmn, mn);
        sum+=nums[i];
    }
    if(dpmx<0) return dpmx;
    if(dpmx+dpmn<sum) dpmx=sum-dpmn;
    return dpmx;
}

int main(){
    int n;
    cin>>n;
    vector<int> nums(n);
    for(int i=0;i<n;++i){
        cin>>nums[i];
    }
    cout<<dp(nums)<<endl;
    return 0;
}

今天的文章乘积最大的连续子序列_求数组中最大连续子序列的和分享到此就结束了，感谢您的阅读。