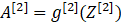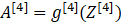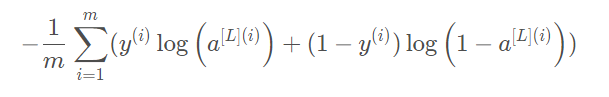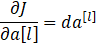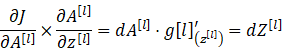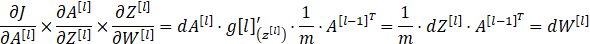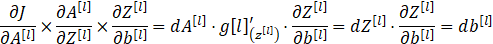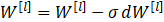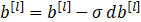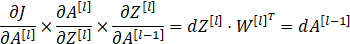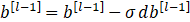神经网络正向传播和反向传播_神经网络反向传播原理

一、前言

        我在之前的博客里面介绍过浅层的神经网络，现在就从浅层神经网络出发，介绍深度神经网络（DNN）的正向传播和反向传播。希望网友们看本博客之前需要对神经网络有个简单的了解，或者可以看博客初探神经网络（深度学习入门）进行了解学习。

        本文将结合吴恩达的视频、作业及其个人的理解进行写作，如有不对的地方，还望指正。 

二、DNN的模型

        神经网络有一个输入层、多个隐含层和一个输出层组成。每个隐含层都执行了线性操作和激活函数操作。

三、DNN的前向传播

（1）DNN前向传播的数学基础

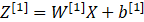
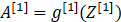
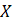
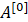
        第一层需要计算   , （ 可以看做 ）

        第二层需要计算 ，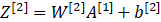

        以此类推，

        第四层为 ，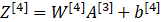

        前向传播可以归纳为多次迭代 ， 。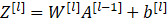

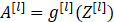
        成本函数 ：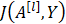

       其中，m是指样本数。Z是指线性计算，A是指激活函数计算的结果

（2）DNN前向传播的代码实现

       前向传播有以下三个步骤

• LINEAR
• LINEAR – >ACTIVATION，其中激活函数将会使用ReLU或Sigmoid。
• [LINEAR – > RELU] ×（L-1） – > LINEAR – > SIGMOID（整个模型） 

        2.1线性计算部分 

# GRADED FUNCTION: linear_forward 线性传播 def linear_forward(A, W, b): """ 实现正向传播的线性部分。 Arguments: A -- 来自上一层（或输入数据）的激活，维度为(上一层的节点数量，示例的数量） W -- 权重矩阵，numpy数组，维度为（当前图层的节点数量，前一图层的节点数量 b -- 偏向量，numpy向量，维度为（当前图层节点数量，1） Returns: Z -- 激活功能的输入，也称为预激活参数 cache -- 一个包含“A”，“W”和“b”的字典，存储这些变量以有效地计算后向传递 """ ### START CODE HERE ### (≈ 1 line of code) Z = np.dot(W,A)+b ### END CODE HERE ### assert(Z.shape == (W.shape[0], A.shape[1])) cache = (A, W, b) return Z, cache

        2.2线性激活部分 

        激活函数有许多种，在我之前的博客里也都有讲过。下面先简单写下Relu和sigmoid激活函数。

import numpy as np def sigmoid(Z): """ Implements the sigmoid activation in numpy Arguments: Z -- numpy array of any shape Returns: A -- output of sigmoid(z), same shape as Z cache -- returns Z as well, useful during backpropagation """ A = 1/(1+np.exp(-Z)) cache = Z return A, cache def relu(Z): """ Implement the RELU function. Arguments: Z -- Output of the linear layer, of any shape Returns: A -- Post-activation parameter, of the same shape as Z cache -- a python dictionary containing "A" ; stored for computing the backward pass efficiently """ A = np.maximum(0,Z) assert(A.shape == Z.shape) cache = Z return A, cache 

         计算激活函数

def linear_activation_forward(A_prev,W,b,activation): """ 实现LINEAR-> ACTIVATION 这一层的前向传播 参数： A_prev - 来自上一层（或输入层）的激活，维度为(上一层的节点数量，示例数） W - 权重矩阵，numpy数组，维度为（当前层的节点数量，前一层的大小） b - 偏向量，numpy阵列，维度为（当前层的节点数量，1） activation - 选择在此层中使用的激活函数名，字符串类型，【"sigmoid" | "relu"】 返回： A - 激活函数的输出，也称为激活后的值 cache - 一个包含“linear_cache”和“activation_cache”的字典，我们需要存储它以有效地计算后向传递 """ if activation == "sigmoid": Z, linear_cache = linear_forward(A_prev, W, b) A, activation_cache = sigmoid(Z) elif activation == "relu": Z, linear_cache = linear_forward(A_prev, W, b) A, activation_cache = relu(Z) assert(A.shape == (W.shape[0],A_prev.shape[1])) cache = (linear_cache,activation_cache) return A,cache 

        2.3计算成本函数

def compute_cost(AL,Y): """ 实施等式（4）定义的成本函数。 参数： AL - 与标签预测相对应的概率向量，维度为（1，示例数量） Y - 标签向量（例如：如果不是猫，则为0，如果是猫则为1），维度为（1，数量） 返回： cost - 交叉熵成本 """ m = Y.shape[1] cost = -np.sum(np.multiply(np.log(AL),Y) + np.multiply(np.log(1 - AL), 1 - Y)) / m cost = np.squeeze(cost) assert(cost.shape == ()) return cost 

 四、DNN反向传播

（1）DNN反向传播的数学基础

         反向传播是神经网络中非常重要的一部分，而反向传播其实也是很简单的内容，其核心就是我们数学微积分中的求导链式法则，只要掌握了这个链式法则，就能一直往前传播，对参数W和b进行更新。接下来我们根据三（1）中DNN正向传播中的公式，分别计算第l层和第l-1层的反向传播，以此为例不断向前进行传播。

第l层：   

第l-1层：

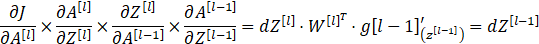
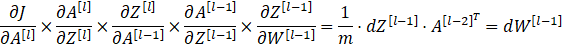
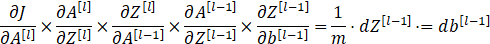
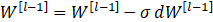
依次类推进行反向传播

（2）DNN反向传播的代码实现

          实现后向传播线性部分

def linear_backward(dZ,cache): """ 为单层实现反向传播的线性部分（第L层） 参数： dZ - 相对于（当前第l层的）线性输出的成本梯度 cache - 来自当前层前向传播的值的元组（A_prev，W，b） 返回： dA_prev - 相对于激活（前一层l-1）的成本梯度，与A_prev维度相同 dW - 相对于W（当前层l）的成本梯度，与W的维度相同 db - 相对于b（当前层l）的成本梯度，与b维度相同 """ A_prev, W, b = cache m = A_prev.shape[1] dW = np.dot(dZ, A_prev.T) / m db = np.sum(dZ, axis=1, keepdims=True) / m dA_prev = np.dot(W.T, dZ) assert (dA_prev.shape == A_prev.shape) assert (dW.shape == W.shape) assert (db.shape == b.shape) return dA_prev, dW, db 

         实现后向线性激活

def linear_activation_backward(dA,cache,activation="relu"): """ 实现LINEAR-> ACTIVATION层的后向传播。 参数： dA - 当前层l的激活后的梯度值 cache - 我们存储的用于有效计算反向传播的值的元组（值为linear_cache，activation_cache） activation - 要在此层中使用的激活函数名，字符串类型，【"sigmoid" | "relu"】 返回： dA_prev - 相对于激活（前一层l-1）的成本梯度值，与A_prev维度相同 dW - 相对于W（当前层l）的成本梯度值，与W的维度相同 db - 相对于b（当前层l）的成本梯度值，与b的维度相同 """ linear_cache, activation_cache = cache if activation == "relu": dZ = relu_backward(dA, activation_cache) dA_prev, dW, db = linear_backward(dZ, linear_cache) elif activation == "sigmoid": dZ = sigmoid_backward(dA, activation_cache) dA_prev, dW, db = linear_backward(dZ, linear_cache) return dA_prev,dW,db 

        实现参数更新 

def update_parameters(parameters, grads, learning_rate): """ 使用梯度下降更新参数 参数： parameters - 包含你的参数的字典 grads - 包含梯度值的字典，是L_model_backward的输出 返回： parameters - 包含更新参数的字典 参数[“W”+ str（l）] = ... 参数[“b”+ str（l）] = ... """ L = len(parameters) // 2 #整除 for l in range(L): parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)] parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)] return parameters 

五、其他

        可能有部分人看完本博客后还是对DNN的正向传播和反向传播不是特别明白，这里有两个选择给大家。第一就是DNN的前向传播是很容易理解的，我们理解完这个就行了，接下来的交给tensorflow等深度学习框架搞定吧，第二种选择就是把吴恩达这部分的作业自己独立完成一遍。下面附上链接。

链接：https://pan.baidu.com/s/1WUFCM3R77bnk960Sw_9OLA 
提取码：9sl2 
 

今天的文章
神经网络正向传播和反向传播_神经网络反向传播原理分享到此就结束了，感谢您的阅读。