学习笔记|生成对抗网络（Generative Adversarial Networks,GAN）——让机器学习具有创造力

1.生成对抗网络概述

有时候我们希望网络具有一定的创造力，比如画画、编曲等等，能否实现呢？是可以实现的，大家可以鉴别一下下面这几张照片，哪些是真实的人脸，哪些是机器生成的人脸。很难判断吧？本节最后会给出答案。

要实现上述能力，就要用到一种新的网络架构— 生成对抗网络（Generative Adversarial Net，GAN
） 。首先，我们大概来了解一下什么是 “生成” ，什么是 “对抗”。

1.1 对“生成”的理解

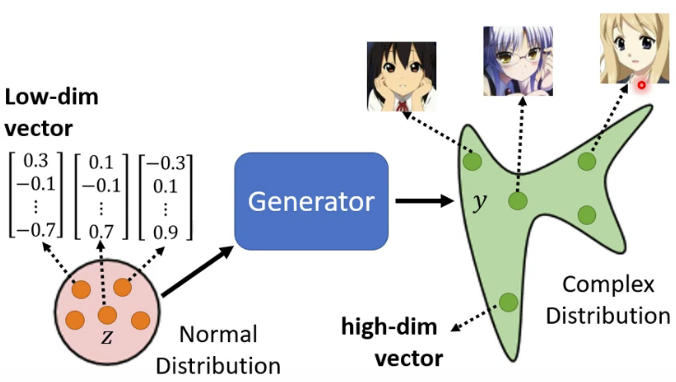
假设我们设计一个网络，将其称为 “生成器（Generator）”。生成器的输入是一个向量$z$，该向量一般是低维向量，它是通过一个特定的分布采样出来的，例如正态分布。生成器的输出是另一个向量$y$，该向量是一个高维向量，比如一个二次元的人脸。由于生成器的输入向量是通过一个分布随机采样的，所以输入向量每次都是不一样的，因此生成器每次的输出也是不一样的，会形成一个复杂的分布。尽管输出向量不一样，但是我们要求这些输出向量都是二次元的人脸，而不是其它。也就是说期望生成器输出的复杂分布要和某个特定分布（例如所有二次元人脸的集合）尽可能相似，如何做到呢？这就要用到“对抗”。

1.2 对“对抗”的理解

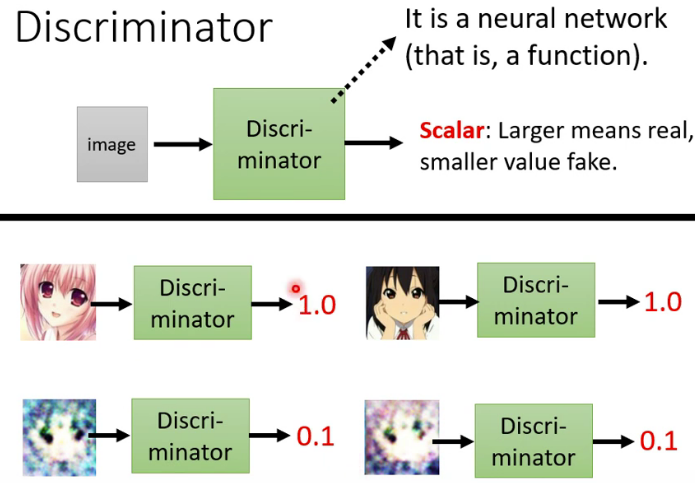
我们常说要“感谢对手”，为什么呢？因为对手逼得我们不断想办法进步，最后让我们进化成长为优秀的人。为了使生成网络不断进化以成为画画高手，我们还需要训练另外一个网络，叫做 “鉴别器（Discriminator）” 。鉴别器是专门用来和生成网络进行对抗的，就是用它来逼得生成网络不断进化。鉴别器的输入是一张图片，它的输出则是一个0-1的数字，数字越大就越认为这张图片是一个二次元图片，数字越小呢就越认为这张图片不是一个二次元图片。比如下图中上面两张图片很清楚是二次元，所以鉴别器输出1.0，而下面两张图片很模糊，所以鉴别器输出0.1。因此，简单点讲，鉴别器的功能就是判断某张图片到底是不是二次元图片。

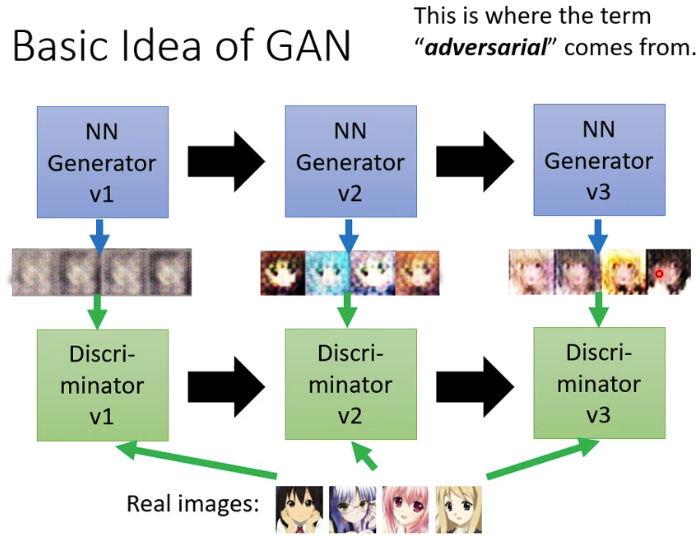
现在我们把这个鉴别器拿过来和生成器进行对抗：

• ①版本1的生成器的参数是随机生成的，所以其生成的图片啥都不是。这 时候，我们对鉴别器进行训练，以使鉴别器能够鉴别出哪些是生成器生成的图片，哪些是真实的二次元人脸。经过训练后，我们得到了版本1的鉴别器。
• ②在版本1的鉴别器的基础上，我们再来训练生成器，训练的目的是让鉴别器分辨不出哪些是生成器生成的图片，哪些是真实的二次元人脸。通过训练之后，得到了版本2的生成器，此时生成的图片有一点点像二次元了，足以骗过版本1的鉴别器。
• ③在版本2的生成器的基础上，我们接着训练鉴别器，同样是要使鉴别器能够鉴别出哪些是版本2生成器生成的图片，哪些是真实的二次元人脸。通过训练之后，得到了版本2的鉴别器。
• ④重复上述过程，不断进化生成器和鉴别器，最后生成器可以生成非常逼真的二次元人脸。

通过上述过程我们可以看出，生成器和鉴别器在不断的对抗过程中，两者都在不断的进步，可以说是对抗成就了对方。所以，它们亦敌亦友，相爱相杀，既对立又统一。

2. 生成对抗网络的理论基础

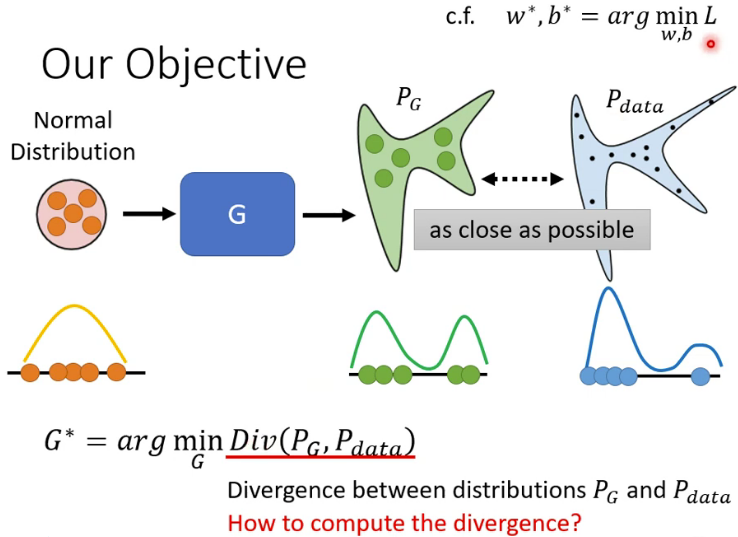
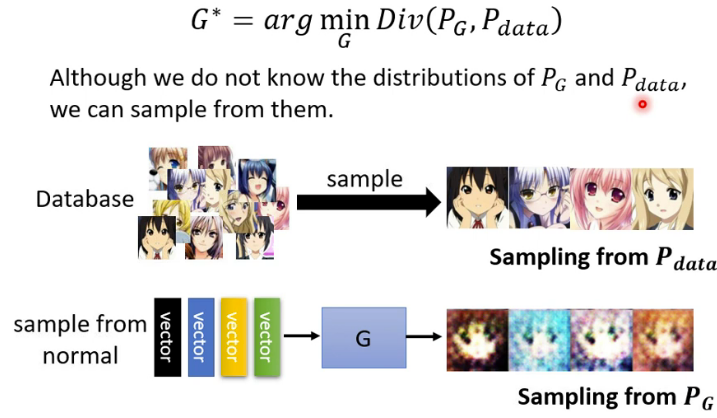
我们刚才提到生成器的输入是由一个简单的分布（如正态分布）采样得到的一堆向量，输出是一堆向量构成另一个一个复杂的分布，用$P_G$表示。我们期望$P_G$和某个特定的分布尽可能地相似，而这个分布来自于一堆真实的数据，这个分布表示为$P_{data}$。如果我们用$Div(P_G,P_{data})$来表示这两个分布的Divergence(这个英文不好翻译，暂且理解为“差异程度”吧），那么我们的目标就是寻找一个生成器$G^{\ast }$要使$Div(P_G,P_{data})$最小，即，$$G^{\ast }=arg\underset{G}{\min }Div(P_G,P_{data})$$我们知道在机器学习中，训练的目标是要使损失函数最小，所以在该任务中损失函数就是$Div(P_G,P_{data})$。但是有一个很关键的问题，我们如何计算这两个分布的Divergence呢？好像没法用解析式去描述这两个分布的Divergence，那怎么办呢？我们可以通过采样的方式来计算这两个分布的Divergence。

采样是很好办的，以二次元人脸生成器为例。$P_{data}$的采样很简单，我们从一堆二次元的图库中随机采样一些图片就行了。$P_G$的采样也很简单，我们从正态分布中采样一些向量，生成器输出一些图片，就得到$P_G$的采样图片了。我们有了$P_{data}$和$P_G$的采样了，那么怎么计算$Div(P_G,P_{data})$呢？这就需要用到鉴别器了。

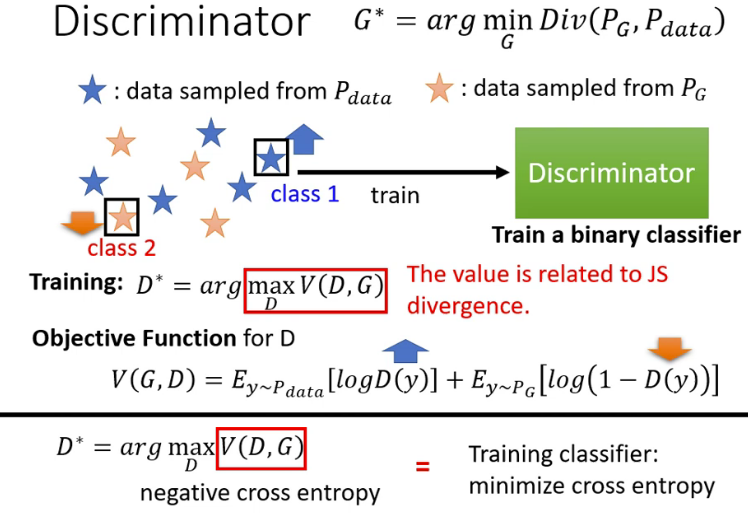
假设从$P_{data}$采样得到的数据用蓝色五角星表示，从$P_G$采样得到的数据用黄色五角星表示。鉴别器的目的就是遇到蓝色五角星时输出的分数要尽量高，遇到黄色五角星时输出的分数要尽量低。如果用$V(D,G)$鉴别器训练的目标函数(最大化一般称为目标函数，最小化一般称为损失函数)，那么就有，$$V(G,D)=E_{y\sim P_{\text{data }}}[\log D(y)]+E_{y\sim P_G}[\log (1-D(y))]$$其中$E_{y\sim P_{\text{data }}}[\log D(y)]$表示当$y$从$P_{data}$中采样，通过鉴别器后的输出$D(y)$要尽可能大，$E_{y\sim P_G}[\log (1-D(y))]$表示当$y$从$P_{data}$中采样，通过鉴别器后的输出$D(y)$要尽可能小，因此加了个负号。可以看出该式中还专门取了个对数，这是为了和分类问题中的交叉熵保持一致，因为该式加个负号就是分类问题中的交叉熵了。在训练分类器的时候是要最小化交叉熵，这里要最大化$V(D,G)$，所以两者是等同的。因此，鉴别器也可以看成一个二分类器，一类数据从$P_{data}$采样得到，一类数据$P_G$采样得到。
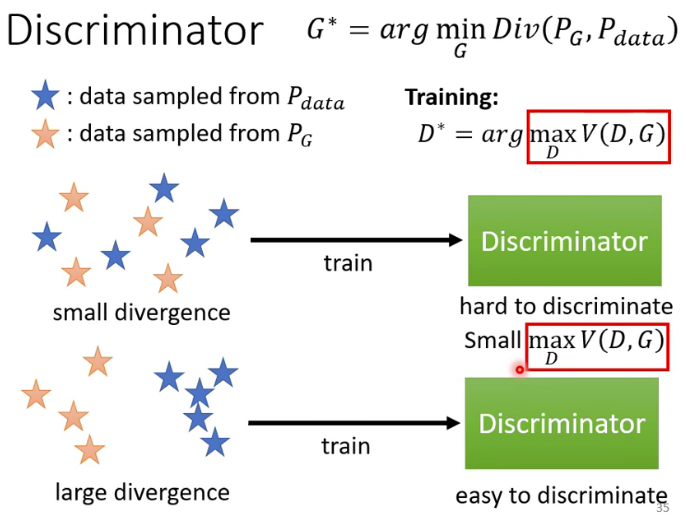
最重要的一点是，${\max }_{D}V(D,G)$和上面提到的Divergence是相关的，这一点在GAN最原始的文章中有严格的数学推理。

我们可以从直观上来理解为什么${\max }_{D}V(D,G)$和$Div(P_G,P_{data})$是相关的。假设$Div(P_G,P_{data})$比较小，表示这两者很相似，那么从$P_G$和$P_{data}$采样得到的数据混到一起就很难被鉴别，因此鉴别器的${\max }_{D}V(D,G)$就不会太大；相反地，如果$Div(P_G,P_{data})$比较大，表示这两者差异性很大，那么从$P_G$和$P_{data}$采样得到的数据混到一起就比较容易被鉴别，因此鉴别器的${\max }_{D}V(D,G)$就会比较大。希望了解详情的，请移步GAN的原文。

既然我们已经知道${\max }_{D}V(D,G)$和$Div(P_G,P_{data})$是相关的，而且是正相关的。所以生成器的损失函数中的$Div(P_G,P_{data})$就可以用${\max }_{D}V(D,G)$来进行替换，可以得到，$$G^{\ast }=arg\underset{G}{\min }\underset{D}{\max }V(D,G)$$这个损失函数有点复杂，又是$\min$，又是$\max$。其实这个损失函数包含了两个优化问题：首先是在固定生成器$G$的情况下，找到一个鉴别器$G$使$V(D,G)$最大，然后是要找到鉴别器$G$，使${\max }_{D}V(D,G)$最小。因此，前面提到的对抗过程就是求解$G^{\ast }=arg{\min }_G{\max }_{D}V(D,G)$的过程。所以生成对抗网络的训练如下图所示。

对了，本节最前面的人脸全部是由机器生成的，惊叹吧！？

今天的文章
学习笔记|生成对抗网络（Generative Adversarial Networks,GAN）——让机器学习具有创造力分享到此就结束了，感谢您的阅读。