样条曲线算法_python绘制光滑曲线图

样条曲线

所谓(Spline Curves)是指给定一组控制点而得到一条曲线，曲线的大致形状由这些点予以控制，一般可分为插值样条和逼近样条两种，插值样条通常用于数字化绘图或动画的设计，逼近样条一般用来构造物体的表面。

定义

样条曲线是经过一系列给定点的光滑曲线。最初，样条曲线都是借助于物理样条得到的，放样员把富有弹性的细木条（或有机玻璃条），用压铁固定在曲线应该通过的给定型值点处，样条做自然弯曲所绘制出来的曲线就是样条曲线。样条曲线不仅通过各有序型值点，并且在各型值点处的一阶和二阶导数连续，也即该曲线具有连续的、曲率变化均匀的特点。

样条曲线——非均匀有理 B 样条曲线

非均匀有理 B 样条曲线（NURBS），是一种用途广泛的样条曲线，它不仅能够用于描述自由曲线和曲面，而且还提供了包括能精确表达圆锥曲线曲面在内各种几何体的统一表达式。自1983年，SDRC公司成功地将NURBS模型应用在它的实体造型软件中，NURBS已经成为计算机辅助设计及计算机辅助制造的几何造型基础，得到了广泛应用 [1]  。

AutoCAD 使用的就是这种NURBS数学模型来创建样条曲线，这也是在MDT中进行曲面造型和实体造型的基础。

在详细阐明AutoCAD用于构造和修改NURBS曲线（以下简称“样条曲线”）的各项功能之前，从数学和几何角度了解关于NURBS曲线的几个术语，是非常有必要的。这里仅解释与理解AutoCAD中的NURBS曲线有关的名词，其它相关详细数学知识，请参见有关资料。

NURBS曲线的相关术语

型值点或拟合点：所求的样条曲线应通过的已知给定点。

特征多边形或控制多边形：样条曲线是由一些折线组成的多边形构造出来的。简单地说，以数值计算的方法，用光滑的参数曲线段逼近该折线多边形，就构造出一条样条曲线。改变该多边形的顶点和个数，会影响曲线的形状。这里所说的折线多边形，就是样条曲线的特征多边形或控制多边形 [2]  。

样条曲线曲线相关性质

样条曲线曲线段

样条曲线是由一组逼近控制多边形的光滑参数曲线段构成，这些曲线段就是样条曲线段。

特征多边形/控制多边形的顶点/控制点

构成特征多边形的各段折线的端点，就是特征多边形的顶点，也叫做控制多边形的控制点。只有在特殊情况下，样条曲线才能通过控制点。

样条曲线曲线次数

样条曲线的次数，是由样条曲线数学定义中所取的基函数所决定的。直观的说，所构成样条曲线的一段光滑参数曲线段，由控制多边形的相邻连续的几段折线段决定，就是几次样条，最常用的就是二次和三次样条。二次样条的某一曲线段只与相应的两段折线段，三个控制多边形顶点有关，改变其中一个顶点，将影响三段样条曲线段。同样的，对三次样条，某一曲线段由相应的三段折线段，四个控制点决定 [2]  。

样条曲线曲线阶数

阶数与次数有关，样条曲线的阶是其次数加一。阶数越高，控制点越多。二次样条的阶数是三，样条曲线段由三个控制点决定；三次样条的阶数是四，样条曲线段与四个控制点决定。

样条曲线曲线权值

权值可控制样条曲线段在控制多边形范围内做局部调整，反映了曲线靠近控制多边形的程度，权值越大，曲线段越靠近控制多边形。反之，则远离。当权值为1时，NURBS曲线退化为非有理B样条曲线，可见非有理B样条曲线是NURBS的一个子集。

样条曲线曲线允差

允差是指样条曲线通过型值点的精确程度，允差越小，样条曲线与型值点越接近，允差为零，样条曲线将通过型值点 [3]  。

样条曲线曲线产生方法

编辑

AutoCAD用 SPLINE 命令创建样条曲线即 NURBS 曲线。还提供用 splinedit 命令，平滑多段线（POLYLINE）拟合生成近似样条曲线，以下称为“样条拟合多段线”。这种曲线不是真正意义上的样条曲线，而是由若干直线（曲线）段构成的多段线，逼近于样条曲线。但使用 SPLINE 命令可把这种二维和三维样条拟合多段线转换为样条曲线。

用SPLINE命令创建的样条曲线和编辑平滑多段线生成的样条拟合多段线相比，有以下不同：

样条曲线显然要比样条拟合多段线精确的多。在工程应用中，样条拟合多段线不能作为数学分析的基础，不能在曲线上，生成切线、法线或提取曲线上的点位数据。

在以下样例中（图1），样条曲线用于创建混凝土人行道的亮显边界 [4]  。

样条函数

在数学学科数值分析中，样条是一种特殊的函数，由多项式分段定义。样条的英语单词spline来源于可变形的样条工具，那是一种在造船和工程制图时用来画出光滑形状的工具。在中国大陆，早期曾经被称做“齿函数”。后来因为工程学术语中“放样”一词而得名。

在插值问题中，样条插值通常比多项式插值好用。用低阶的样条插值能产生和高阶的多项式插值类似的效果，并且可以避免被称为龙格现象的数值不稳定的出现。并且低阶的样条插值还具有“保凸”的重要性质。

在计算机科学的计算机辅助设计和计算机图形学中，样条通常是指分段定义的多项式参数曲线。由于样条构造简单，使用方便，拟合准确，并能近似曲线拟合和交互式曲线设计中复杂的形状，样条是这些领域中曲线的常用表示方法。

定义

给定k个点ti，称为节点（knot），分布在一个区间[a,b]满足

一个参数曲线

称为n次样条，如果

并且在限制到每个子区间时，

换句话说，在每个子区间或者说节点长度（knot span）

S和一个n次多项式相同。

S（ti） 称为节点值而（ti,S（ti））称为内部控制点（internal control point）. (t0,…,tk-1)称为节点向量。如果节点等距分布在区间[a,b]上，我们称样条均匀（uniform），否则为非均匀（non-uniform）。 [1] 

样条函数举例

最简单的样条是一次的，它也叫做线性样条，或者多边形。一般的样条是自然的三次样条。自然定义为样条多项式的二阶导数在插值区域的两端相等。

在区间

，这使得样条在插值区间外为直线而不影响光滑程度。 [1] 

样条函数注解

对于一个给定的节点向量，所有n次样条构成一个向量空间。这个空间的一个基是n次B样条基。 [1] 

样条函数历史

在计算机被使用之前，数字演算用手工完成。虽然分段定义的象signum函数或阶梯函数这样的函数也被用到，一般人更喜欢多项式因为它们比较容易算。随着计算机的发展，样条变得越来越重要。它们一开始是作为多项式在插值中的替代品，后来又作为在计算机图形学中构造光滑和可变形状的工具。

spline function是一类分段（片）光滑、并且在各段交接处也有一定光滑性的函数。简称样条。样条一词来源于工程绘图人员为了将一些指定点连接成一条光顺曲线所使用的工具，即富有弹性的细木条或薄钢条。由这样的样条形成的曲线在连接点处具有连续的坡度与曲率。分段低次多项式、在分段处具有一定光滑性的函数插值就是模拟以上原理发展起来的，它克服了高次多项式插值可能出现的振荡现象，具有较好的数值稳定性和收敛性，由这种插值过程产生的函数就是多项式样条函数。

样条函数的研究始于20世纪中叶，到了60年代它与计算机辅助设计相结合，在外形设计方面得到成功的应用。样条理论已成为函数逼近的有力工具。它的应用范围也在不断扩大，不仅在数据处理、数值微分、数值积分、微分方程和积分方程数值解等数学领域有广泛的应用，而且与最优控制、变分问题、统计学、计算几何与泛函分析等学科均有密切的联系。

实现所需的库

numpy、scipy、matplotlib

实现所需的方法

插值

nearest：最邻近插值法
zero：阶梯插值
slinear：线性插值
quadratic、cubic：2、3阶B样条曲线插值

拟合和插值的区别

简单来说，插值就是根据原有数据进行填充，最后生成的曲线一定过原有点。

拟合是通过原有数据，调整曲线系数，使得曲线与已知点集的差别（最小二乘）最小，最后生成的曲线不一定经过原有点。

代码实现

# -*- coding: utf-8 -*-

# 调用模块
# 调用数组模块
import numpy as np
# 实现插值的模块
from scipy import interpolate
# 画图的模块
import matplotlib.pyplot as plt
# 生成随机数的模块
import random

# random.randint(0, 10) 生成0-10范围内的一个整型数
# y是一个数组里面有10个随机数，表示y轴的值
y = np.array([random.randint(0, 10) for _ in range(10)])
# x是一个数组，表示x轴的值
x = np.array([num for num in range(10)])

# 插值法之后的x轴值，表示从0到9间距为0.5的18个数
xnew = np.arange(0, 9, 0.5)

“””
kind方法：
nearest、zero、slinear、quadratic、cubic
实现函数func
“””
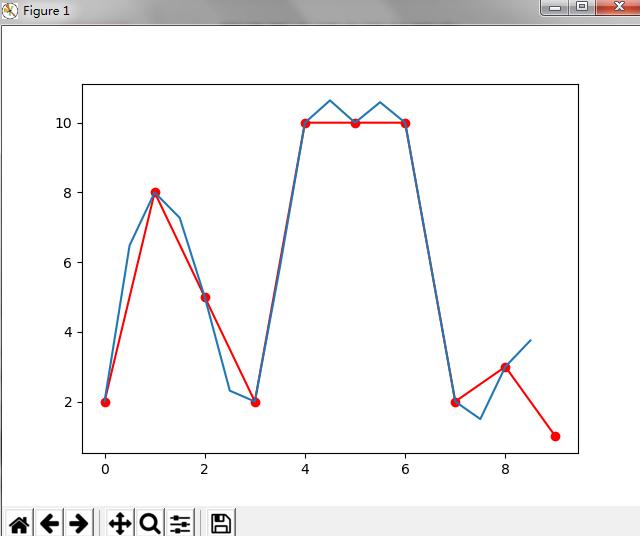
func = interpolate.interp1d(x, y, kind=’cubic’)
# 利用xnew和func函数生成ynew，xnew的数量等于ynew数量
ynew = func(xnew)

# 画图部分
# 原图
plt.plot(x, y, ‘ro-‘)
# 拟合之后的平滑曲线图
plt.plot(xnew, ynew)
plt.show()
 

今天的文章
样条曲线算法_python绘制光滑曲线图分享到此就结束了，感谢您的阅读。