向量正交:向量 u u u与向量 v v v正交 ⟺ u ⋅ v = 0 ⟺ u ⊥ v \Longleftrightarrow u\cdot v = 0\Longleftrightarrow u\bot v ⟺u⋅v=0⟺u⊥v
子空间正交:子空间S与子空间T正交 ⟺ \Longleftrightarrow ⟺S中的每个向量与T中的每个向量均正交.
基正交
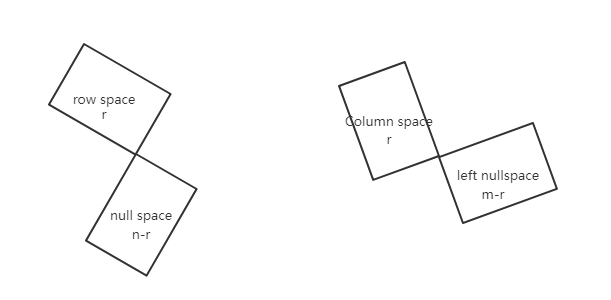
四个基本子空间的关系
左侧将 R n R^n Rn划分为两个子空间 ⟷ \longleftrightarrow ⟷行空间和零空间在 R n R^n Rn内互为正交补充1.
右侧将 R m R^m Rm划分为两个子空间 ⟷ \longleftrightarrow ⟷列空间和左零空间在 R m R^m Rm内互为正交补充.
行空间与零空间正交,列空间与 A T A^T AT的零空间正交。
零向量和任意向量正交。
-
零空间包含所有垂直于行空间的向量。 ↩︎
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/10492.html