最详细版图解优先队列（堆）

一、队列与优先队列的区别

1. 队列是一种FIFO（First-In-First-Out）先进先出的数据结构，对应于生活中的排队的场景，排在前面的人总是先通过，依次进行。
2. 优先队列是特殊的队列，从“优先”一词，可看出有“插队现象”。比如在火车站排队进站时，就会有些比较急的人来插队，他们就在前面先通过验票。优先队列至少含有两种操作的数据结构：insert（插入），即将元素插入到优先队列中（入队）；以及deleteMin（删除最小者），它的作用是找出、删除优先队列中的最小的元素（出队）。

二、优先队列（堆）的特性

• 优先队列的实现常选用二叉堆，在数据结构中，优先队列一般也是指堆。

• 堆的两个性质：

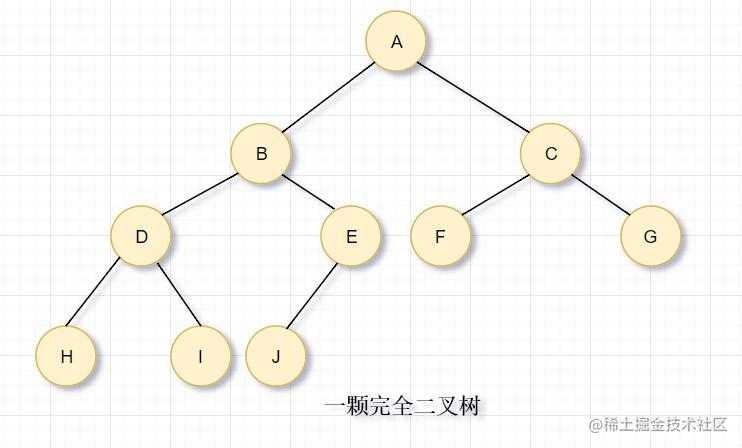
1. 结构性：堆是一颗除底层外被完全填满的二叉树，底层的节点从左到右填入，这样的树叫做完全二叉树。

2. 堆序性：由于我们想很快找出最小元，则最小元应该在根上，任意节点都小于它的后裔，这就是小顶堆（Min-Heap）；如果是查找最大元，则最大元应该在根上，任意节点都要大于它的后裔，这就是大顶堆(Max-heap)。

   结构性：

   

通过观察发现，完全二叉树可以直接使用一个数组表示而不需要使用其他数据结构。所以我们只需要传入一个size就可以构建优先队列的结构（元素之间使用compareTo方法进行比较）。

public class PriorityQueue<T extends Comparable<? super T>> { 
    public PriorityQueue(int capacity) {
        currentSize = 0;
        array = (T[]) new Comparable[capacity + 1];
    }
}

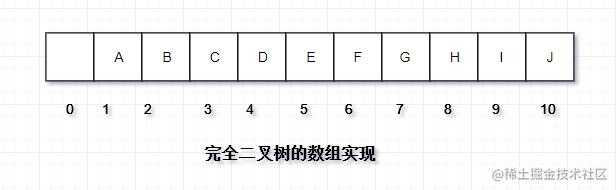
对于数组中的任意位置 i 的元素，其左儿子在位置 2i 上，则右儿子在 2i+1 上，父节点在 在 i/2（向下取整）上。通常从数组下标1开始存储，这样的好处在于很方便找到左右、及父节点。如果从0开始，左儿子在2i+1,右儿子在2i+2,父节点在(i-1)/2（向下取整）。

堆序性：

我们这建立最小堆，即对于每一个元素X，X的父亲中的关键字小于（或等于）X中的关键字，根节点除外（它没有父节点）。

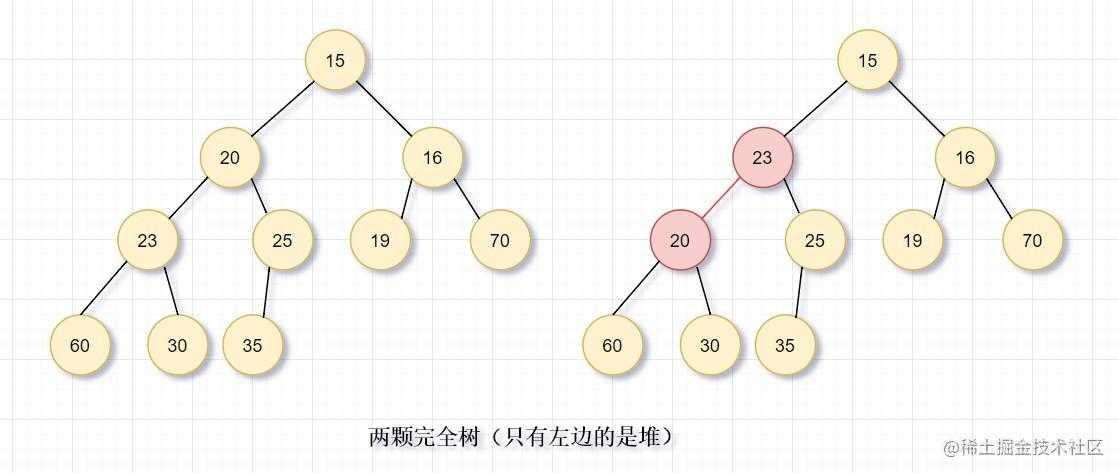
如图所示，只有左边是堆，右边红色节点违反堆序性。根据堆序性，只需要常O(1)找到最小元。

三、基本的堆操作

1. insert（插入）

• 上滤：为了插入元素X，我们在下一个可用的位置建立空穴（否则会破坏结构性，不是完全二叉树）。如果此元素放入空穴不破坏堆序性，则插入完成；否则，将父节点下移到空穴，即空穴向根的方向上冒一步。继续该过程，直到X插入空穴为止。这样的过程称为上滤。

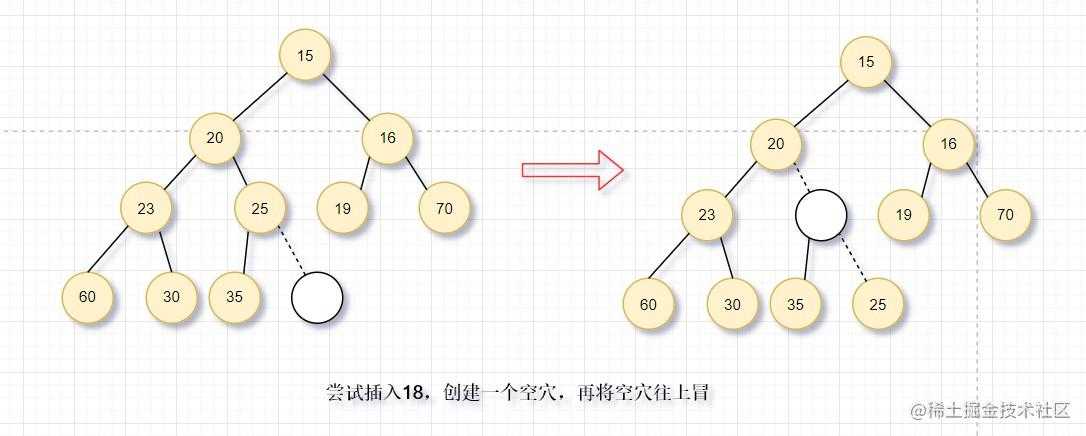
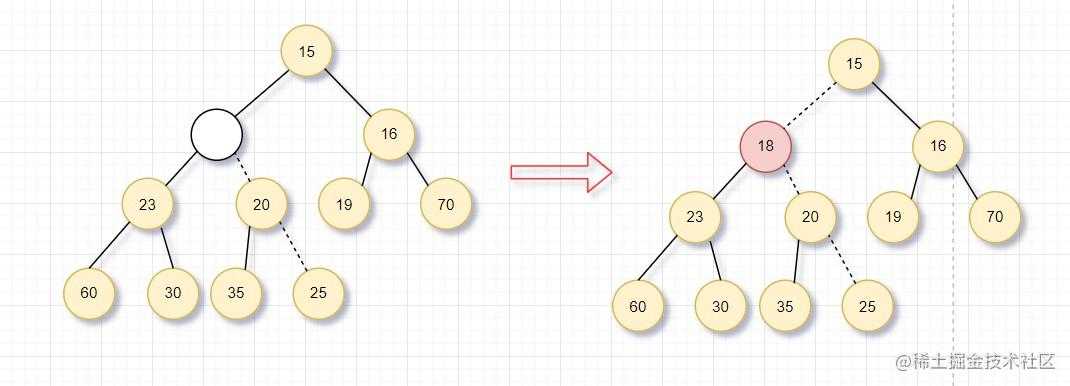
图中演示了18插入的过程，在下一个可用的位置建立空穴（满足结构性），发现不能直接插入，将父节点移下来，空穴上冒。继续这个过程，直到满足堆序性。这样就实现了元素插入到优先队列（堆）中。

• java实现上滤

     /**
     * 插入到优先队列，维护堆序性
     *
     * @param x ：插入的元素
     */
    public void insert(T x) {
        if (null == x) {
            return;
        }
        //扩容
        if (currentSize == array.length - 1) {
            enlargeArray(array.length * 2 + 1);
        }
        //上滤
        int hole = ++currentSize;
        for (array[0] = x; x.compareTo(array[hole / 2]) < 0; hole /= 2) {
            array[hole] = array[hole / 2];
        }
        array[hole] = x;
    }

    /**
     * 扩容方法
     *
     * @param newSize ：扩容后的容量，为原来的2倍+1
     */
    private void enlargeArray(int newSize) {
        T[] old = array;
        array = (T[]) new Comparable[newSize];
        System.arraycopy(old, 0, array, 0, old.length);
    }

可以反复使用交换操作来进行上滤过程，但如果插入X上滤d层，则需要3d次赋值；我们这种方式只需要d+1次赋值。

如果插入的元素是新的最小元从而一直上滤到根处，那么这种插入的时间长达O(logN)。但平均来看，上滤终止得要早。业已证明，执行依次插入平均需要2.607次比较，因此平均insert操作上移元素1.607层。上滤次数只比插入次数少一次。

2. deleteMin（删除最小元）

• 下滤：类似于上滤操作。因为我们建立的是最小堆，所以删除最小元，就是将根节点删掉，这样就破坏了结构性。所以我们在根节点处建立空穴，为了满足结构性，堆中最后一个元素X必须移动到合适的位置，如果可以直接放到空穴，则删除完成（一般不可能）；否则，将空穴的左右儿子中较小者移到空穴，即空穴下移了一层。继续这样的操作，直到X可以放入到空穴中。这样就可以满足结构性与堆序性。这个过程称为下滤。

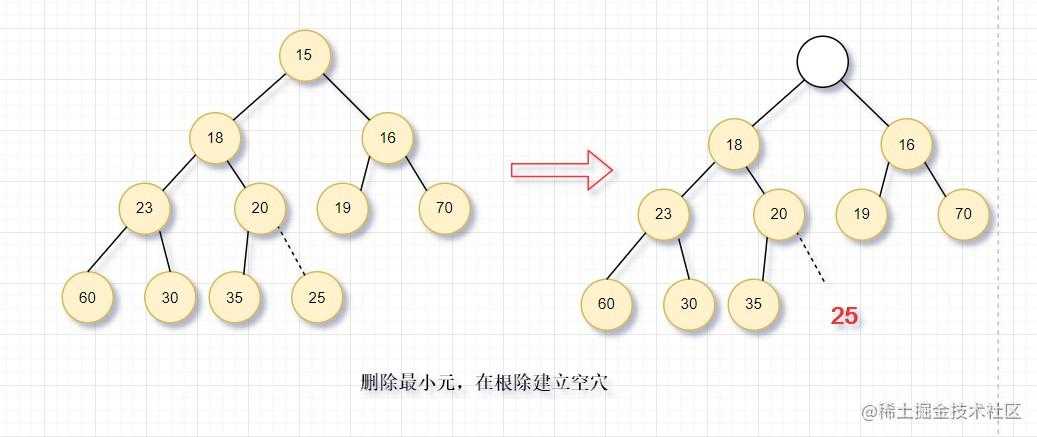
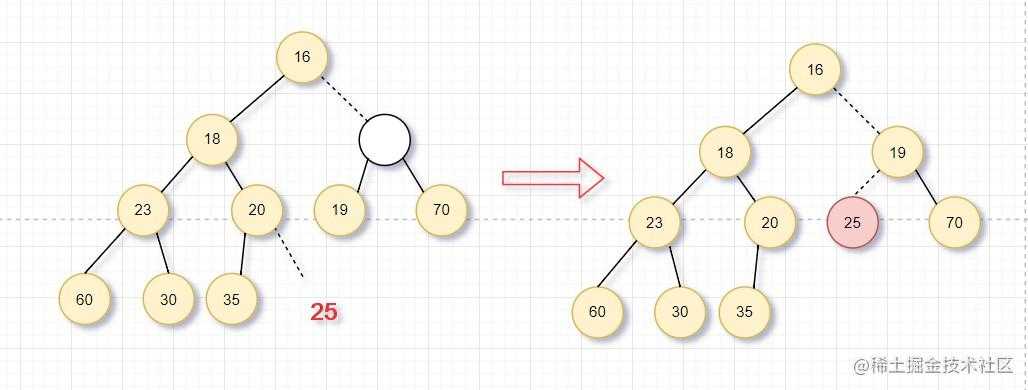
如图所示：在根处建立空穴，将最后一个元素放到空穴，已满足结构性；为满足堆序性，需要将空穴下移到合适的位置。

注意：堆的实现中，经常发生的错误是只有偶数个元素，即有一个节点只有一个儿子。所以需要测试右儿子的存在性。

/**
     * 删除最小元
     * 若优先队列为空，抛出UnderflowException
     *
     * @return ：返回最小元
     */
    public T deleteMin() {
        if (isEmpty()) {
            throw new UnderflowException();
        }

        T minItem = findMin();
        array[1] = array[currentSize--];
        percolateDown(1);

        return minItem;
    }

     /**
     * 下滤方法
     *
     * @param hole ：从数组下标hole1开始下滤
     */
    private void percolateDown(int hole) {
        int child;
        T tmp = array[hole];

        for (; hole * 2 <= currentSize; hole = child) {
            //左儿子
            child = hole * 2;
            //判断右儿子是否存在
            if (child != currentSize &&
                    array[child + 1].compareTo(array[child]) < 0) {
                child++;
            }
            if (array[child].compareTo(tmp) < 0) {
                array[hole] = array[child];
            } else {
                break;
            }
        }
        array[hole] = tmp;
    }

这种操作最坏时间复杂度是O(logN)。平均而言，被放到根处的元素几乎下滤到底层（即来自的那层），所以平均时间复杂度是O(logN)。

四、总结

优先队列常使用二叉堆实现，本篇图解了二叉堆最基本的两个操作：插入及删除最小元。insert以O(1)常数时间执行，deleteMin以O(logN)执行。相信大家看了之后就可以去看java的PriorityQueue源码了。今天只说了二叉堆最基本的操作，还有一些额外操作及分析下次再说。比如，如何证明buildHeap是线性的？以及优先队列的应用等。

声明：图文皆原创，如有转载，请注明出处。如有错误，请帮忙指出，欢迎讨论；若觉得可以，微微一赞支持支持。