前言
作为一个多年的老菜鸟,有感于大部分的公司面试 “面试造航母,工作螺丝钉” 的作风,特整理了这个数据结构和算法面试题系列。对于校招而言,如果没有太多实践/实习经验,大公司往往喜欢考察数据结构和算法,如微软就特别喜欢在校招时手写算法题,而且难度还不小,当年我毕业找工作时也是颇受折磨。
从第一篇文章到现在完成已然一个多月了,经 @掘金-yuzu柚子茶 的殷勤的催稿,终于在今天基本完成了。近一个月的业余时间全在这上面了,除了要将博文整合,还要将代码重新录入和测试,耗费不少精力。本系列的主要资料来源包括:《算法导论》、《编程珠玑》、《数据结构与算法-C语言实现》,面试题则多来自 leetcode、geeksforgeeks、编程之美等。
整理的博文系列名为 数据结构和算法面试题系列 ,是我6年前找工作时对数据结构和算法总结,其中有基础部分,也有各大公司的经典的面试题,最早发布在 CSDN 。由于之前的博文比较杂乱,且没有将实现代码统一整理,看起来会有诸多不便。现整理为一个系列给需要的朋友参考。本系列完整代码在 github 建了个仓库,所有代码都重新整理和做了一些基本的测试,代码仓库地址在这里: shishujuan/dsalg: 数据结构与算法系列汇总,如有错误,请在文章下面评论指出或者在 github 给我留言,我好及时改正以免误导其他朋友。
文章末尾有系列目录,可以按需取阅,如果需要测试,亦可以将仓库代码 clone 下来进行各种测试。如有错误或者引用不全、有侵权的地方,请大家给我指出,我好及时调整改正。系列文章总字数多达4万字,因此也整合了上下两篇文章给各位有需要的小伙伴,如果本系列有帮助到你,也欢迎点赞或者在 github 上 star✨✨,十分感谢。
数据结构和算法面试题系列—C指针、数组和结构体
0.概述
在用C语言实现一些常见的数据结构和算法时,C语言的基础不能少,特别是指针和结构体等知识。
1.关于 ELF 文件
linux 中的 C 编译得到的目标文件和可执行文件都是 ELF 格式的,可执行文件中以 segment 来划分,目标文件中,我们是以 section 划分。一个 segment 包含一个或多个 section,通过 readelf 命令可以看到完整的 section 和 segment 信息。看一个栗子🌰:
char pear[40];
static double peach;
int mango = 13;
char *str = "hello";
static long melon = 2001;
int main()
{
int i = 3, j;
pear[5] = i;
peach = 2.0 * mango;
return 0;
}
这是个简单的 C 语言代码,现在分析下各个变量存储的位置。其中 mango,melon 属于 data section,pear 和 peach 属于 common section 中,而且 peach 和 melon 加了 static,说明只能本文件使用。而 str 对应的字符串 “helloworld” 存储在 rodata section 中。
main 函数归属于 text section,函数中的局部变量 i,j 在运行时在栈中分配空间。注意到前面说的全局未初始化变量 peach 和 pear 是在 common section 中,这是为了强弱符号而设置的。那其实最终链接成为可执行文件后,会归于 BSS segment。同样的,text section 和 rodata section 在可执行文件中都属于同一个 segment。
更多 ELF 内容参见《程序猿的自我修养》一书。
2.指针
想当年学习 C 语言最怕的就是指针了,当然《c与指针》和《c专家编程》以及《高质量C编程》里面对指针都有很好的讲解,系统回顾还是看书吧,这里我总结了一些基础和易错的点。环境是 ubuntu14.10 的 32 位系统,编译工具 GCC。
2.1 指针易错点
/*** 指针易错示例1 demo1.c ***/
int main()
{
char *str = "helloworld"; //[1]
str[1] = 'M'; //[2] 会报错
char arr[] = "hello"; //[3]
arr[1] = 'M';
return 0;
}
demo1.c 中,我们定义了一个指针和数组分别指向了一个字符串,然后修改字符串中某个字符的值。编译后运行会发现[2]处会报错,这是为什么呢?用命令gcc -S demo1.c 生成汇编代码就会发现[1]处的 helloworld 是存储在 rodata section 的,是只读的,而[3]处的是存储在栈中的。所以[2]报错而[3]正常。在 C 中,用[1]中的方式创建字符串常量并赋值给指针,则字符串常量存储在 rodata section。而如果是赋值给数组,则存储在栈中或者 data section 中(如[3]就是存储在栈中)。示例 2 给出了更多容易出错的点,可以看看。
/*** 指针易错示例2 demo2.c ***/
char *GetMemory(int num) {
char *p = (char *)malloc(sizeof(char) * num);
return p;
}
char *GetMemory2(char *p) {
p = (char *)malloc(sizeof(char) * 100);
}
char *GetString(){
char *string = "helloworld";
return string;
}
char *GetString2(){
char string[] = "helloworld";
return string;
}
void ParamArray(char a[])
{
printf("sizeof(a)=%d\n", sizeof(a)); // sizeof(a)=4,参数以指针方式传递
}
int main()
{
int a[] = {1, 2, 3, 4};
int *b = a + 1;
printf("delta=%d\n", b-a); // delta=4,注意int数组步长为4
printf("sizeof(a)=%d, sizeof(b)=%d\n", sizeof(a), sizeof(b)); //sizeof(a)=16, sizeof(b)=4
ParamArray(a);
//引用了不属于程序地址空间的地址,导致段错误
/* int *p = 0; *p = 17; */
char *str = NULL;
str = GetMemory(100);
strcpy(str, "hello");
free(str); //释放内存
str = NULL; //避免野指针
//错误版本,这是因为函数参数传递的是副本。
/* char *str2 = NULL; GetMemory2(str2); strcpy(str2, "hello"); */
char *str3 = GetString();
printf("%s\n", str3);
//错误版本,返回了栈指针,编译器会有警告。
/* char *str4 = GetString2(); */
return 0;
}
2.2 指针和数组
在2.1中也提到了部分指针和数组内容,在C中指针和数组在某些情况下可以相互转换来使用,比如char *str="helloworld"可以通过str[1]来访问第二个字符,也可以通过*(str+1)来访问。 此外,在函数参数中,使用数组和指针也是等同的。但是指针和数组在有些地方并不等同,需要特别注意。
比如我定义一个数组char a[9] = "abcdefgh";(注意字符串后面自动补\0),那么用 a[1]读取字符 ‘b’ 的流程是这样的:
- 首先,数组a有个地址,我们假设是 9980。
- 然后取偏移值,偏移值为索引值*元素大小,这里索引是 1,char 大小也为1,因此加上 9980 为 9981,得到数组 a 第 1 个元素的地址。(如果是int类型数组,那么这里偏移就是1 * 4 = 4)
- 取地址 9981 处的值,就是’b’。
那如果定义一个指针char *a = "abcdefgh";,我们通过 a[1]来取第一个元素的值。跟数组流程不同的是:
- 首先,指针 a 自己有个地址,假设是 4541.
- 然后,从 4541 取 a 的值,也就是字符串 “abcdefgh” 的地址,假定是 5081。
- 接着就是跟之前一样的步骤了,5081 加上偏移 1 ,取 5082 地址处的值,这里就是’b’了。
通过上面的说明可以发现,指针比数组多了一个步骤,虽然看起来结果是一致的。因此,下面这个错误就比较好理解了。在 demo3.c 中定义了一个数组,然后在 demo4.c 中通过指针来声明并引用它,显然是会报错的。如果改成extern char p[];就正确了(当然声明你也可以写成 extern char p[3],声明里面的数组大小跟实际大小不一致是没有关系的),一定要保证定义和声明匹配。
/*** demo3.c ***/
char p[] = "helloworld";
/*** demo4.c ***/
extern char *p;
int main() {
printf("%c\n", p[1]);
return 0;
}
3.typedef 和 #define
typedef 和 #define 都是经常用的,但是它们是不一样的。一个 typedef 可以塞入多个声明器,而 #define 一般只能有一个定义。在连续声明中,typedef 定义的类型可以保证声明的变量都是同一种类型,而 #define 不行。此外,typedef 是一种彻底的封装类型,在声明之后不能再添加其他的类型。如代码中所示。
#define int_ptr int *
int_ptr i, j; //i是int *类型,而j是int类型。
typedef char * char_ptr;
char_ptr c1, c2; //c1, c2都是char *类型。
#define peach int
unsigned peach i; //正确
typdef int banana;
unsigned banana j; //错误,typedef声明的类型不能扩展其他类型。
另外,typedef 在结构体定义中也很常见,比如下面代码中的定义。需要注意的是,[1]和[2]是很不同的。当你如[1]中那样用 typedef 定义了 struct foo,那么其实除了本身的 foo 结构标签,你还定义了 foo 这种结构类型,所以可以直接用 foo 来声明变量。而如[2]中的定义是不能用 bar 来声明变量的,因为它只是一个结构变量,并不是结构类型。
还有一点需要说明的是,结构体是有自己名字空间的,所以结构体中的字段可以跟结构体名字相同,比如[3]中那样也是合法的,当然尽量不要这样用。后面一节还会更详细探讨结构体,因为在 Python 源码中也有用到很多结构体。
typedef struct foo {int i;} foo; //[1]
struct bar {int i;} bar; //[2]
struct foo f; //正确,使用结构标签foo
foo f; //正确,使用结构类型foo
struct bar b; //正确,使用结构标签bar
bar b; // 错误,使用了结构变量bar,bar已经是个结构体变量了,可以直接初始化,比如bar.i = 4;
struct foobar {int foorbar;}; //[3]合法的定义
4.结构体
在学习数据结构的时候,定义链表和树结构会经常用到结构体。比如下面这个:
struct node {
int data;
struct node* next;
};
在定义链表的时候可能就有点奇怪了,为什么可以这样定义,貌似这个时候 struct node 还没有定义好为什么就可以用 next 指针指向用这个结构体定义了呢?
4.1 不完全类型
这里要说下 C 语言里面的不完全类型。C 语言可以分为函数类型,对象类型以及不完全类型。而对象类型还可以分为标量类型和非标量类型。算术类型(如 int,float,char 等)和指针类型属于标量类型,而定义完整的结构体,联合体,数组等都是非标量类型。而不完全类型是指没有定义完整的类型,比如下面这样的:
struct s;
union u;
char str[];
具有不完全类型的变量可以通过多次声明组合成一个完全类型。比如下面 2 词声明 str 数组是合法的:
char str[];
char str[10];
此外,如果两个源文件定义了同一个变量,只要它们不全部是强类型的,那么也是可以编译通过的。比如下面这样是合法的,但是如果将 file1.c 中的int i;改成强定义如int i = 5;那么就会出错了。
//file1.c
int i;
//file2.c
int i = 4;
4.2 不完全类型结构体
不完全类型的结构体十分重要,比如我们最开始提到的 struct node 的定义,编译器从前往后处理,发现struct node *next时,认为 struct node 是一个不完全类型,next 是一个指向不完全类型的指针,尽管如此,指针本身是完全类型,因为不管什么指针在 32 位系统都是占用 4 个字节。而到后面定义结束,struct node 成了一个完全类型,从而 next 就是一个指向完全类型的指针了。
4.3 结构体初始化和大小
结构体初始化比较简单,需要注意的是结构体中包含有指针的时候,如果要进行字符串拷贝之类的操作,对指针需要额外分配内存空间。如下面定义了一个结构体 student 的变量 stu 和指向结构体的指针 pstu,虽然 stu 定义的时候已经隐式分配了结构体内存,但是你要拷贝字符串到它指向的内存的话,需要显示分配内存。
struct student {
char *name;
int age;
} stu, *pstu;
int main() {
stu.age = 13; //正确
// strcpy(stu.name,"hello"); //错误,name还没有分配内存空间
stu.name = (char *)malloc(6);
strcpy(stu.name, "hello"); //正确
return 0;
}
结构体大小涉及一个对齐的问题,对齐规则为:
- 结构体变量首地址为最宽成员长度(如果有
#pragma pack(n),则取最宽成员长度和n的较小值,默认pragma的n=8)的整数倍 - 结构体大小为最宽成员长度的整数倍
- 结构体每个成员相对结构体首地址的偏移量都是每个成员本身大小(如果有pragma pack(n),则是n与成员大小的较小值)的整数倍 因此,下面结构体S1和S2虽然内容一样,但是字段顺序不同,大小也不同,
sizeof(S1) = 8, 而sizeof(S2) = 12. 如果定义了#pragma pack(2),则sizeof(S1)=8;sizeof(S2)=8
typedef struct node1
{
int a;
char b;
short c;
}S1;
typedef struct node2
{
char b;
int a;
short c;
}S2;
4.4 柔性数组
柔性数组是指结构体的最后面一个成员可以是一个大小未知的数组,这样可以在结构体中存放变长的字符串。如代码中所示。**注意,柔性数组必须是结构体最后一个成员,柔性数组不占用结构体大小.**当然,你也可以将数组写成char str[0],含义相同。
注:在学习 Python 源码过程中,发现其柔性数组声明并不是用一个空数组或者 char str[0],而是用的char str[1],即数组大小为 1。这是因为 ISO C标准不允许声明大小为 0 的数组( gcc -pedanti 参数可以检查是否符合 ISO C 标准),为了可移植性,所以常常看到的是声明数组大小为1。当然,很多编译器比如 GCC 等把数组大小为 0 作为了一个非标准的扩展,所以声明空的或者大小为 0 的柔性数组在 GCC 中是可以正常编译的。
struct flexarray {
int len;
char str[];
} *pfarr;
int main()
{
char s1[] = "hello, world";
pfarr = malloc(sizeof(struct flexarray) + strlen(s1) + 1);
pfarr->len = strlen(s1);
strcpy(pfarr->str, s1);
printf("%d\n", sizeof(struct flexarray)); // 4
printf("%d\n", pfarr->len); // 12
printf("%s\n", pfarr->str); // hello, world
return 0;
}
5.总结
- 关于 const,c 语言中的 const 不是常量,所以不能用 const 变量来定义数组,如
const int N = 3; int a[N];这是错误的。 - 注意内存分配和释放,杜绝野指针。
- C 语言中弱符号和强符号一起链接是合法的。
- 注意指针和数组的区别。
- typedef 和 #define 是不同的。
- 注意包含指针的结构体的初始化和柔性数组的使用。
数据结构和算法面试题系列—字符串
0.概述
字符串作为数据结构中的基础内容,也是面试中经常会考察的基本功之一,比如实现 strcpy,strcmp 等基本函数等,回文字符串,字符串搜索,正则表达式等。本文相关代码见 这里。
1.基本操作
首先来看一些字符串的基本函数的实现,以下代码取自 MIT6.828 课程。
// 字符串长度
int strlen(const char *s) {
int n;
for (n = 0; *s != '\0'; s++)
n++;
return n;
}
// 字符串复制
char *strcpy(char *dst, const char *src) {
char *ret;
ret = dst;
while ((*dst++ = *src++) != '\0')
/* do nothing */;
return ret;
}
// 字符串拼接
char *strcat(char *dst, const char *src) {
int len = strlen(dst);
strcpy(dst + len, src);
return dst;
}
// 字符串比较
int strcmp(const char *p, const char *q) {
while (*p && *p == *q)
p++, q++;
return (int) ((unsigned char) *p - (unsigned char) *q);
}
// 返回字符串s中第一次出现c的位置
char *strchr(const char *s, char c) {
for (; *s; s++)
if (*s == c)
return (char *) s;
return 0;
}
// 设置内存位置v开始的n个元素值为c
void *memset(void *v, int c, size_t n) {
char *p;
int m;
p = v;
m = n;
while (--m >= 0)
*p++ = c;
return v;
}
// 内存拷贝,注意覆盖情况
void *memmove(void *dst, const void *src, size_t n) {
const char *s;
char *d;
s = src;
d = dst;
if (s < d && s + n > d) {
s += n;
d += n;
while (n-- > 0)
*--d = *--s;
} else
while (n-- > 0)
*d++ = *s++;
return dst;
}
2.字符串相关面试题
2.1 最长回文子串
题: 给定一个字符串,找出该字符串的最长回文子串。回文字符串指的就是从左右两边看都一样的字符串,如 aba,cddc 都是回文字符串。字符串 abbacdc 存在的回文子串有 abba 和 cdc,因此它的最长回文子串为 abba。
一个容易犯的错误
初看这个问题可能想到这样的方法:对字符串 S 逆序得到新的字符串 S’,再求 S 和 S’ 的最长公共子串,这样求出的就是最长回文子串。
- 如
S = caba,S' = abac,则 S 和 S’ 的最长公共子串为aba,这个是正确的。 - 但是如果
S = abacdfgdcaba,S’ = abacdgfdcaba,则 S 和 S’ 的最长公共子串为abacd,显然这不是回文字符串。因此这种方法是错误的。
判定一个字符串是否是回文字符串
要找出最长回文子串,首先要解决判断一个字符串是否是回文字符串的问题。最显而易见的方法是设定两个变量 i 和 j,分别指向字符串首部和尾部,比较是否相等,然后 i++,j--,直到 i >= j 为止。下面的代码是判断字符串 str[i, j] 是不是回文字符串,即字符串 str 从 i 到 j 的这一段子串是否是回文字符串,在后面会用到这个方法。
/** * 判断字符串s[start:end]是否是回文字符串 */
int isPalindrome(string s, int start, int end)
{
for (; start < end; ++start,--end) {
if (s[start] != s[end])
return 0;
}
return 1;
}
解1:蛮力法求最长子串
蛮力法通过对字符串所有子串进行判断,如果是回文字符串,则更新最长回文的长度。因为长度为 N 的字符串的子串一共可能有 (1+N)*N/2 个,每次判断子串需要 O(N) 的时间,所以一共需要 O(N^3) 时间求最长回文子串。
/**
* 最长回文子串-蛮力法 O(N^3)
*/
string longestPalindrome(string s)
{
int len = s.length(), maxLen = 1;
int start=0, i, j;
/*遍历字符串所有的子串,若子串为回文字符串则更新最长回文的长度*/
for (i = 0; i < len - 1; i++) {
for (j = i + 1; j < len; j++) {
if (isPalindrome(s, i, j)) { //如果str[i,j]是回文,则判断其长度是否大于最大值,大于则更新长度和位置
int pLen = j - i + 1;
if (pLen > maxLen) {
start = i; //更新最长回文起始位置
maxLen = pLen; //更新最长回文的长度
}
}
}
}
return s.substr(start, maxLen);
}
解2:动态规划法
因为蛮力法判定回文的时候需要很多重复的计算,所以可以通过动态规划法来改进该算法。假定我们知道“bab”是回文,则“ababa”也一定是回文。
定义P[i, j] = true 如果子串P[i, j]是回文字符串。
则 P[i, j] <- (P[i+1, j-1] && s[i] = s[j])。
Base Case:
P[i, i ] = true
P[i, i+1 ] = true <- s[i] = s[i+1]
据此,实现代码如下:
/**
* 最长回文子串-动态规划法,该方法的时间复杂度为O(N^2),空间复杂度为O(N^2)。
*/
/**
* 最长回文子串-动态规划法,该方法的时间复杂度为O(N^2),空间复杂度为O(N^2)。
*
* 思想:定义P[i, j] = 1 如果子串P[i, j]是回文字符串。
* 则 P[i, j] <- (P[i+1, j-1] && s[i] == s[j])。
*
* Base Case:
* P[ i, i ] <- 1
* P[ i, i+1 ] <- s[i] == s[i+1]
*/
string longestPalindromeDP(string s)
{
int n = s.length();
int longestBegin = 0, maxLen = 1;
int **P;
int i;
/*构造二维数组P*/
P = (int **)calloc(n, sizeof(int *));
for (i = 0; i < n; i++) {
P[i] = (int *)calloc(n, sizeof(int));
}
for (i = 0; i < n; i++) {
P[i][i] = 1;
}
for (int i=0; i<n-1; i++) {
if (s[i] == s[i+1]) {
P[i][i+1] = 1;
longestBegin = i;
maxLen = 2;
}
}
/*依次求P[i][i+2]...P[i][i+n-1]等*/
int len = 3;
for (; len <= n; ++len) {
for (i = 0; i < n-len+1; ++i) {
int j = i + len - 1;
if (s[i] == s[j] && P[i+1][j-1]) {
P[i][j] = 1;
longestBegin = i;
maxLen = len;
}
}
}
/*释放内存*/
for (i = 0; i< n; i++)
free(P[i]);
free(P);
return s.substr(longestBegin, maxLen);
}
解3:中心法
还有一个更简单的方法可以使用 O(N^2) 时间、不需要额外的空间求最长回文子串。我们知道回文字符串是以字符串中心对称的,如 abba 以及 aba 等。一个更好的办法是从中间开始判断,因为回文字符串以字符串中心对称。一个长度为 N 的字符串可能的对称中心有 2N-1 个,至于这里为什么是 2N-1 而不是 N 个,是因为可能对称的点可能是两个字符之间,比如 abba 的对称点就是第一个字母 b 和第二个字母 b 的中间。据此实现代码如下:
/**
* 求位置l为中心的最长回文子串的开始位置和长度
*/
void expandAroundCenter(string s, int l, int r, int *longestBegin, int *longestLen)
{
int n = s.length();
while (l>=0 && r<=n-1 && s[l]==s[r]) {
l--, r++;
}
*longestBegin = l + 1;
*longestLen = r - l - 1;
}
/**
* 最长回文子串-中心法,时间O(N^2)。
*/
string longestPalindromeCenter(string s)
{
int n = s.length();
if (n == 0)
return s;
char longestBegin = 0;
int longestLen = 1;
for (int i = 0; i < n; i++) {
int iLongestBegin, iLongestLen;
expandAroundCenter(s, i, i, &iLongestBegin, &iLongestLen); //以位置i为中心的最长回文字符串
if (iLongestLen > longestLen) {
longestLen = iLongestLen;
longestBegin = iLongestBegin;
}
expandAroundCenter(s, i, i+1, &iLongestBegin, &iLongestLen); //以i和i+1之间的位置为中心的最长回文字符串
if (iLongestLen > longestLen) {
longestLen = iLongestLen;
longestBegin = iLongestBegin;
}
}
return s.substr(longestBegin, longestLen);
}
2.2 交换排序
题: 已知一个字符数组,其中存储有 R、G、B 字符,要求将所有的字符按照 RGB 的顺序进行排序。比如给定一个数组为 char s[] = "RGBBRGGBGB",则排序后应该为 RRGGGGBBBB。
解1: 这个题目有点类似于快速排序中用到的划分数组的方法,但是这里有三个字符,因此需要调用划分方法两次,第一次以 B 划分,第二次以 G 划分,这样两次划分后就可以将原来的字符数组划分成 RGB 顺序。这个方法比较自然,容易想到,代码如下。这个方法的缺点是需要遍历两遍数组。
void swapChar(char *s, int i, int j)
{
char temp = s[i];
s[i] = s[j];
s[j] = temp;
}
/** * 划分函数 */
void partition(char *s, int lo, int hi, char t)
{
int m = lo-1, i;
for (i = lo; i <= hi; i++) {
if (s[i] != t) {
swapChar(s, ++m ,i);
}
}
}
/** * RGB排序-遍历两次 */
void rgbSortTwice(char *s)
{
int len = strlen(s);
partition(s, 0, len-1, 'G'); // 以G划分,划分完为 RBBRBBGGGG
partition(s, 0, len-1, 'B'); // 再以B划分,划分完为 RRGGGGBBBB
}
解2: 其实还有一个只需要遍历一遍数组的方法,当然该方法虽然只遍历一遍数组,但是需要交换的次数并未减少。主要是设置两个变量 r 和 g 分别指示当前 R 和 G 字符所在的位置,遍历数组。
-
1)如果第 i 个位置为字符 R,则与前面的指示变量 r 的后一个字符也就是 ++r 处的字符交换,并 ++g,此时还需要判断交换后的 i 里面存储的字符是否是 G,如果是 G,则需要将其与 g 处的字符交换;
-
2)如果第 i 个位置为字符 G,则将其与 ++g 处的字符交换即可。++g 指向的总是下一个应该交换 G 的位置,++r 指向的是下一个需要交换 R 的位置。
-
3)如果第 i 个位置为字符B,则什么都不做,继续遍历。
/**
* RGB排序-遍历一次
*/
void rgbSortOnce(char *s)
{
int len = strlen(s);
int lo = 0, hi = len - 1;
int r, g, i; //++r和++g分别指向R和G交换的位置
r = g = lo - 1;
for (i = lo; i <= hi; i++) {
if (s[i] == 'R') { // 遇到R
swapChar(s, ++r, i);
++g;
if (s[i] == 'G') // 交换后的值是G,继续交换
swapChar(s, g, i);
} else if (s[i] == 'G') { // 遇到G
swapChar(s, ++g, i);
} else { // 遇到B,什么都不做
}
}
}
解3: 如果不考虑用交换的思想,可以直接统计 RGB 各个字符的个数,然后从头开始对数组重新赋值为 RGB 即可。那样简单多了,哈哈。但是如果换一个题,要求是对正数、负数、0 按照一定顺序排列,那就必须用交换了。
2.3 最大滑动窗口
题: 给定一个数组 A,有一个大小为 w 的滑动窗口,该滑动窗口从最左边滑到最后边。在该窗口中你只能看到 w 个数字,每次只能移动一个位置。我们的目的是找到每个窗口 w 个数字中的最大值,并将这些最大值存储在数组 B 中。
例如数组 A = [1 3 -1 -3 5 3 6 7], 窗口大小 w = 3 。则窗口滑动过程如下所示:
Window position Max
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
输入: 数组A和w大小
输出: 数组B,其中B[i]存储了A[i]到A[i+w-1]中w个数字的最大值。
解1:简单实现
一个最简单的想法就是每次移动都计算 w 个数字的最大值并保存起来,每次计算 w 个数字的最大值需要 O(w) 的时间,而滑动过程需要滑动 n-w+1 次,n 为数组大小,因此总共的时间为 O(nw) 。
/* * 求数组最大值 */
int maxInArray(int A[], int n)
{
int max = A[0], i;
for (i = 1; i < n; i++) {
if (A[i] > max) {
max = A[i];
}
}
return max;
}
/* * 最大滑动窗口-简单实现 */
void maxSlidingWindowSimple(int A[], int n, int w, int B[])
{
int i;
for (i = 0; i <= n-w; i++)
B[i] = maxInArray(A + i, w);
}
解2:最大堆解法
第1个方法思路简单,但是时间复杂度过高,因此需要改进。可以使用一个最大堆来保存 w 个数字,每次插入数字时只需要 O(lgw) 的时间,从堆中取最大值只需要 O(1) 的时间(堆的平均大小约为 w )。随着窗口由左向右滑动,因此堆中有些数字会失效(因为它们不再包含在窗口中)。如果数组本身有序,则堆大小会增大到 n。因为堆大小并不保持在 w 不变,因此该算法时间复杂度为 O(nlgn)。
/** * 最大滑动窗口-最大堆解法 */
void maxSlidingWindowPQ(int A[], int n, int w, int B[])
{
typedef pair<int, int> Pair;
priority_queue<Pair> Q; //优先级队列保存窗口里面的值
for (int i = 0; i < w; i++)
Q.push(Pair(A[i], i)); //构建w个元素的最大堆
for (int i = w; i < n; i++) {
Pair p = Q.top();
B[i-w] = p.first;
while (p.second <= i-w) {
Q.pop();
p = Q.top();
}
Q.push(Pair(A[i], i));
}
B[n-w] = Q.top().first;
}
解3:双向队列解法
最大堆解法在堆中保存有冗余的元素,比如原来堆中元素为 [10 5 3],新的元素为 11,则此时堆中会保存有 [11 5 3]。其实此时我们可以清空整个队列,然后再将 11 加入到队列即可,即只在队列中保持 [11]。使用双向队列可以满足要求,滑动窗口的最大值总是保存在队列首部,队列里面的数据总是从大到小排列。当遇到比当前滑动窗口最大值更大的值时,则将队列清空,并将新的最大值插入到队列中。如果遇到的值比当前最大值小,则直接插入到队列尾部。每次移动的时候需要判断当前的最大值是否在有效范围,如果不在,则需要将其从队列中删除。由于每个元素最多进队和出队各一次,因此该算法时间复杂度为O(N)。
/** * 最大滑动窗口-双向队列解法 */
void maxSlidingWindowDQ(int A[], int n, int w, int B[])
{
deque<int> Q;
for (int i = 0; i < w; i++) {
while (!Q.empty() && A[i] >= A[Q.back()])
Q.pop_back();
Q.push_back(i);
}
for (int i = w; i < n; i++) {
B[i-w] = A[Q.front()];
while (!Q.empty() && A[i] >= A[Q.back()])
Q.pop_back();
while (!Q.empty() && Q.front() <= i-w)
Q.pop_front();
Q.push_back(i);
}
B[n-w] = A[Q.front()];
}
2.4 最长公共子序列
题: 给定两个序列 X = < x1, x2, …, xm > 和 Y = < y1, y2, …, ym >,希望找出X和Y最大长度的公共子序列(LCS)。
分析: 解决LCS的最简单的是使用蛮力法,穷举 X 的所有子序列,然后逐一检查是否是 Y 的子序列,并记录发现的最长子序列,最终取最大的子序列即可。但是 X 所有子序列有 2^m,该方法需要指数级时间,不太切实际,然而LCS问题其实具有最优子结构性质。
LCS最优子结构:
如 X = <A, B, C, B, D, A, B>, Y = <B, D, C, A, B, A>,则 X 和 Y 的最长公共子序列为 <B, C, B, A> 或者 <B, D, A, B>。也就是说,LCS可能存在多个。
设 X = < x1, x2, …, xm > 和 Y = < y1, y2, …, yn > 为两个序列,并设 Z = < z1, z2, …, zk > 为 X 和 Y 的任意一个LCS。
-
- 如果 xm = yn,那么 zk = xm = yn,且 Zk-1 是 Xm-1 和 Yn-1 的一个LCS。
-
- 如果 xm != yn,那么 zk != xm,且 Z 是 Xm-1 和 Y 的一个LCS。
-
- 如果 xm != yn,那么 zk != yn,且 Z 是 X 和 Yn-1 的一个LCS。
因此,我们可以定义 c[i, j] 为序列 Xi 和 Yj 的一个LCS的长度,则可以得到下面的递归式:
c[i, j] = 0 // i = 0 或者 j = 0
c[i, j] = c[i-1, j-1] + 1 // i,j > 0,且 Xi = Yj
c[i, j] = max(c[i-1, j], c[i][j-1]) // i, j > 0,且 Xi != Yj
据此可以写出如下代码求 LCS 的长度及 LCS,使用一个辅助数组 b 存储 LCS 路径。这里给出递归算法求 LCS 长度,使用动态规划算法的代码见本文源码。
/**
* LCS-递归算法
*/
#define UP 1
#define LEFT 2
#define UPLEFT 3
int lcsLengthRecur(char *X, int m, char *Y, int n, int **b)
{
if (m == 0 || n == 0)
return 0;
if (X[m-1] == Y[n-1]) {
b[m][n] = UPLEFT;
return lcsLengthRecur(X, m-1, Y, n-1, b) + 1;
}
int len1 = lcsLengthRecur(X, m-1, Y, n, b);
int len2 = lcsLengthRecur(X, m, Y, n-1, b);
int maxLen;
if (len1 >= len2) {
maxLen = len1;
b[m][n] = UP;
} else {
maxLen = len2;
b[m][n] = LEFT;
}
return maxLen;
}
/**
* 打印LCS,用到辅助数组b
*/
void printLCS(int **b, char *X, int i, int j)
{
if (i == 0 || j == 0)
return;
if (b[i][j] == UPLEFT) {
printLCS(b, X, i-1, j-1);
printf("%c ", X[i-1]);
} else if (b[i][j] == UP) {
printLCS(b, X, i-1, j);
} else {
printLCS(b, X, i, j-1);
}
}
打印LCS的流程如下图所示(图取自算法导论):

2.5 字符串全排列
题: 给一个字符数组 char arr[] = "abc",输出该数组中字符的全排列。
解: 使用递归来输出全排列。首先明确的是 perm(arr, k, len) 函数的功能:输出字符数组 arr 从位置 k 开始的所有排列,数组长度为 len 。基础条件是 k == len-1,此时已经到达最后一个元素,一次排列已经完成,直接输出。否则,从位置k开始的每个元素都与位置k的值交换(包括自己与自己交换),然后进行下一次排列,排列完成后记得恢复原来的序列。
假定数组 arr 大小 len=3,则程序调用 perm(arr, 0, 3) 可以如下理解: 第一次交换 0,0,并执行 perm(arr, 1, 3),执行完再次交换0,0,数组此时又恢复成初始值。 第二次交换 1,0(注意数组此时是初始值),并执行 perm(arr, 1, 3), 执行完再次交换 1,0,数组此时又恢复成初始值。 第三次交换 2,0,并执行 perm(arr, 1, 3),执行完成后交换2,0,数组恢复成初始值。
程序运行输出结果为:abc acb bac bca cba cab。即先输出以 a 为排列第一个值的排列,而后是 b 和 c 为第一个值的排列。
void perm(char *arr, int k, int len) { //k为起始位置,len为数组大小
if (k == len-1) {
printf("%s\n", arr);
return;
}
for (int i = k; i < len; i++) {
swapChar(arr, i, k); //交换
perm(arr, k+1, len); //下一次排列
swapChar(arr, i, k); //恢复原来的序列
}
}
2.6 正则表达式
题: 实现一个简易版的正则表达式,支持 ^、$、.等特性。
正则表达式基础:一个正则表达式本身也是一个字符序列,它定义了能与之匹配的字符串集合。在 Unix/Linux 通用的正则表达式中,字符 ^ 表示字符串开始, $ 表示字符串结束。这样,^x 只能与位于字符串开始处的 x匹配, x$ 只能匹配结尾的 x,^x$只能匹配单个字符的串里的 x,而^$只能匹配空串。字符 . 能与任意字符匹配。所以,模式 x.y能匹配 xay、x2y 等等,但它不能匹配 xy 或 xaby。显然 ^.$ 能够与任何单个字符的串匹配。写在方括号 [] 里的一组字符能与这组字符中的任一个相匹配。如 [0123456789] 能与任何数字匹配。这个模式也可以简写为 [0-9]。
解: 下面是正则表达式匹配的主函数 match,接收参数为匹配模式 regexp 和文本 text。 如果正则表达式的开头是 ^,那么正文必须从起始处与表达式的其余部分匹配。否则,我们就沿着串走下去,用 matchhere() 看正文是否能在某个位置上匹配。一旦发现了匹配,工作就完成了。注意这里 do-while的使用,有些表达式能与空字符串匹配 (例如: $ 能够在字符串的末尾与空字符串匹配,* 能匹配任意个数的字符,包括 0 个)。所以,即使遇到了空字符串,我们也还需要调用 matchhere()。
int match(const char *regexp, const char *text) {
if (regexp[0] == '^')
return matchhere(regexp+1, text);
do {
if (matchhere(regexp, text))
return 1;
} while (*text++ != '\0');
return 0;
}
递归函数 matchhere() 完成大部分的匹配工作:
- 如果
regexp[0]=='\0',表示已经匹配到末尾,则匹配成功,返回1。 - 如果表达式的最后是
$,匹配成功的条件是正文也到达了末尾,即判断*text=='\0'。如果正文text也到了末尾,则匹配成功,否则失败。 - 如果正文没有到末尾,且
regexp[0] == *text或者regexp=='.'(.表示匹配任意字符),则递归调用matchhere继续下一次匹配。 - 如果
regexp[1]=='*',则过程稍显复杂,例如x*。这时我们调用matchstar来处理,其第一个参数是星号的参数 (x*中的x),随后的参数是位于星号之后的模式,以及对应的正文串。
int matchhere(const char *regexp, const char *text) {
if (regexp[0] == '\0')
return 1;
if (regexp[0]=='$' && regexp[1]=='\0')
return *text == '\0';
if (regexp[1] == '*')
return matchstar(regexp[0], regexp+2, text);
if (*text != '\0' && (regexp[0] == '.' || regexp[0] == *text))
return matchhere(regexp+1, text+1);
return 0;
}
int matchstar(int c, const char *regexp, const char *text) {
do {
if (matchhere(regexp, text))
return 1;
} while (*text != '\0' && (*text++ == c || c == '.'));
return 0;
}
示例:
char *regexp="abc", text="dagabcdefg",匹配成功。char *regexp="^abc", *text="abcdefg",匹配成功。char *regexp="^abc", *text="bcdefgabc",匹配失败。char *regexp="abc$", *text="defghabc",匹配成功。
2.7 KMP算法和BM算法
字符串匹配的大名鼎鼎的有KMP算法和BM算法,网上资料比较多,可以参见 grep之字符串搜索算法Boyer-Moore由浅入深(比KMP快3-5倍) 和 字符串匹配的KMP算法 。
数据结构和算法面试题系列—链表
0.概述
链表作为一种基础的数据结构,在很多地方会用到。如在 Linux 内核代码,redis 源码,python 源码中都有使用。除了单向链表,还有双向链表,本文主要关注单向链表(含部分循环链表题目,会在题目中注明,其他情况都是讨论简单的单向链表)。双向链表在redis中有很好的实现,也在我的仓库中拷贝了一份用于测试用,本文的相关代码在 这里。
1.定义
先定义一个单向链表结构,如下,定义了链表结点和链表两个结构体。这里我没有多定义一个链表的结构体,保存头指针,尾指针,链表长度等信息,目的也是为了多练习下指针的操作。
// aslist.h
// 链表结点定义
typedef struct ListNode {
struct ListNode *next;
int value;
} listNode;

2.基本操作
在上一节的链表定义基础上,我们完成几个基本操作函数,包括链表初始化,链表中添加结点,链表中删除结点等。
/**
* 创建链表结点
*/
ListNode *listNewNode(int value)
{
ListNode *node;
if (!(node = malloc(sizeof(ListNode))))
return NULL;
node->value = value;
node->next = NULL;
return node;
}
/**
* 头插法插入结点。
*/
ListNode *listAddNodeHead(ListNode *head, int value)
{
ListNode *node;
if (!(node = listNewNode(value)))
return NULL;
if (head)
node->next = head;
head = node;
return head;
}
/**
* 尾插法插入值为value的结点。
*/
ListNode *listAddNodeTail(ListNode *head, int value)
{
ListNode *node;
if (!(node = listNewNode(value)))
return NULL;
return listAddNodeTailWithNode(head, node);
}
/**
* 尾插法插入结点。
*/
ListNode *listAddNodeTailWithNode(ListNode *head, ListNode *node)
{
if (!head) {
head = node;
} else {
ListNode *current = head;
while (current->next) {
current = current->next;
}
current->next = node;
}
return head;
}
/**
* 从链表删除值为value的结点。
*/
ListNode *listDelNode(ListNode *head, int value)
{
ListNode *current=head, *prev=NULL;
while (current) {
if (current->value == value) {
if (current == head)
head = head->next;
if (prev)
prev->next = current->next;
free(current);
break;
}
prev = current;
current = current->next;
}
return head;
}
/**
* 链表遍历。
*/
void listTraverse(ListNode *head)
{
ListNode *current = head;
while (current) {
printf("%d", current->value);
printf("->");
current = current->next;
if (current == head) // 处理首尾循环链表情况
break;
}
printf("NULL\n");
}
/**
* 使用数组初始化一个链表,共len个元素。
*/
ListNode *listCreate(int a[], int len)
{
ListNode *head = NULL;
int i;
for (i = 0; i < len; i++) {
if (!(head = listAddNodeTail(head, a[i])))
return NULL;
}
return head;
}
/**
* 链表长度函数
*/
int listLength(ListNode *head)
{
int len = 0;
while (head) {
len++;
head = head->next;
}
return len;
}
3.链表相关面试题
3.1 链表逆序
题: 给定一个单向链表 1->2->3->NULL,逆序后变成 3->2->1->NULL。
解: 常见的是用的循环方式对各个结点逆序连接,如下:
/**
* 链表逆序,非递归实现。
*/
ListNode *listReverse(ListNode *head)
{
ListNode *newHead = NULL, *current = head;
while (current) {
ListNode *next = current->next;
current->next = newHead;
newHead = current;
current = next;
}
return newHead;
}
如果带点炫技性质的,那就来个递归的解法,如下:
/**
* 链表逆序,递归实现。
*/
ListNode *listReverseRecursive(ListNode *head)
{
if (!head || !head->next) {
return head;
}
ListNode *reversedHead = listReverseRecursive(head->next);
head->next->next = head;
head->next = NULL;
return reversedHead;
}
3.2 链表复制
题: 给定一个单向链表,复制并返回新的链表头结点。
解: 同样可以有两种解法,非递归和递归的,如下:
/**
* 链表复制-非递归
*/
ListNode *listCopy(ListNode *head)
{
ListNode *current = head, *newHead = NULL, *newTail = NULL;
while (current) {
ListNode *node = listNewNode(current->value);
if (!newHead) { // 第一个结点
newHead = newTail = node;
} else {
newTail->next = node;
newTail = node;
}
current = current->next;
}
return newHead;
}
/**
* 链表复制-递归
*/
ListNode *listCopyRecursive(ListNode *head)
{
if (!head)
return NULL;
ListNode *newHead = listNewNode(head->value);
newHead->next = listCopyRecursive(head->next);
return newHead;
}
3.3 链表合并
题: 已知两个有序单向链表,请合并这两个链表,使得合并后的链表仍然有序(注:这两个链表没有公共结点,即不交叉)。如链表1是 1->3->4->NULL,链表2是 2->5->6->7->8->NULL,则合并后的链表为 1->2->3->4->5->6->7->8->NULL。
解: 这个很类似归并排序的最后一步,将两个有序链表合并到一起即可。使用2个指针分别遍历两个链表,将较小值结点归并到结果链表中。如果一个链表归并结束后另一个链表还有结点,则把另一个链表剩下部分加入到结果链表的尾部。代码如下所示:
/**
* 链表合并-非递归
*/
ListNode *listMerge(ListNode *list1, ListNode *list2)
{
ListNode dummy; // 使用空结点保存合并链表
ListNode *tail = &dummy;
if (!list1)
return list2;
if (!list2)
return list1;
while (list1 && list2) {
if (list1->value <= list2->value) {
tail->next = list1;
tail = list1;
list1 = list1->next;
} else {
tail->next = list2;
tail = list2;
list2 = list2->next;
}
}
if (list1) {
tail->next = list1;
} else if (list2) {
tail->next = list2;
}
return dummy.next;
}
当然,要实现一个递归的也不难,代码如下:
ListNode *listMergeRecursive(ListNode *list1, ListNode *list2)
{
ListNode *result = NULL;
if (!list1)
return list2;
if (!list2)
return list1;
if (list1->value <= list2->value) {
result = list1;
result->next = listMergeRecursive(list1->next, list2);
} else {
result = list2;
result->next = listMergeRecursive(list1, list2->next);
}
return result;
}
3.4 链表相交判断
题: 已知两个单向链表list1,list2,判断两个链表是否相交。如果相交,请找出相交的结点。
解1: 可以直接遍历list1,然后依次判断list1每个结点是否在list2中,但是这个解法的复杂度为 O(length(list1) * length(list2))。当然我们可以遍历list1时,使用哈希表存储list1的结点,这样再遍历list2即可判断了,时间复杂度为O(length(list1) + length(list2)),空间复杂度为 O(length(list1)),这样相交的结点自然也就找出来了。当然,找相交结点还有更好的方法。
解2: 两个链表如果相交,那么它们从相交后的节点一定都是相同的。假定list1长度为len1,list2长度为len2,且 len1 > len2,则我们只需要将 list1 先遍历 len1-len2个结点,然后两个结点一起遍历,如果遇到相等结点,则该结点就是第一个相交结点。
/**
* 链表相交判断,如果相交返回相交的结点,否则返回NULL。
*/
ListNode *listIntersect(ListNode *list1, ListNode *list2)
{
int len1 = listLength(list1);
int len2 = listLength(list2);
int delta = abs(len1 - len2);
ListNode *longList = list1, *shortList = list2;
if (len1 < len2) {
longList = list2;
shortList = list1;
}
int i;
for (i = 0; i < delta; i++) {
longList = longList->next;
}
while (longList && shortList) {
if (longList == shortList)
return longList;
longList = longList->next;
shortList = shortList->next;
}
return NULL;
}
3.5 判断链表是否存在环
题: 给定一个链表,判断链表中是否存在环。

解1: 容易想到的方法就是使用一个哈希表记录出现过的结点,遍历链表,如果一个结点重复出现,则表示该链表存在环。如果不用哈希表,也可以在链表结点 ListNode 结构体中加入一个 visited 字段做标记,访问过标记为 1,也一样可以检测。由于目前我们还没有实现一个哈希表,这个方法代码后面再加。
解2: 更好的一种方法是 Floyd判圈算法,该算法最早由罗伯特.弗洛伊德发明。通过使用两个指针 fast 和 slow 遍历链表,fast 指针每次走两步,slow 指针每次走一步,如果 fast 和 slow 相遇,则表示存在环,否则不存在环。(注意,如果链表只有一个节点且没有环,不会进入 while 循环)
/**
* 检测链表是否有环-Flod判圈算法
* 若存在环,返回相遇结点,否则返回NULL
*/
ListNode *listDetectLoop(ListNode *head)
{
ListNode *slow, *fast;
slow = fast = head;
while (slow && fast && fast->next) {
slow = slow->next;
fast = fast->next->next;
if (slow == fast) {
printf("Found Loop\n");
return slow;
}
}
printf("No Loop\n");
return NULL;
}
void testListDetectLoop()
{
printf("\nTestListDetectLoop\n");
int a[] = {1, 2, 3, 4};
ListNode *head = listCreate(a, ALEN(a));
listDetectLoop(head);
// 构造一个环
head->next->next->next = head;
listDetectLoop(head);
}
扩展: 检测到有环的话,那要如何找链表的环的入口点呢?
首先,我们来证明一下为什么上面的解 2 提到的算法是正确的。如果链表不存在环,因为快指针每次走 2 步,必然会比慢指针先到达链表尾部,不会相遇。
如果存在环,假定快慢指针经过s次循环后相遇,则此时快指针走的距离为 2s,慢指针走的距离为 s,假定环内结点数为 r,则要相遇则必须满足下面条件,即相遇时次数满足 s = nr。即从起点之后下一次相遇需要循环 r 次。
2s - s = nr => s = nr
如下图所示,环长度 r=4,则从起点后下一次相遇需要经过 4 次循环。
那么环的入口点怎么找呢?前面已经可知道第一次相遇要循环 r 次,而相遇时慢指针走的距离为 s = r,设链表总长度为 L,链表头到环入口的距离为 a,环入口到相遇点的距离为 x,则 L = a + r,可以推导出 a = (L-x-a),其中 L-x-a 为相遇点到环入口点的距离,即链表头到环入口的距离a等于相遇点到环入口距离。
s = r = a + x => a + x = (L-a) => a = L-x-a
于是,在判断链表存在环后,从相遇点和头结点分别开始遍历,两个指针每次都走一步,当两个指针相等时,就是环的入口点。
/**
* 查找链表中环入口
*/
ListNode *findLoopNode(ListNode *head)
{
ListNode *meetNode = listDetectLoop(head);
if (!meetNode)
return NULL;
ListNode *headNode = head;
while (meetNode != headNode) {
meetNode = meetNode->next;
headNode = headNode->next;
}
return meetNode;
}
3.6 链表模拟加法
题: 给定两个链表,每个链表的结点值为数字的各位上的数字,试求出两个链表所表示数字的和,并将结果以链表形式返回。假定两个链表分别为 list1 和 list2,list1 各个结点值分别为数字 513 的个位、十位和百位上的数字,同理 list2 的各个结点值为数字 295 的各位上的数字。则这两个数相加为 808,所以输出按照从个位到百位顺序输出,返回的结果链表如下。
list1: (3 -> 1 -> 5 -> NULL)
list2: (5 -> 9 -> 2 -> NULL)
result: (8 -> 0 -> 8 -> NULL)
解: 这个题目比较有意思,需要对链表操作比较熟练。我们考虑两个数字相加过程,从低位到高位依次相加,如果有进位则标记进位标志,直到最高位才终止。设当前位的结点为 current,则有:
current -> data = list1 -> data + list2 -> data + carry
(其中 carry 为低位的进位,如果有进位为 1,否则为 0)
非递归代码如下:
/**
* 链表模拟加法-非递归解法
*/
ListNode *listEnumarateAdd(ListNode *list1, ListNode *list2)
{
int carry = 0;
ListNode *result = NULL;
while (list1 || list2 || carry) {
int value = carry;
if (list1) {
value += list1->value;
list1 = list1->next;
}
if (list2) {
value += list2->value;
list2 = list2->next;
}
result = listAddNodeTail(result, value % 10);
carry = ( value >= 10 ? 1: 0);
}
return result;
}
非递归实现如下:
/**
* 链表模拟加法-递归解法
*/
ListNode *listEnumarateAddRecursive(ListNode *list1, ListNode *list2, int carry)
{
if (!list1 && !list2 && carry==0)
return NULL;
int value = carry;
if (list1)
value += list1->value;
if (list2)
value += list2->value;
ListNode *next1 = list1 ? list1->next : NULL;
ListNode *next2 = list2 ? list2->next : NULL;
ListNode *more = listEnumarateAddRecursive(next1, next2, (value >= 10 ? 1 : 0));
ListNode *result = listNewNode(carry);
result->value = value % 10;
result->next = more;
return result;
}
3.7 有序单向循环链表插入结点
题: 已知一个有序的单向循环链表,插入一个结点,仍保持链表有序,如下图所示。
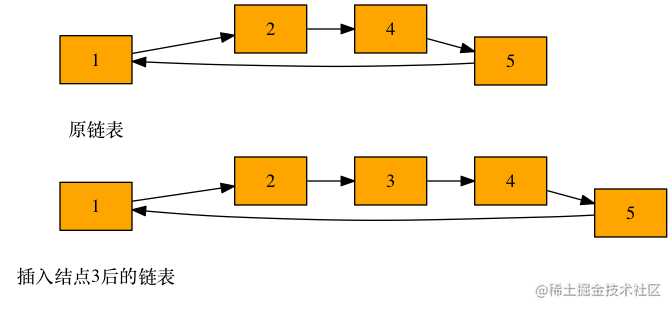
解: 在解决这个问题前,我们先看一个简化版本,就是在一个有序无循环的单向链表中插入结点,仍然保证其有序。这个问题的代码相信多数人都很熟悉,一般都是分两种情况考虑:
- 1)如果原来链表为空或者插入的结点值最小,则直接插入该结点并设置为头结点。
- 2)如果原来链表非空,则找到第一个大于该结点值的结点,并插入到该结点的前面。如果插入的结点值最大,则插入在尾部。
实现代码如下:
/**
* 简化版-有序无循环链表插入结点
*/
ListNode *sortedListAddNode(ListNode *head, int value)
{
ListNode *node = listNewNode(value);
if (!head || head->value >= value) { //情况1
node->next = head;
head = node;
} else { //情况2
ListNode *current = head;
while (current->next != NULL && current->next->value < value)
current = current->next;
node->next = current->next;
current->next = node;
}
return head;
}
当然这两种情况也可以一起处理,使用二级指针。如下:
/**
* 简化版-有序无循环链表插入结点(两种情况一起处理)
*/
void sortedListAddNodeUnify(ListNode **head, int value)
{
ListNode *node = listNewNode(value);
ListNode **current = head;
while ((*current) && (*current)->value < value) {
current = &((*current)->next);
}
node->next = *current;
*current = node;
}
接下来看循环链表的情况,其实也就是需要考虑下面2点:
- 1) prev->value ≤ value ≤ current->value: 插入到prev和current之间。
- 2) value为最大值或者最小值: 插入到首尾交接处,如果是最小值重新设置head值。
代码如下:
/**
* 有序循环链表插入结点
*/
ListNode *sortedLoopListAddNode(ListNode *head, int value)
{
ListNode *node = listNewNode(value);
ListNode *current = head, *prev = NULL;
do {
prev = current;
current = current->next;
if (value >= prev->value && value <= current->value)
break;
} while (current != head);
prev->next = node;
node->next = current;
if (current == head && value < current->value) // 判断是否要设置链表头
head = node;
return head;
}
3.8 输出链表倒数第K个结点
题: 给定一个简单的单向链表,输出链表的倒数第K个结点。
解1: 如果是顺数第 K 个结点,不用多思考,直接遍历即可。这个题目的新意在于它是要输出倒数第 K 个结点。一个直观的想法是,假定链表长度为 L,则倒数第 K 个结点就是顺数的 L-K+1 个结点。如链表长度为 3,倒数第 2 个,就是顺数的第 2 个结点。这样需要遍历链表 2 次,一次求长度,一次找结点。
/**
* 链表倒数第K个结点-遍历两次算法
*/
ListNode *getLastKthNodeTwice(ListNode *head, int k)
{
int len = listLength(head);
if (k > len)
return NULL;
ListNode *current = head;
int i;
for (i = 0; i < len-k; i++) //遍历链表,找出第N-K+1个结点
current = current->next;
return current;
}
解2: 当然更好的一种方法是遍历一次,设置两个指针p1,p2,首先 p1 和 p2 都指向 head,然后 p2 向前走 k 步,这样 p1 和 p2 之间就间隔 k 个节点。最后 p1 和 p2 同时向前移动,p2 走到链表末尾的时候 p1 刚好指向倒数第 K 个结点。代码如下:
/**
* 链表倒数第K个结点-遍历一次算法
*/
ListNode *getLastKthNodeOnce(ListNode *head, int k)
{
ListNode *p1, *p2;
p1 = p2 = head;
for(; k > 0; k--) {
if (!p2) // 链表长度不够K
return NULL;
p2 = p2->next;
}
while (p2) {
p1 = p1->next;
p2 = p2->next;
}
return p1;
}
数据结构和算法面试题系列—栈
这个系列是我多年前找工作时对数据结构和算法总结,其中有基础部分,也有各大公司的经典的面试题,最早发布在CSDN。现整理为一个系列给需要的朋友参考,如有错误,欢迎指正。本系列完整代码地址在 这里。
0.概述
栈作为一种基本的数据结构,在很多地方有运用,比如函数递归,前后缀表达式转换等。本文会用 C 数组来实现栈结构(使用链表实现可以参见链表那一节,使用头插法构建链表即可),并对常见的几个跟栈相关的面试题进行分析,本文代码在 这里。
1.定义
我们使用结构体来定义栈,使用柔性数组来存储元素。几个宏定义用于计算栈的元素数目及栈是否为空和满。
typedef struct Stack {
int capacity;
int top;
int items[];
} Stack;
#define SIZE(stack) (stack->top + 1)
#define IS_EMPTY(stack) (stack->top == -1)
#define IS_FULL(stack) (stack->top == stack->capacity - 1)
2.基本操作
栈主要有三种基本操作:
- push:压入一个元素到栈中。
- pop:弹出栈顶元素并返回。
- peek:取栈顶元素,但是不修改栈。
如图所示:

代码如下:
Stack *stackNew(int capacity)
{
Stack *stack = (Stack *)malloc(sizeof(*stack) + sizeof(int) * capacity);
if (!stack) {
printf("Stack new failed\n");
exit(E_NOMEM);
}
stack->capacity = capacity;
stack->top = -1;
return stack;
}
void push(Stack *stack, int v)
{
if (IS_FULL(stack)) {
printf("Stack Overflow\n");
exit(E_FULL);
}
stack->items[++stack->top] = v;
}
int pop(Stack *stack)
{
if (IS_EMPTY(stack)) {
printf("Stack Empty\n");
exit(E_EMPTY);
}
return stack->items[stack->top--];
}
int peek(Stack *stack)
{
if (IS_EMPTY(stack)) {
printf("Stack Empty\n");
exit(E_EMPTY);
}
return stack->items[stack->top];
}
3.栈相关面试题
3.1 后缀表达式求
题: 已知一个后缀表达式 6 5 2 3 + 8 * + 3 + *,求该后缀表达式的值。
解: 后缀表达式也叫逆波兰表达式,其求值过程可以用到栈来辅助存储。则其求值过程如下:
- 1)遍历表达式,遇到的数字首先放入栈中,此时栈为
[6 5 2 3]。 - 2)接着读到
+,则弹出3和2,计算3 + 2,计算结果等于5,并将5压入到栈中,栈为[6 5 5]。 - 3)读到
8,将其直接放入栈中,[6 5 5 8]。 - 4)读到
*,弹出8和5,计算8 * 5,并将结果40压入栈中,栈为[6 5 40]。而后过程类似,读到+,将40和5弹出,将40 + 5的结果45压入栈,栈变成[6 45],读到3,放入栈[6 45 3]…以此类推,最后结果为288。
代码:
int evaluatePostfix(char *exp)
{
Stack* stack = stackNew(strlen(exp));
int i;
if (!stack) {
printf("New stack failed\n");
exit(E_NOMEM);
}
for (i = 0; exp[i]; ++i) {
// 如果是数字,直接压栈
if (isdigit(exp[i])) {
push(stack, exp[i] - '0');
} else {// 如果遇到符号,则弹出栈顶两个元素计算,并将结果压栈
int val1 = pop(stack);
int val2 = pop(stack);
switch (exp[i])
{
case '+': push(stack, val2 + val1); break;
case '-': push(stack, val2 - val1); break;
case '*': push(stack, val2 * val1); break;
case '/': push(stack, val2/val1); break;
}
}
}
return pop(stack);
}
3.2 栈逆序
题: 给定一个栈,请将其逆序。
解1: 如果不考虑空间复杂度,完全可以另外弄个辅助栈,将原栈数据全部 pop 出来并 push 到辅助栈即可。
解2: 如果在面试中遇到这个题目,那肯定是希望你用更好的方式实现。可以先实现一个在栈底插入元素的函数,然后便可以递归实现栈逆序了,不需要用辅助栈。
* 在栈底插入一个元素
*/
void insertAtBottom(Stack *stack, int v)
{
if (IS_EMPTY(stack)) {
push(stack, v);
} else {
int x = pop(stack);
insertAtBottom(stack, v);
push(stack, x);
}
}
/** * 栈逆序 */
void stackReverse(Stack *stack)
{
if (IS_EMPTY(stack))
return;
int top = pop(stack);
stackReverse(stack);
insertAtBottom(stack, top);
}
3.3 设计包含 min 函数的栈
题: 设计一个栈,使得push、pop以及min(获取栈中最小元素)能够在常数时间内完成。
分析: 刚开始很容易想到一个方法,那就是额外建立一个最小二叉堆保存所有元素,这样每次获取最小元素只需要 O(1) 的时间。但是这样的话,为了建最小堆 push 和 pop 操作就需要 O(lgn) 的时间了(假定栈中元素个数为n),不符合题目的要求。
解1:辅助栈方法
那为了实现该功能,可以使用辅助栈使用一个辅助栈来保存最小元素,这个解法简单不失优雅。设该辅助栈名字为 minStack,其栈顶元素为当前栈中的最小元素。这意味着
- 1)要获取当前栈中最小元素,只需要返回 minStack 的栈顶元素即可。
- 2)每次执行 push 操作时,检查 push 的元素是否小于或等于 minStack 栈顶元素。如果是,则也push 该元素到 minStack 中。
- 3)当执行 pop 操作的时候,检查 pop 的元素是否与当前最小值相等。如果相等,则需要将该元素从minStack 中 pop 出去。
代码:
void minStackPush(Stack *orgStack, Stack *minStack, int v)
{
if (IS_FULL(orgStack)) {
printf("Stack Full\n");
exit(E_FULL);
}
push(orgStack, v);
if (IS_EMPTY(minStack) || v < peek(minStack)) {
push(minStack, v);
}
}
int minStackPop(Stack *orgStack, Stack *minStack)
{
if (IS_EMPTY(orgStack)) {
printf("Stack Empty\n");
exit(E_EMPTY);
}
if (peek(orgStack) == peek(minStack)) {
pop(minStack);
}
return pop(orgStack);
}
int minStackMin(Stack *minStack)
{
return peek(minStack);
}
示例:
另外一种解法利用存储差值而不需要辅助栈,方法比较巧妙:
- 栈顶多出一个空间用于存储栈最小值。
push时压入的是当前元素与压入该元素前的栈中最小元素(栈顶的元素)的差值,然后通过比较当前元素与当前栈中最小元素大小,并将它们中的较小值作为新的最小值压入栈顶。pop函数执行的时候,先pop出栈顶的两个值,这两个值分别是当前栈中最小值min和最后压入的元素与之前栈中最小值的差值delta。根据delta < 0或者delta >= 0来获得之前压入栈的元素的值和该元素出栈后的新的最小值。min函数则是取栈顶元素即可。
代码:
void minStackPushUseDelta(Stack *stack, int v)
{
if (IS_EMPTY(stack)) { // 空栈,直接压入v两次
push(stack, v);
push(stack, v);
} else {
int oldMin = pop(stack); // 栈顶保存的是压入v之前的栈中最小值
int delta = v - oldMin;
int newMin = delta < 0 ? v : oldMin;
push(stack, delta); // 压入 v 与之前栈中的最小值之差
push(stack, newMin); // 最后压入当前栈中最小值
}
int minStackPopUseDelta(Stack *stack)
{
int min = pop(stack);
int delta = pop(stack);
int v, oldMin;
if (delta < 0) { // 最后压入的元素比min小,则min就是最后压入的元素
v = min;
oldMin = v - delta;
} else { // 最后压入的值不是最小值,则min为oldMin。
oldMin = min;
v = oldMin + delta;
}
if (!IS_EMPTY(stack)) { // 如果栈不为空,则压入oldMin
push(stack, oldMin);
}
return v;
}
int minStackMinUseDelta(Stack *stack)
{
return peek(stack);
}
示例:
push(3): [3 3] push(4): [3 1 3] push(2): [3 1 -1 2] push(5): [3 1 -1 3 2] push(1): [3 1 -1 3 -1 1] min(): 1,pop(): 1,[3 1 -1 3 2] min(): 2,pop(): 5,[3 1 -1 2] min(): 2,pop(): 2,[3 1 3] min(): 3,pop(): 4,[3 3] min(): 3,pop(): 3,[ ] 3.4 求出栈数目和出栈序列
求出栈数目
题: 已知一个入栈序列,试求出所有可能的出栈序列数目。例如入栈序列为 1,2,3,则可能的出栈序列有5种:1 2 3,1 3 2 ,2 1 3,2 3 1,3 2 1。
解: 要求解出栈序列的数目,还算比较容易的。已经有很多文章分析过这个问题,最终答案就是卡特兰数,也就是说 n 个元素的出栈序列的总数目等于 C(2n, n) - C(2n, n-1) = C(2n, n) / (n+1) ,如 3 个元素的总的出栈数目就是 C(6, 3) / 4 = 5。
如果不分析求解的通项公式,是否可以写程序求出出栈的序列数目呢?答案是肯定的,我们根据当前栈状态可以将 出栈一个元素 和 入栈一个元素 两种情况的总的数目相加即可得到总的出栈数目。
/** * 计算出栈数目 * - in:目前栈中的元素数目 * - out:目前已经出栈的元素数目 * - wait:目前还未进栈的元素数目 */
int sumOfStackPopSequence(Stack *stack, int in, int out, int wait) {
if (out == stack->capacity) { // 元素全部出栈了,返回1
return 1;
}
int sum = 0;
if (wait > 0) // 进栈一个元素
sum += sumOfStackPopSequence(stack, in + 1, out, wait - 1);
if (in > 0) // 出栈一个元素
sum += sumOfStackPopSequence(stack, in - 1, out + 1, wait);
return sum;
}
求所有出栈序列
题: 给定一个输入序列 input[] = {1, 2, 3},打印所有可能的出栈序列。
解: 这个有点难,不只是出栈数目,需要打印所有出栈序列,需要用到回溯法,回溯法比简单的递归要难不少,后面有时间再单独整理一篇回溯法的文章。出栈序列跟入栈出栈的顺序有关,对于每个输入,都会面对两种情况: 是先将原栈中元素出栈还是先入栈 ,这里用到两个栈来实现,其中栈 stk 用于模拟入栈出栈,而栈 output 用于存储出栈的值。注意退出条件是当遍历完所有输入的元素,此时栈 stk 和 output 中都可能有元素,需要先将栈 output 从栈底开始打印完,然后将栈 stk 从栈顶开始打印即可。 另外一点就是,当我们使用的模拟栈 stk 为空时,则这个分支结束。代码如下:
void printStackPopSequence(int input[], int i, int n, Stack *stk, Stack *output)
{
if (i >= n) {
stackTraverseBottom(output); // output 从栈底开始打印
stackTraverseTop(stk); // stk 从栈顶开始打印
printf("\n");
return;
}
push(stk, input[i]);
printStackPopSequence(input, i+1, n, stk, output);
pop(stk);
if (IS_EMPTY(stk))
return;
int v = pop(stk);
push(output, v);
printStackPopSequence(input, i, n, stk, output);
push(stk, v);
pop(output);
}
数据结构和算法面试题系列—二叉堆
0.概述
本文要描述的堆是二叉堆。二叉堆是一种数组对象,可以被视为一棵完全二叉树,树中每个结点和数组中存放该结点值的那个元素对应。树的每一层都是填满的,最后一层除外。二叉堆可以用于实现堆排序,优先级队列等。本文代码地址在 这里。
1.二叉堆定义
使用数组来实现二叉堆,二叉堆两个属性,其中 LENGTH(A) 表示数组 A 的长度,而 HEAP_SIZE(A) 则表示存放在A中的堆的元素个数,其中 LENGTH(A) <= HEAP_SIZE(A),也就是说虽然 A[0,1,...N-1] 都可以包含有效值,但是 A[HEAP_SIZE(A)-1] 之后的元素不属于相应的堆。
二叉堆对应的树的根为 A[0],给定某个结点的下标 i ,可以很容易计算它的父亲结点和儿子结点。注意在后面的示例图中我们标注元素是从1开始计数的,而实现代码中是从0开始计数。
#define PARENT(i) ( i > 0 ? (i-1)/2 : 0)
#define LEFT(i) (2 * i + 1)
#define RIGHT(i) (2 * i + 2)
注:堆对应的树每一层都是满的,所以一个高度为 h 的堆中,元素数目最多为 1+2+2^2+...2^h = 2^(h+1) - 1(满二叉树),元素数目最少为 1+2+...+2^(h-1) + 1 = 2^h。 由于元素数目 2^h <= n <= 2^(h+1) -1,所以 h <= lgn < h+1,因此 h = lgn 。即一个包含n个元素的二叉堆高度为 lgn 。
2.保持堆的性质
本文主要建立一个最大堆,最小堆原理类似。为了保持堆的性质,maxHeapify(int A[], int i) 函数让堆数组 A 在最大堆中下降,使得以 i 为根的子树成为最大堆。
void maxHeapify(int A[], int i, int heapSize)
{
int l = LEFT(i);
int r = RIGHT(i);
int largest = i;
if (l <= heapSize-1 && A[l] > A[i]) {
largest = l;
}
if (r <= heapSize-1 && A[r] > A[largest]) {
largest = r;
}
if (largest != i) { // 最大值不是i,则需要交换i和largest的元素,并递归调用maxHeapify。
swapInt(A, i, largest);
maxHeapify(A, largest, heapSize);
}
}
-
在算法每一步里,从元素
A[i]和A[left]以及A[right]中选出最大的,将其下标存在largest中。如果A[i]最大,则以i为根的子树已经是最大堆,程序结束。 -
否则,
i的某个子结点有最大元素,将A[i]与A[largest]交换,从而使i及其子女满足最大堆性质。此外,下标为largest的结点在交换后值变为A[i],以该结点为根的子树又有可能违反最大堆的性质,所以要对该子树递归调用maxHeapify()函数。
当 maxHeapify() 函数作用在一棵以 i 为根结点的、大小为 n 的子树上时,运行时间为调整 A[i]、A[left]、A[right] 的时间 O(1),加上对以 i 为某个子结点为根的子树递归调用 maxHeapify 的时间。i 结点为根的子树大小最多为 2n/3(最底层刚好半满的时候),所以可以推得 T(N) <= T(2N/3) + O(1),所以 T(N)=O(lgN)。
下图是一个运行 maxHeapify(heap, 2) 的例子。A[] = {16, 4, 10, 14, 7, 9, 3, 2, 8, 1},堆大小为 10。
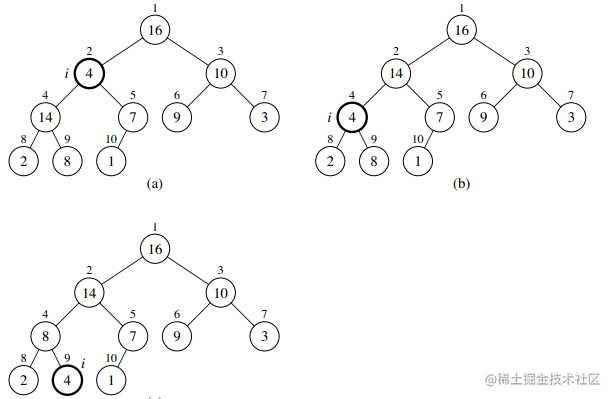
3.建立最大堆
我们可以知道,数组 A[0, 1, ..., N-1] 中,A[N/2, ..., N-1] 的元素都是树的叶结点。如上面图中的 6-10 的结点都是叶结点。每个叶子结点可以看作是只含一个元素的最大堆,因此我们只需要对其他的结点调用 maxHeapify() 函数即可。
void buildMaxHeap(int A[], int n)
{
int i;
for (i = n/2-1; i >= 0; i--) {
maxHeapify(A, i, n);
}
}
之所以这个函数是正确的,我们需要来证明一下,可以使用循环不变式来证明。
循环不变式:在for循环开始前,结点 i+1、i+2...N-1 都是一个最大堆的根。
初始化:for循环开始迭代前,i = N/2-1, 结点 N/2, N/2+1, ..., N-1都是叶结点,也都是最大堆的根。
保持:因为结点 i 的子结点标号都比 i 大,根据循环不变式的定义,这些子结点都是最大堆的根,所以调用 maxHeapify() 后,i 成为了最大堆的根,而 i+1, i+2, ..., N-1仍然保持最大堆的性质。
终止:过程终止时,i=0,因此结点 0, 1, 2, ..., N-1都是最大堆的根,特别的,结点0就是一个最大堆的根。
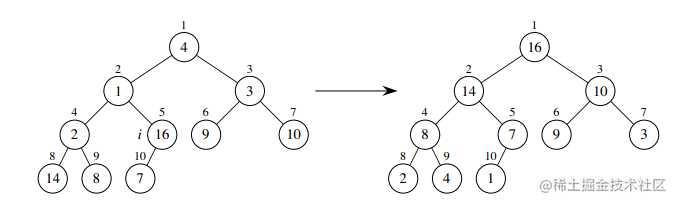
虽然每次调用 maxHeapify() 时间为 O(lgN),共有 O(N) 次调用,但是说运行时间是 O(NlgN) 是不确切的,准确的来说,运行时间为 O(N),这里就不证明了,具体证明过程参见《算法导论》。
4.堆排序
开始用 buildMaxHeap() 函数创建一个最大堆,因为数组最大元素在 A[0],通过直接将它与 A[N-1] 互换来达到最终正确位置。去掉 A[N-1],堆的大小 heapSize 减 1,调用 maxHeapify(heap, 0, --heapSize) 保持最大堆的性质,直到堆的大小由 N 减到 1。
void heapSort(int A[], int n)
{
buildMaxHeap(A, n);
int heapSize = n;
int i;
for (i = n-1; i >= 1; i--) {
swapInt(A, 0, i);
maxHeapify(A, 0, --heapSize);
}
}
5.优先级队列
最后实现一个最大优先级队列,主要有四种操作,分别如下所示:
insert(PQ, key):将 key 插入到队列中。maximum(PQ): 返回队列中最大关键字的元素extractMax(PQ):去掉并返回队列中最大关键字的元素increaseKey(PQ, i, key):将队列 i 处的关键字的值增加到 key
这里定义一个结构体 PriorityQueue 便于操作。
typedef struct PriorityQueue {
int capacity;
int size;
int elems[];
} PQ;
最终优先级队列的操作实现代码如下:
/**
* 从数组创建优先级队列
*/
PQ *newPQ(int A[], int n)
{
PQ *pq = (PQ *)malloc(sizeof(PQ) + sizeof(int) * n);
pq->size = 0;
pq->capacity = n;
int i;
for (i = 0; i < pq->capacity; i++) {
pq->elems[i] = A[i];
pq->size++;
}
buildMaxHeap(pq->elems, pq->size);
return pq;
}
int maximum(PQ *pq)
{
return pq->elems[0];
}
int extractMax(PQ *pq)
{
int max = pq->elems[0];
pq->elems[0] = pq->elems[--pq->size];
maxHeapify(pq->elems, 0, pq->size);
return max;
}
PQ *insert(PQ *pq, int key)
{
int newSize = ++pq->size;
if (newSize > pq->capacity) {
pq->capacity = newSize * 2;
pq = (PQ *)realloc(pq, sizeof(PQ) + sizeof(int) * pq->capacity);
}
pq->elems[newSize-1] = INT_MIN;
increaseKey(pq, newSize-1, key);
return pq;
}
void increaseKey(PQ *pq, int i, int key)
{
int *elems = pq->elems;
elems[i] = key;
while (i > 0 && elems[PARENT(i)] < elems[i]) {
swapInt(elems, PARENT(i), i);
i = PARENT(i);
}
}
数据结构和算法面试题系列—二叉树基础
0.概述
在说二叉树前,先来看看什么是树。树中基本单位是结点,结点之间的链接,称为分支。一棵树最上面的结点称之为根节点,而下面的结点为子结点。一个结点可以有 0 个或多个子结点,没有子结点的结点我们称之为叶结点。
二叉树是指子结点数目不超过 2 个的树,它是一种很经典的数据结构。而二叉搜索树(BST)是有序的二叉树,BST 需要满足如下条件:
- 若任意结点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意结点的右子树不空,则右子树上所有节点的值均大于或等于它的根节点的值;(有些书里面定义为 BST 不能有相同值结点,本文将相同值结点插入到右子树)
- 任意结点的左、右子树也分别为二叉查找树;
本文接下来会从定义,二叉搜索树的增删查以及二叉树的递归和非递归遍历进行整理。 下一篇文章会对二叉树相关的经典面试题进行全面解析,本文代码在 这里。
1.定义
我们先定义一个二叉树的结点,如下:
typedef struct BTNode {
int value;
struct BTNode *left;
struct BTNode *right;
} BTNode;
其中 value 存储值,left 和 right 指针分别指向左右子结点。二叉搜索树跟二叉树可以使用同一个结构,只是在插入或者查找时会有不同。
2.基本操作
接下来看看二叉树和二叉查找树的一些基本操作,包括 BST 插入结点,BST 查找结点,BST 最大值和最小值,二叉树结点数目和高度等。二叉查找树( BST )特有的操作都在函数前加了 bst 前缀区分,其他函数则是二叉树通用的。
1) 创建结点
分配内存,初始化值即可
/**
* 创建BTNode
*/
BTNode *newNode(int value)
{
BTNode *node = (BTNode *)malloc(sizeof(BTNode));
node->value = value;
node->left = node->right = NULL;
return node;
}
2) BST 插入结点
插入结点可以用递归或者非递归实现,如果待插入值比根节点值大,则插入到右子树中,否则插入到左子树中。如下图所示(图来自参考资料1,2,3):

/**
* BST中插入值,递归方法
*/
/**
* BST中插入结点,递归方法
*/
BTNode *bstInsert(BTNode *root, int value)
{
if (!root)
return newNode(value);
if (root->value > value) {
root->left = bstInsert(root->left, value);
} else {
root->right = bstInsert(root->right, value);
}
return root;
}
/**
* BST中插入结点,非递归方法
*/
BTNode *bstInsertIter(BTNode *root, int value)
{
BTNode *node = newNode(value);
if (!root)
return node;
BTNode *current = root, *parent = NULL;
while (current) {
parent = current;
if (current->value > value)
current = current->left;
else
current = current->right;
}
if (parent->value >= value)
parent->left = node;
else
parent->right = node;
return root;
}
3) BST 删除结点
删除结点稍微复杂一点,要考虑3种情况:
- 删除的是叶子结点,好办,移除该结点并将该叶子结点的父结点的
left或者right指针置空即可。
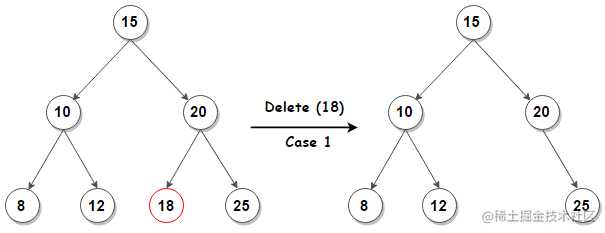
- 删除的结点有两个子结点,则需要找到该结点左子树的最大结点(使用后面的
bstSearchIter函数),并将其值替换到待删除结点中,然后递归调用删除函数删除该结点左子树最大结点即可。
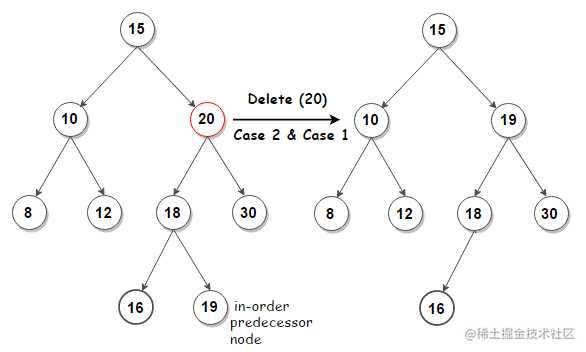
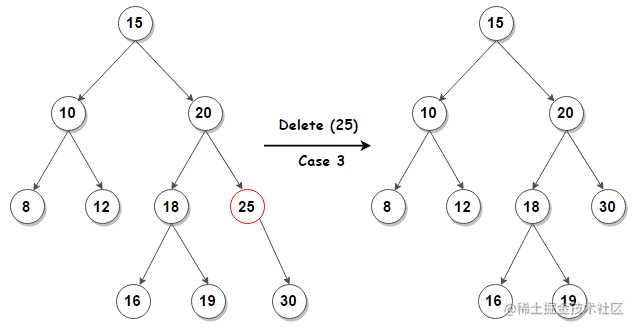
- 删除的结点只有一个子结点,则移除该结点并将其子结点的值填充到该删除结点即可(需要判断是左孩子还是右孩子结点)。
/**
* BST中删除结点
*/
BTNode *bstDelete(BTNode *root, int value)
{
BTNode *parent = NULL, *current = root;
BTNode *node = bstSearchIter(root, &parent, value);
if (!node) {
printf("Value not found\n");
return root;
}
if (!node->left && !node->right) {
// 情况1:待删除结点是叶子结点
if (node != root) {
if (parent->left == node) {
parent->left = NULL;
} else {
parent->right = NULL;
}
} else {
root = NULL;
}
free(node);
} else if (node->left && node->right) {
// 情况2:待删除结点有两个子结点
BTNode *predecessor = bstMax(node->left);
bstDelete(root, predecessor->value);
node->value = predecessor->value;
} else {
// 情况3:待删除结点只有一个子结点
BTNode *child = (node->left) ? node->left : node->right;
if (node != root) {
if (node == parent->left)
parent->left = child;
else
parent->right = child;
} else {
root = child;
}
free(node);
}
return root;
}
4) BST 查找结点
注意在非递归查找中会将父结点也记录下来。
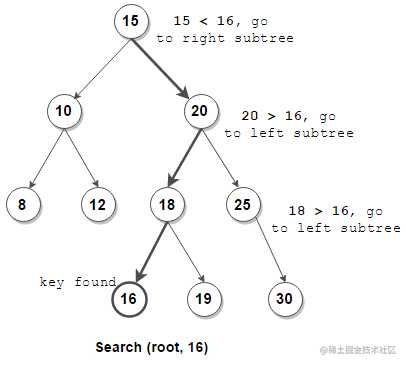
/** * BST查找结点-递归 */
BTNode *bstSearch(BTNode *root, int value)
{
if (!root) return NULL;
if (root->value == value) {
return root;
} else if (root->value > value) {
return bstSearch(root->left, value);
} else {
return bstSearch(root->left, value);
}
}
/** * BST查找结点-非递归 */
BTNode *bstSearchIter(BTNode *root, BTNode **parent, int value)
{
if (!root) return NULL;
BTNode *current = root;
while (current && current->value != value) {
*parent = current;
if (current->value > value)
current = current->left;
else
current = current->right;
}
return current;
}
5)BST 最小值结点和最大值结点
最小值结点从左子树递归查找,最大值结点从右子树递归找。
/** * BST最小值结点 */
BTNode *bstMin(BTNode *root)
{
if (!root->left)
return root;
return bstMin(root->left);
}
/** * BST最大值结点 */
BTNode *bstMax(BTNode *root)
{
if (!root->right)
return root;
return bstMax(root->right);
}
6)二叉树结点数目和高度
/** * 二叉树结点数目 */
int btSize(BTNode *root)
{
if (!root) return 0;
return btSize(root->left) + btSize(root->right) + 1;
}
/** * 二叉树高度 */
int btHeight(BTNode *root)
{
if (!root) return 0;
int leftHeight = btHeight(root->left);
int rightHeight = btHeight(root->right);
int maxHeight = leftHeight > rightHeight ? leftHeight+1 : rightHeight+1;
return maxHeight;
}
3.二叉树遍历
递归遍历-先序、中序、后序、层
二叉树遍历的递归实现比较简单,直接给出代码。这里值得一提的是层序遍历,先是计算了二叉树的高度,然后调用的辅助函数依次遍历每一层的结点,这种方式比较容易理解,虽然在时间复杂度上会高一些。
/** * 二叉树先序遍历 */
void preOrder(BTNode *root)
{
if (!root) return;
printf("%d ", root->value);
preOrder(root->left);
preOrder(root->right);
}
/** * 二叉树中序遍历 */
void inOrder(BTNode *root)
{
if (!root) return;
inOrder(root->left);
printf("%d ", root->value);
inOrder(root->right);
}
/** * 二叉树后序遍历 */
void postOrder(BTNode *root)
{
if (!root) return;
postOrder(root->left);
postOrder(root->right);
printf("%d ", root->value);
}
/** * 二叉树层序遍历 */
void levelOrder(BTNode *root)
{
int btHeight = height(root);
int level;
for (level = 1; level <= btHeight; level++) {
levelOrderInLevel(root, level);
}
}
/** * 二叉树层序遍历辅助函数-打印第level层的结点 */
void levelOrderInLevel(BTNode *root, int level)
{
if (!root) return;
if (level == 1) {
printf("%d ", root->value);
return;
}
levelOrderInLevel(root->left, level-1);
levelOrderInLevel(root->right, level-1);
}
非递归遍历-先序、中序、后序、层序
- 非递归遍历里面先序遍历最简单,使用一个栈来保存结点,先访问根结点,然后将右孩子和左孩子依次压栈,然后循环这个过程。中序遍历稍微复杂一点,需要先遍历完左子树,然后才是根结点,最后才是右子树。
- 后序遍历使用一个栈的方法
postOrderIter()会有点绕,也易错。所以在面试时推荐用两个栈的版本postOrderIterWith2Stack(),容易理解,也比较好写。 - 层序遍历用了队列来辅助存储结点,还算简单。
- 这里我另外实现了一个队列
BTNodeQueue和栈BTNodeStack,用于二叉树非递归遍历。
/*********************/
/** 二叉树遍历-非递归 **/
/*********************/
/** * 先序遍历-非递归 */
void preOrderIter(BTNode *root)
{
if (!root) return;
int size = btSize(root);
BTNodeStack *stack = stackNew(size);
push(stack, root);
while (!IS_EMPTY(stack)) {
BTNode *node = pop(stack);
printf("%d ", node->value);
if (node->right)
push(stack, node->right);
if (node->left)
push(stack, node->left);
}
free(stack);
}
/** * 中序遍历-非递归 */
void inOrderIter(BTNode *root)
{
if (!root) return;
BTNodeStack *stack = stackNew(btSize(root));
BTNode *current = root;
while (current || !IS_EMPTY(stack)) {
if (current) {
push(stack, current);
current = current->left;
} else {
BTNode *node = pop(stack);
printf("%d ", node->value);
current = node->right;
}
}
free(stack);
}
/** * 后续遍历-使用一个栈非递归 */
void postOrderIter(BTNode *root)
{
BTNodeStack *stack = stackNew(btSize(root));
BTNode *current = root;
do {
// 移动至最左边结点
while (current) {
// 将该结点右孩子和自己入栈
if (current->right)
push(stack, current->right);
push(stack, current);
// 往左子树遍历
current = current->left;
}
current = pop(stack);
if (current->right && peek(stack) == current->right) {
pop(stack);
push(stack, current);
current = current->right;
} else {
printf("%d ", current->value);
current = NULL;
}
} while (!IS_EMPTY(stack));
}
/** * 后续遍历-使用两个栈,更好理解一点。 */
void postOrderIterWith2Stack(BTNode *root)
{
if (!root) return;
BTNodeStack *stack = stackNew(btSize(root));
BTNodeStack *output = stackNew(btSize(root));
push(stack, root);
BTNode *node;
while (!IS_EMPTY(stack)) {
node = pop(stack);
push(output, node);
if (node->left)
push(stack, node->left);
if (node->right)
push(stack, node->right);
}
while (!IS_EMPTY(output)) {
node = pop(output);
printf("%d ", node->value);
}
}
/** * 层序遍历-非递归 */
void levelOrderIter(BTNode *root)
{
if (!root) return;
BTNodeQueue *queue = queueNew(btSize(root));
enqueue(queue, root);
while (1) {
int nodeCount = QUEUE_SIZE(queue);
if (nodeCount == 0)
break;
btHeight
while (nodeCount > 0) {
BTNode *node = dequeue(queue);
printf("%d ", node->value);
if (node->left)
enqueue(queue, node->left);
if (node->right)
enqueue(queue, node->right);
nodeCount--;
}
printf("\n");
}
}
数据结构和算法面试题系列—二叉树面试题汇总
0.概述
继上一篇总结了二叉树的基础操作后,这一篇文章汇总下常见的二叉树相关面试题,主要分为判断类、构建类、存储类、查找类、距离类、混合类这六类大问题。本文所有代码在 这里 。
1.判断类问题
判断类问题主要分下下判断二叉树是否是二叉搜索树、二叉完全树,以及两棵二叉树是否同构这三个问题。
1.1 判断一棵二叉树是否是二叉搜索树(BST)
题: 给定一棵二叉树,判断该二叉树是否是二叉搜索树。
二叉搜索树是一种二叉树,但是它有附加的一些约束条件,这些约束条件必须对每个结点都成立:
- 结点的左子树所有结点的值都小于等于该结点的值。
- 结点的右子树所有结点的值都大于该结点的值。
- 结点的左右子树同样都必须是二叉搜索树。
一种错误解法
初看这个问题,容易这么实现:假定当前结点值为 k,对于二叉树中每个结点,判断其左孩子的值是否小于 k,其右孩子的值是否大于 k。如果所有结点都满足该条件,则该二叉树是一棵二叉搜索树。实现代码如下:
int isBSTError(BTNode *root)
{
if (!root) return 1;
if (root->left && root->left->value >= root->value)
return 0;
if (root->right && root->right->value < root->value)
return 0;
if (!isBSTError(root->left) || !isBSTError(root->right))
return 0;
return 1;
}
很不幸,这种做法是错误的,如下面这棵二叉树满足上面的条件,但是它并不是二叉搜索树。
10
/ \
5 15 -------- binary tree(1) 符合上述条件的二叉树,但是并不是二叉搜索树。
/ \
6 20
解1:蛮力法
上面的错误解法是因为判断不完整导致,可以这样来判断:
- 判断结点左子树最大值是否大于等于结点的值,如果是,则该二叉树不是二叉搜索树,否则继续下一步判断。。
- 判断右子树最小值是否小于或等于结点的值,如果是,则不是二叉搜索树,否则继续下一步判断。
- 递归判断左右子树是否是二叉搜索树。(代码中的
bstMax和bstMin函数功能分别是返回二叉树中的最大值和最小值结点,这里假定二叉树为二叉搜索树,实际返回的不一定是最大值和最小值结点)
int isBSTUnefficient(BTNode *root)
{
if (!root) return 1;
if (root->left && bstMax(root->left)->value >= root->value)
return 0;
if (root->right && bstMin(root->right)->value < root->value)
return 0;
if (!isBSTUnefficient(root->left) || !isBSTUnefficient(root->right))
return 0;
return 1;
}
解2:一次遍历法
以前面提到的 binary tree(1) 为例,当我们遍历到结点 15 时,我们知道右子树结点值肯定都 >=10。当我们遍历到结点 15 的左孩子结点 6 时,我们知道结点 15 的左子树结点值都必须在 10 到 15 之间。显然,结点 6 不符合条件,因此它不是一棵二叉搜索树。
int isBSTEfficient(BTNode* root, BTNode *left, BTNode *right)
{
if (!root) return 1;
if (left && root->value <= left->value)
return 0;
if (right && root->value > right->value)
return 0;
return isBSTEfficient(root->left, left, root) && isBSTEfficient(root->right, root, right);
}
解3:中序遍历解法
还可以模拟树的中序遍历来判断BST,可以直接将中序遍历的结果存到一个辅助数组,然后判断数组是否有序即可判断是否是BST。当然,我们可以不用辅助数组,在遍历时通过保留前一个指针 prev,据此来实现判断BST的解法,初始时 prev = NULL。
int isBSTInOrder(BTNode *root, BTNode *prev)
{
if (!root) return 1;
if (!isBSTInOrder(root->left, prev))
return 0;
if (prev && root->value < prev->value)
return 0;
return isBSTInOrder(root->right, root);
}
1.2 判断二叉树是否是完全二叉树
题: 给定一棵二叉树,判断该二叉树是否是完全二叉树(完全二叉树定义:若设二叉树的深度为 h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树,如下图所示)。
解1:常规解法-中序遍历
先定义一个 满结点 的概念:即一个结点存在左右孩子结点,则该结点为满结点。在代码中定义变量 flag 来标识是否发现非满结点,为1表示该二叉树存在非满结点。完全二叉树如果存在非满结点,则根据层序遍历队列中剩下结点必须是叶子结点,且如果一个结点的左孩子为空,则右孩子结点也必须为空。
int isCompleteBTLevelOrder(BTNode *root)
{
if (!root) return 1;
BTNodeQueue *queue = queueNew(btSize(root));
enqueue(queue, root);
int flag = 0;
while (QUEUE_SIZE(queue) > 0) {
BTNode *node = dequeue(queue);
if (node->left) {
if (flag) return 0;
enqueue(queue, node->left);
} else {
flag = 1;
}
if (node->right) {
if (flag) return 0;
enqueue(queue, node->right);
} else {
flag = 1;
}
}
return 1;
}
解2:更简单的方法-判断结点序号法
更简单的方法是判断结点序号法,因为完全二叉树的结点序号都是有规律的,如结点 i 的左右子结点序号为 2i+1 和 2i+2,如根结点序号是 0,它的左右子结点序号是 1 和 2 (如果都存在的话)。我们可以计算二叉树的结点数目,然后依次判断所有结点的序号,如果不是完全二叉树,那肯定会存在结点它的序号大于等于结点数目的。如前面提到的 binary tree(1) 就不是完全二叉树。
10(0)
/ \
5(1) 15(2) - 结点数目为5,如果是完全二叉树结点最大的序号应该是4,而它的是6,所以不是。
/ \
6(5) 20(6)
实现代码如下:
int isCompleteBTIndexMethod(BTNode *root, int index, int nodeCount)
{
if (!root) return 1;
if (index >= nodeCount)
return 0;
return (isCompleteBTIndexMethod(root->left, 2*index+1, nodeCount) &&
isCompleteBTIndexMethod(root->right, 2*index+2, nodeCount));
}
1.3 判断平衡二叉树
题: 判断一棵二叉树是否是平衡二叉树。所谓平衡二叉树,指的是其任意结点的左右子树高度之差不大于1。
__2__
/ \
1 4 ---- 平衡二叉树示例
\ / \
3 5 6
解1:自顶向下方法
判断一棵二叉树是否是平衡的,对每个结点计算左右子树高度差是否大于1即可,时间复杂度为O(N^2) 。
int isBalanceBTTop2Down(BTNode *root)
{
if (!root) return 1;
int leftHeight = btHeight(root->left);
int rightHeight = btHeight(root->right);
int hDiff = abs(leftHeight - rightHeight);
if (hDiff > 1) return 0;
return isBalanceBTTop2Down(root->left) && isBalanceBTTop2Down(root->right);
}
解2:自底向上方法
因为解1会重复的遍历很多结点,为此我们可以采用类似后序遍历的方式,自底向上来判断左右子树的高度差,这样时间复杂度为 O(N)。
int isBalanceBTDown2Top(BTNode *root, int *height) {
if (!root) {
*height = 0;
return 1;
}
int leftHeight, rightHeight;
if (isBalanceBTDown2Top(root->left, &leftHeight) &&
isBalanceBTDown2Top(root->right, &rightHeight)) {
int diff = abs(leftHeight - rightHeight);
return diff > 1 ? 0 : 1;
}
return 0;
}
1.4 判断两棵二叉树是否同构
题: 给定两棵二叉树,根结点分别为 t1 和 t2,判定这两棵二叉树是否同构。所谓二叉树同构就是指它们的结构相同,如下二叉树 (1) 和 (2) 是同构的,而它们和 (3) 是不同结构的:
5 9 6
/ \ / \ / \
1 2 7 12 5 9
/ \ / \ \
4 3 5 8 10
二叉树(1) 二叉树(2) 二叉树(3)
解: 二叉树结构是否相同,还是递归实现,先判断根结点是否同构,然后再判断左右子树。
int isOmorphism(BTNode *t1, BTNode *t2)
{
if (!t1 || !t2)
return (!t1) && (!t2);
return isOmorphism(t1->left, t2->left) && isOmorphism(t1->right, t2->right);
}
2.构建类问题
构建类问题主要是使用二叉树的两种遍历顺序来确定二叉树的另外一种遍历顺序问题。在上一篇文章中我们分析过二叉树的先序、中序、后序遍历的递归和非递归实现。那么,是否可以根据先序、中序或者先序、后序或者中序、后序唯一确定一棵二叉树呢?
答案是 在没有重复值的二叉树中, 根据先序遍历和后序遍历无法唯一确定一棵二叉树,而根据先序、中序或者中序、后序遍历是可以唯一确定一棵二叉树的。
1)先序和后序遍历无法唯一确定一棵二叉树
一个简单的例子如下,这两棵二叉树的先序遍历和后序遍历相同,由此可以证明先序遍历和后序遍历无法唯一确定一棵二叉树。
1 1
/ / 2 2 \ /
3 3
先序遍历: 1 2 3
后序遍历: 3 2 1
2)先序和中序遍历可以唯一确定二叉树
简单证明:因为先序遍历的第一个元素是根结点,该元素将二叉树中序遍历序列分成两部分,左边(假设有 L 个元素)表示左子树,若左边无元素,则说明左子树为空;右边(假设有R个元素)是右子树,若为空,则右子树为空。根据前序遍历中”根-左子树-右子树”的顺序,则由从先序序列的第二元素开始的 L 个结点序列和中序序列根左边的 L 个结点序列构造左子树,由先序序列最后 R 个元素序列与中序序列根右边的 R 个元素序列构造右子树。
3)中序和后序遍历可以唯一确定二叉树
简单证明: 假定二叉树结点数为 n,假定中序遍历为 S1, S2, …, Sn,而后序遍历为 P1, P2, …, Pn,因为后序遍历最后一个结点 Pn 是根结点,则可以根据 Pn 将中序遍历分为两部分,则其中左边 L 个结点是左子树结点,右边 R 个结点是右子树结点,则后序遍历中的 1~L 个结点是左子树的后序遍历,由此 PL 是左子树的根,与前面同理可以将中序遍历分成两部分,直到最终确定该二叉树。
2.1 根据先序、中序遍历构建二叉树
题: 给定一棵二叉树的先序和中序遍历序列,请构建该二叉树(注:二叉树没有重复的值)。
先序遍历: 7 10 4 3 1 2 8 11
中序遍历: 4 10 3 1 7 11 8 2
二叉树如下:
7 / \ 10 2 / \ / 4 3 8 \ / 1 11
解: 根据前面的分析来解这个问题。
- 先序遍历的第一个结点总是根结点。如上图中的二叉树,根结点为 7 。
- 可以观察到在中序遍历中,根结点 7 是第 4 个值(从 0 开始算起)。由于中序遍历顺序为:左子树,根结点,右子树。所以根结点7左边的
{4,10,3,1}这四个结点属于左子树,而根结点7右边的{11,8,2}属于右子树。 - 据此可以写出递归式了。注意关于如何得到根结点在中序遍历中的位置代码中使用线性扫描查找位置,每次查找需要
O(N)的时间,整个算法需要O(N^2)的时间。如果要提高效率,也可以哈希表来存储与查找根结点在中序遍历中的位置,每次查找只需要O(1)的时间,这样构建整棵树只需要O(N)的时间。 - 调用方法为
buildBTFromPreInOrder(preorder, inorder, n, 0, n);,其中preorder和inorder分别为先序中序遍历数组,n为数组大小。
/**
* 辅助函数,查找根结点在中序遍历中的位置。
*/
int findBTRootIndex(int inorder[], int count, int rootVal)
{
int i;
for (i = 0; i < count; i++) {
if (inorder[i] == rootVal)
return i;
}
return -1;
}
/**
/**
* 根据先序和中序遍历构建二叉树
*/
BTNode *buildBTFromPreInOrder(int preorder[], int inorder[], int n, int offset, int count)
{
if (n == 0) return NULL;
int rootVal = preorder[0];
int rootIndex = findBTRootIndex(inorder, count, rootVal);
int leftCount = rootIndex - offset; // 左子树结点数目
int rightCount = n - leftCount - 1; // 右子树结点数目
BTNode *root = btNewNode(rootVal);
root->left = buildBTFromPreInOrder(preorder+1, inorder, leftCount, offset, count);
root->right = buildBTFromPreInOrder(preorder+leftCount+1, inorder, rightCount, offset+leftCount+1, count);
return root;
}
根据中序、后序遍历构建二叉树
题: 给定一棵二叉树的中序和后序遍历序列,请构建该二叉树(注:二叉树没有重复的值)。
中序遍历: 4 10 3 1 7 11 8 2
后序遍历: 4 1 3 10 11 8 2 7
二叉树如下:
7 / \ 10 2 / \ / 4 3 8 \ / 1 11 解: 跟前面一题类似,只是这里根结点是从后序遍历数组的最后一个元素取。
/**
* 根据中序和后序遍历构建二叉树
*/
BTNode *buildBTFromInPostOrder(int postorder[], int inorder[], int n, int offset, int count)
{
if (n == 0) return NULL;
int rootVal = postorder[n-1];
int rootIndex = findBTRootIndex(inorder, count, rootVal);
int leftCount = rootIndex - offset; // 左子树结点数目
int rightCount = n - leftCount - 1; // 右子树结点数目
BTNode *root = btNewNode(rootVal);
root->left = buildBTFromInPostOrder(postorder, inorder, leftCount, offset, count);
root->right = buildBTFromInPostOrder(postorder+leftCount, inorder, rightCount, offset+leftCount+1, count);
return root;
}
3.存储类问题
3.1 二叉搜索树存储和恢复
题: 设计一个算法,将一棵二叉搜索树(BST)保存到文件中,需要能够从文件中恢复原来的二叉搜索树,注意算法的时空复杂度。
30 / \ 20 40 / / \ 10 35 50 思路
二叉树遍历算法有先序遍历、中序遍历、后序遍历算法等。但是它们中间哪一种能够用于保存BST到文件中并从文件中恢复原来的BST,这是个要考虑的问题。
假定用中序遍历,因为这棵BST的中序遍历为 10 20 30 35 40 50,可能的结构是下面这样,因此 中序遍历不符合要求 。
50
/
40
/
35
/
30
/
20
/
10
既然中序遍历不行,后序遍历如何?后序遍历该BST可以得到:10 20 35 50 40 30 。读取这些结点并构造出原来的BST是个难题,因为在构造二叉树时是先构造父结点再插入孩子结点,而后序遍历序列是先读取到孩子结点然后才是父结点,所以 后续遍历也不符合条件 。
综合看来,只有先序遍历满足条件 。该BST的先序遍历是 30 20 10 40 35 50 。我们观察到重要的一点就是:一个结点的父亲结点总是在该结点之前输出 。有了这个观察,我们从文件中读取BST结点序列后,总是可以在构造孩子结点之前构造它们的父结点。将BST写入到文件的代码跟先序遍历一样。
那么读取恢复怎么做呢?使用二叉搜索树 bstInsert() 方法执行 N 次插入操作即可,如果二叉搜索树平衡的话每次插入需要时间 O(lgN),共需要 O(NlgN) 的时间,而最坏情况下为 O(N^2)。
/** * 存储二叉树到文件中-使用先序遍历 */
void bstSave(BTNode *root, FILE *fp)
{
if (!root) return;
char temp[30];
sprintf(temp, "%d\n", root->value);
fputs(temp, fp);
bstSave(root->left, fp);
bstSave(root->right, fp);
}
/** * 从文件中恢复二叉树 */
BTNode *bstRestore(FILE *fp)
{
BTNode *root = NULL;
char *s;
char buf[30];
while ((s = fgets(buf, 30, fp))) {
int nodeValue = atoi(s);
root = bstInsert(root, nodeValue);
}
return root;
}
3.2 二叉树存储和恢复
题: 设计一个算法能够实现二叉树(注意,不是二叉搜索树BST)存储和恢复。
解: 3.1节提到过使用先序遍历可以保存和恢复二叉搜索树,而这个题目是针对二叉树,并不是BST,所以不能用前面的方式。不过,我们可以采用先序遍历的思想,只是在这里需要改动。为了能够在重构二叉树时结点能够插入到正确的位置,在使用先序遍历保存二叉树到文件中的时候需要把 NULL 结点也保存起来(可以使用特殊符号如 # 来标识 NULL 结点)。
注意: 本题采用 # 保存 NULL 结点的方法存在缺陷,如本方法中二叉树结点值就不能是 #。如果要能保存各种字符,则需要采用其他方法来实现了。
30 / \ 10 20 / / \ 50 45 35 如上面这棵二叉树,保存到文件中则为 30 10 50 # # # 20 45 # # 35 # #。于是,保存和恢复实现的代码如下:
/** * 存储二叉树到文件中 */
void btSave(BTNode *root, FILE *fp)
{
if (!root) {
fputs("#\n", fp);
} else {
char temp[30];
sprintf(temp, "%d\n", root->value);
fputs(temp, fp);
btSave(root->left, fp);
btSave(root->right, fp);
}
}
/** * 从文件恢复二叉树 */
BTNode *btRestore(BTNode *root, FILE *fp)
{
char buf[30];
char *s = fgets(buf, 30, fp);
if (!s || strcmp(s, "#\n") == 0)
return NULL;
int nodeValue = atoi(s);
root = btNewNode(nodeValue);
root->left = btRestore(root->left, fp);
root->right = btRestore(root->right, fp);
return root;
}
4.查找类问题
查找类问题主要包括:查找二叉树/二叉搜索树的最低公共祖先结点,或者是二叉树中的最大的子树且该子树为二叉搜索树等。
4.1 二叉搜索树最低公共祖先结点
题: 给定一棵二叉搜索树( BST ),找出树中两个结点的最低公共祖先结点( LCA )。如下面这棵二叉树结点 2 和 结点 8 的 LCA 是 6,而结点 4 和 结点 2 的 LCA 是 2。
______6______ / \ __2__ __8__ / \ / \ 0 4 7 9 / \ 3 5
解: 我们从顶往下遍历二叉搜索树时,对每个遍历到的结点,待求 LCA 的两个结点可能有如下四种分布情况:
- 1)两个结点都在树的左子树中: LCA一定在当前遍历结点的左子树中。
- 2)两个结点都在树的右子树中: LCA一定在当前遍历结点右子树中。
- 3)一个结点在树的左边,一个结点在树的右边: LCA就是当前遍历的结点。
- 4)当前结点等于这两个结点中的一个: LCA也是当前遍历的结点。
BTNode *bstLCA(BTNode *root, BTNode *p, BTNode *q)
{
if (!root || !p || !q) return NULL;
int maxValue = p->value >= q->value ? p->value : q->value;
int minValue = p->value < q->value ? p->value : q->value;
if (maxValue < root->value) {
return bstLCA(root->left, p, q);
} else if (minValue > root->value) {
return bstLCA(root->right, p, q);
} else {
return root;
}
}
4.2 二叉树(不一定是 BST )最低公共祖先结点
题: 给定二叉树中的两个结点,输出这两个结点的最低公共祖先结点(LCA)。注意,该二叉树不一定是二叉搜索树。
_______3______ / \ ___5__ ___1__ / \ / \ 6 2 0 8 / \ 7 4 解1:自顶向下方法
因为不一定是BST,所以不能根据值大小来判断,不过总体思路是一样的:我们可以从根结点出发,判断当前结点的左右子树是否包含这两个结点。
- 如果左子树包含两个结点,则它们的最低公共祖先结点也一定在左子树中。
- 如果右子树包含两个结点,则它们的最低公共祖先结点也一定在右子树中。
- 如果一个结点在左子树,而另一个结点在右子树中,则当前结点就是它们的最低公共祖先结点。
因为对每个结点都要重复判断结点 p 和 q 的位置,总的时间复杂度为 O(N^2),为此,我们可以考虑找一个效率更高的方法。
/** * 二叉树最低公共祖先结点-自顶向下解法 O(N^2) */
BTNode *btLCATop2Down(BTNode *root, BTNode *p, BTNode *q)
{
if (!root || !p || !q) return NULL;
if (btExist(root->left, p) && btExist(root->left, q)) {
return btLCATop2Down(root->left, p, q);
} else if (btExist(root->right, p) && btExist(root->right, q)) {
return btLCATop2Down(root->right, p, q);
} else {
return root;
}
}
/** * 二叉树结点存在性判断 */
int btExist(BTNode *root, BTNode *node)
{
if (!root) return 0;
if (root == node) return 1;
return btExist(root->left, node) || btExist(root->right, node);
}
解2:自底向上方法
因为自顶向下方法有很多重复的判断,于是有了这个自底向上的方法。自底向上遍历结点,一旦遇到结点等于 p 或者 q,则将其向上传递给它的父结点。父结点会判断它的左右子树是否都包含其中一个结点,如果是,则父结点一定是这两个结点 p 和 q 的 LCA。如果不是,我们向上传递其中的包含结点 p 或者 q 的子结点,或者 NULL (如果左右子树都没有结点 p 或 q )。该方法时间复杂度为 O(N)。
/** * 二叉树最低公共祖先结点-自底向上解法 O(N) */
BTNode *btLCADown2Top(BTNode *root, BTNode *p, BTNode *q)
{
if (!root) return NULL;
if (root == p || root == q) return root;
BTNode *left = btLCADown2Top(root->left, p, q);
BTNode *right = btLCADown2Top(root->right, p, q);
if (left && right)
return root; // 如果p和q位于不同的子树
return left ? left: right; //p和q在相同的子树,或者p和q不在子树中
}
4.3 二叉树的最大二叉搜索子树
题: 找出二叉树中最大的子树,该子树为二叉搜索树。所谓最大的子树就是指结点数目最多的子树。
___10___
/ \
_5_ 15
/ \ \
1 8 7
___10____
/ \
_5_ 15 -------- subtree (1)
/ \
1 8
_5_
/ \ -------- subtree (2)
1 8
根据维基百科对 子树 的定义,一棵二叉树T的子树由T的某个结点和该结点所有的后代构成。也就是说,该题目中,subtree(2) 才是正确的答案,因为 subtree(1) 不包含结点7,不满足子树的定义。
解1:自顶向下解法
最自然的解法是以根结点开始遍历二叉树所有的结点,判定以当前结点为根的子树是否是BST,如果是,则该结点为根的BST就是最大的BST。如果不是,递归调用左右子树,返回其中包含较多结点的子树。
/**
* 查找二叉树最大的二叉搜索子树-自顶向下方法
*/
BTNode *largestSubBSTTop2Down(BTNode *root, int *bstSize)
{
if (!root) {
*bstSize = 0;
return NULL;
}
if (isBSTEfficient(root, NULL, NULL)) { //以root为根结点的树为BST,则设置结果为root并返回。
*bstSize = btSize(root);
return root;
}
int lmax, rmax;
BTNode *leftBST = largestSubBSTTop2Down(root->left, &lmax); //找出左子树中为BST的最大的子树
BTNode *rightBST = largestSubBSTTop2Down(root->right, &rmax); //找出右子树中为BST的最大的子树
*bstSize = lmax > rmax ? lmax : rmax; //设定结点最大数目
BTNode *result = lmax > rmax ? leftBST : rightBST;
return result;
}
解2:自底向上解法
自顶向下的解法时间复杂度为 O(N^2),每个结点都要判断是否满足BST的条件,可以用从底向上方法优化。我们在判断上面结点为根的子树是否是BST之前已经知道底部结点为根的子树是否是BST,因此只要以底部结点为根的子树不是BST,则以它上面结点为根的子树一定不是BST。我们可以记录子树包含的结点数目,然后跟父结点所在的二叉树比较,来求得最大BST子树。
/**
* 查找二叉树最大的二叉搜索子树-自底向上方法
*/
BTNode *largestSubBSTDown2Top(BTNode *root, int *bstSize)
{
BTNode *largestBST = NULL;
int min, max, maxNodes=0;
findLargestSubBST(root, &min, &max, &maxNodes, &largestBST);
*bstSize = maxNodes;
return largestBST;
}
/**
* 查找最大二叉搜索子树自底向上方法主体函数
* 如果是BST,则返回BST的结点数目,否则返回-1
*/
int findLargestSubBST(BTNode *root, int *min, int *max, int *maxNodes, BTNode **largestSubBST)
{
if (!root) return 0;
int isBST = 1;
int leftNodes = findLargestSubBST(root->left, min, max, maxNodes, largestSubBST);
int currMin = (leftNodes == 0) ? root->value : *min;
if (leftNodes == -1 || (leftNodes != 0 && root->value <= *max))
isBST = 0;
int rightNodes = findLargestSubBST(root->right, min, max, maxNodes, largestSubBST);
int currMax = (rightNodes == 0) ? root->value : *max;
if (rightNodes == -1 || (rightNodes != 0 && root->value > *min))
isBST = 0;
if (!isBST)
return -1;
*min = currMin;
*max = currMax;
int totalNodes = leftNodes + rightNodes + 1;
if (totalNodes > *maxNodes) {
*maxNodes = totalNodes;
*largestSubBST = root;
}
return totalNodes;
}
5.距离类问题
5.1 二叉树两个结点之间的最短距离
题: 已知二叉树中两个结点,求这两个结点之间的最短距离(注:最短距离是指从一个结点到另一个结点需要经过的边的条数)。
___1___
/ \
2 3
/ \ / \
4 5 6 7
\
8
Distance(4, 5) = 2
Distance(4, 6) = 4
Distance(3, 4) = 3
Distance(2, 4) = 1
Distance(8, 5) = 5
解: 两个结点的距离比较好办,先求出两个结点的最低公共祖先结点(LCA),然后计算 LCA 到两个结点的距离之和即可,时间复杂度 O(N) 。
/**
* 计算二叉树两个结点最短距离
*/
int distanceOf2BTNodes(BTNode *root, BTNode *p, BTNode *q)
{
if (!root) return 0;
BTNode *lca = btLCADown2Top(root, p, q);
int d1 = btDistanceFromRoot(lca, p, 0);
int d2 = btDistanceFromRoot(lca, q, 0);
return d1+d2;
}
/**
* 计算二叉树结点node和root的距离
*/
int btDistanceFromRoot(BTNode *root, BTNode *node, int level)
{
if (!root) return -1;
if (root == node) return level;
int left = btDistanceFromRoot(root->left, node, level+1);
if (left == -1)
return btDistanceFromRoot(root->right, node, level+1);
return left;
}
5.2 二叉搜索树两个结点的最短距离
题: 求一棵二叉搜索树中的两个结点的最短距离。
解: 与前面不同的是,这是一棵 BST,那么我们可以使用二叉搜索树的特点来简化距离计算流程,当然直接用 5.1 的方法是完全 OK 的,因为它是通用的计算方法。
/** * 计算BST两个结点最短距离。 */
int distanceOf2BSTNodes(BTNode *root, BTNode *p, BTNode *q)
{
if (!root) return 0;
if (root->value > p->value && root->value > q->value) {
return distanceOf2BSTNodes(root->left, p, q);
} else if(root->value <= p->value && root->value <= q->value){
return distanceOf2BSTNodes(root->right, p, q);
} else {
return bstDistanceFromRoot(root, p) + bstDistanceFromRoot(root, q);
}
}
/** * 计算BST结点node和root的距离 */
int bstDistanceFromRoot(BTNode *root, BTNode *node)
{
if (root->value == node->value)
return 0;
else if (root->value > node->value)
return 1 + bstDistanceFromRoot(root->left, node);
else
return 1 + bstDistanceFromRoot(root->right, node);
}
5.3 二叉树中结点的最大距离
题: 写一个程序求一棵二叉树中相距最远的两个结点之间的距离。
解: 《编程之美》上有这道题,这题跟前面不同,要求相距最远的两个结点的距离,而且并没有指定两个结点位置。计算一个二叉树的最大距离有两个情况:
- 1)路径为 左子树的最深节点 -> 根节点 -> 右子树的最深节点。
- 2)路径不穿过根节点,而是左子树或右子树的最大距离路径,取其大者。
___10___
/ \
_5_ 15 ------ 第1种情况
/ \ \
1 8 7
10
/
5
/ \ ------ 第2种情况
1 8
/ \
2 3
我们定义函数 maxDistanceOfBT(BTNode *root) 用于计算二叉树相距最远的两个结点的距离,可以递归的先计算左右子树的最远结点距离,然后比较左子树最远距离、右子树最远距离以及左右子树最大深度之和,从而求出整个二叉树的相距最远的两个结点的距离。
int btMaxDistance(BTNode *root, int *maxDepth)
{
if (!root) {
*maxDepth = 0;
return 0;
}
int leftMaxDepth, rightMaxDepth;
int leftMaxDistance = btMaxDistance(root->left, &leftMaxDepth);
int rightMaxDistance = btMaxDistance(root->right, &rightMaxDepth);
*maxDepth = max(leftMaxDepth+1, rightMaxDepth+1);
int maxDistance = max3(leftMaxDistance, rightMaxDistance, leftMaxDepth+rightMaxDepth); // max求两个数最大值,max3求三个数最大值,详见代码
return maxDistance;
}
5.4 二叉树最大宽度
题: 给定一棵二叉树,求该二叉树的最大宽度。二叉树的宽度指的是每一层的结点数目。如下面这棵二叉树,从上往下 1 – 4 层的宽度分别是 1,2,3,2,于是它的最大宽度为 3。
1 / \ 2 3 / \ \ 4 5 8 / \ 6 7 解1:层序遍历法
最容易想到的方法就是使用层序遍历,然后计算每一层的结点数,然后得出最大结点数。该方法时间复杂度为 O(N^2)。当然如果优化为使用队列来实现层序遍历,可以得到 O(N) 的时间复杂度。
/**
* 二叉树最大宽度
*/
int btMaxWidth(BTNode *root)
{
int h = btHeight(root);
int level, width;
int maxWidth = 0;
for (level = 1; level <= h; level++) {
width = btLevelWidth(root, level);
if (width > maxWidth)
maxWidth = width;
}
return maxWidth;
}
/**
* 二叉树第level层的宽度
*/
int btLevelWidth(BTNode *root, int level)
{
if (!root) return 0;
if (level == 1) return 1;
return btLevelWidth(root->left, level-1) + btLevelWidth(root->right, level-1);
}
解2:先序遍历法
我们可以先创建一个大小为二叉树高度 h 的辅助数组来存储每一层的宽度,初始化为 0。通过先序遍历的方式来遍历二叉树,并设置好每层的宽度。最后,从这个辅助数组中求最大值即是二叉树最大宽度。
/**
* 二叉树最大宽度-先序遍历法
*/
int btMaxWidthPreOrder(BTNode *root)
{
int h = btHeight(root);
int *count = (int *)calloc(sizeof(int), h);
btLevelWidthCount(root, 0, count);
int i, maxWidth = 0;
for (i = 0; i < h; i++) {
if (count[i] > maxWidth)
maxWidth = count[i];
}
return maxWidth;
}
/**
* 计算二叉树从 level 开始的每层宽度,并存储到数组 count 中。
*/
void btLevelWidthCount(BTNode *root, int level, int count[])
{
if (!root) return;
count[level]++;
btLevelWidthCount(root->left, level+1, count);
btLevelWidthCount(root->right, level+1, count);
}
6.混合类问题
此类问题主要考察二叉树和链表/数组等结合,形式偏新颖。
6.1 根据有序数组构建平衡二叉搜索树
题: 给定一个有序数组,数组元素升序排列,试根据该数组元素构建一棵平衡二叉搜索树(Balanced Binary Search Tree)。所谓平衡的定义,就是指二叉树的子树高度之差不能超过1。
__3__
/ \
1 5 ---- 平衡二叉搜索树示例
\ / \
2 4 6
解: 如果要从一个有序数组中选择一个元素作为根结点,应该选择哪个元素呢?我们应该选择有序数组的中间元素作为根结点。选择了中间元素作为根结点并创建后,剩下的元素分为两部分,可以看作是两个数组。这样剩下的元素在根结点左边的作为左子树,右边的作为右子树。
BTNode *sortedArray2BST(int a[], int start, int end)
{
if (start > end) return NULL;
int mid = start + (end-start)/2;
BTNode *root = btNewNode(a[mid]);
root->left = sortedArray2BST(a, start, mid-1);
root->right = sortedArray2BST(a, mid+1, end);
return root;
}
6.2 有序单向链表构建平衡二叉搜索树
题: 给定一个有序的单向链表,构建一棵平衡二叉搜索树。
解: 最自然的想法是先将链表中的结点的值保存在数组中,然后采用 6.1 中方法实现,时间复杂度为 O(N)。我们还可以采用自底向上的方法,在这里我们不再需要每次查找中间元素。
下面代码依旧需要链表长度作为参数,计算链表长度时间复杂度为 O(N),算法时间复杂度也为 O(N),所以总的时间复杂度为 O(N)。代码中需要注意的是每次调用 sortedList2BST 函数时,list 位置都会变化,调用完函数后 list 总是指向 mid+1 的位置 (如果满足返回条件,则 list 位置不变)。
BTNode *sortedList2BST(ListNode **pList, int start, int end)
{
if (start > end) return NULL;
int mid = start + (end-start)/2;
BTNode *left = sortedList2BST(pList, start, mid-1);
BTNode *parent = btNewNode((*pList)->value);
parent->left = left;
*pList = (*pList)->next;
parent->right = sortedList2BST(pList, mid+1, end);
return parent;
}
例如链表只有 2 个节点 3->5->NULL,则初始 start=0, end=1, mid=0,继而递归调用 sortedList2BST(pList, start,mid-1),此时直接返回 NULL。即左孩子为NULL, 根结点为 3,而后链表指向 5,再调用 sortedList2BST(pList, mid+1, end),而这次调用返回结点 5,将其赋给根结点 3 的右孩子。这次调用的 mid=1,调用完成后 list 已经指向链表末尾。
6.3 二叉搜索树转换为有序循环链表
题: 给定一棵二叉搜索树( BST ),将其转换为双向的有序循环链表。

解: 如图所示,需要将 BST 的左右孩子指针替换成链表的 prev 和 next 指针,分别指向双向链表的前一个和后一个结点。相信大多数人第一反应就是中序遍历这棵二叉树,同时改变树中结点的 left 和 right 指针。这里需要额外考虑的是如何将最后一个结点的right 指针指向第一个结点,如下图所展示的那样。

以中序遍历遍历一棵二叉树的时候,每遍历到一个结点,我们就可以修改该结点的 left 指针指向前一个遍历到的结点,因为在后续操作中我们不会再用到 left 指针;与此同时,我们还需要修改前一个遍历结点的 right 指针,让前一个遍历结点的 right 指针指向当前结点。比如我们遍历到结点 2,则我们修改结点2的 left 指针指向结点 1,同时需要修改结点 1 的 right 指针指向结点 2。需要注意一点,这里的前一个遍历结点不是当前结点的父结点,而是当前结点的前一个比它小的结点。
看似问题已经解决,慢着,我们其实落下了重要的两步。1)我们没有对头结点head赋值。 2)最后一个结点的right指针没有指向第一个结点。
解决这两个问题的方案非常简单:在每次递归调用的时候,更新当前遍历结点的 right 指针让其指向头结点 head,同时更新头结点 head 的 left 指针让其指向当前遍历结点。当递归调用结束的时候,链表的头尾结点会指向正确的位置。不要忘记只有一个结点的特殊情况,它的 left 和 right 指针都是指向自己。

void bt2DoublyList(BTNode *node, BTNode **pPrev, BTNode **pHead)
{
if (!node) return;
bt2DoublyList(node->left, pPrev, pHead);
// 当前结点的left指向前一个结点pPrev
node->left = *pPrev;
if (*pPrev)
(*pPrev)->right = node; // 前一个结点的right指向当前结点
else
*pHead = node; // 如果前面没有结点,则设置head为当前结点(当前结点为最小的结点)。
// 递归结束后,head的left指针指向最后一个结点,最后一个结点的右指针指向head结点。
// 注意保存当前结点的right指针,因为在后面代码中会修改该指针。
BTNode *right = node->right;
(*pHead)->left = node;
node->right = (*pHead);
*pPrev = node;//更新前一个结点
bt2DoublyList(right, pPrev, pHead);
}
这个解法非常的精巧,因为该算法是对中序遍历的一个改进,因此它的时间复杂度为 O(N),N 为结点数目。当然,相比中序遍历,我们在每次递归调用过程中增加了额外的赋值操作。
系列文章目录
- 0. 数据结构和算法面试题系列—C指针、数组和结构体
- 1. 数据结构和算法面试题系列—字符串
- 2. 数据结构和算法面试题系列—链表
- 3. 数据结构和算法面试题系列—栈
- 4. 数据结构和算法面试题系列—二叉堆
- 5. 数据结构和算法面试题系列—二叉树基础
- 6. 数据结构和算法面试题系列—二叉树面试题汇总
- 7. 数据结构和算法面试题系列—二分查找算法详解
- 8. 数据结构和算法面试题系列—排序算法之基础排序
- 9. 数据结构和算法面试题系列—排序算法之快速排序
- 10. 数据结构和算法面试题系列—随机算法总结
- 11. 数据结构和算法面试题系列—递归算法总结
- 12. 数据结构和算法面试题系列—背包问题总结
- 13. 数据结构和算法面试题系列—数字题总结
其他
此外,在我 简书的博客 上还整理有《docker相关技术笔记》、《MIT6.828操作系统学习笔记》、《python源码剖析笔记》等文章,请大家指正。
参考资料
- 《c专家编程》
- 《linux c一站式编程》
- 《高质量C/C++编程》
- 结构体字节对齐
- 柔性数组
- Sliding Window Maximum – LeetCode
- Longest Palindromic Substring – LeetCode
- 编程珠玑
- 算法导论
- MIT6.828代码
- Detect loop in a linked list – GeeksforGeeks
- 判断单链表是否存在环,判断两个链表是否相交问题详解
- Find first node of loop in a linked list – GeeksforGeeks
- Merge two sorted linked list without duplicates – GeeksforGeeks
- Stack Implementation in C – Techie Delight
- Stack | Set 4 (Evaluation of Postfix Expression) – GeeksforGeeks
- Reverse a stack using recursion – GeeksforGeeks
- 算法导论第6章《堆排序》
- Insertion in BST | Recursive & Iterative Solution – Techie Delight
- Search given key in BST | Recursive & Iterative Solution – Techie Delight
- Iterative Postorder Traversal | Set 2 (Using One Stack) – GeeksforGeeks
- A program to check if a binary tree is BST or not – GeeksforGeeks
- Check whether a given Binary Tree is Complete or not | Set 1 (Iterative Solution) – GeeksforGeeks
- Check whether a binary tree is a complete tree or not | Set 2 (Recursive Solution) – GeeksforGeeks
- Serialization/Deserialization of a Binary Tree – LeetCode
- Lowest Common Ancestor of a Binary Search Tree (BST) – LeetCode
- Largest Subtree Which is a Binary Search Tree (BST) – LeetCode
- Find distance between two nodes of a Binary Tree – GeeksforGeeks
- Shortest distance between two nodes in BST – GeeksforGeeks
- Maximum width of a binary tree – GeeksforGeeks
- Convert Sorted List to Balanced Binary Search Tree (BST) – LeetCode
- Convert Binary Search Tree (BST) to Sorted Doubly-Linked List – LeetCode
- 程序员面试题精选100题(60)-判断二叉树是不是平衡[数据结构]
我在参加掘金技术征文 活动详情 秋招求职时,写文就有好礼相送 | 掘金技术征文

今天的文章那些年,面试中常见的数据结构基础和算法题(上) | 掘金技术征文分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:http://bianchenghao.cn/18719.html
