【算法】前端遇到的广度/深度优先搜索

前言

在面试或者技术社区冲浪的时候，一不小心就会看到深度优先搜索、广度优先搜索这两个概念，这一次在项目中一个需求用到了相关的知识，故此在这里通过理论+实际来总结一下。

1. 示例

下面一张图可以比较理解两者的差异：

为了后面好操作，我们先定义一组平行节点为以下，假想有一个共同的根节点：

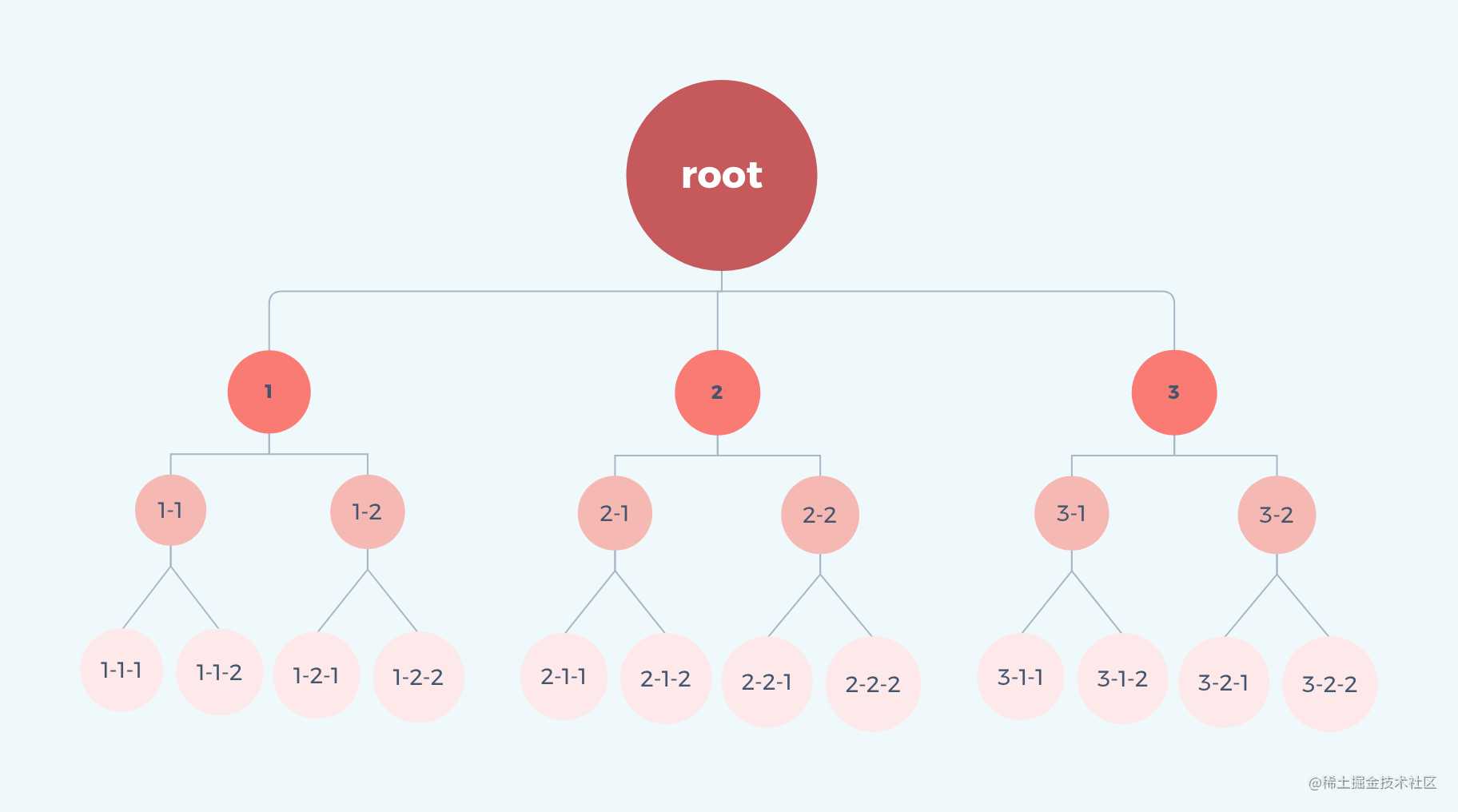
const root = [ { id: '1', children: [ { id: '1-1', children: [{ id: '1-1-1' }, { id: '1-1-2' }],
      },
      {
        id: '1-2',
        children: [{ id: '1-2-1' }, { id: '1-2-2' }],
      },
    ],
  },
  {
    id: '2',
    children: [
      {
        id: '2-1',
        children: [{ id: '2-1-1' }, { id: '2-1-2' }],
      },
      {
        id: '2-2',
        children: [{ id: '2-2-1' }, { id: '2-2-2' }],
      },
    ],
  },
  {
    id: '3',
    children: [
      {
        id: '3-1',
        children: [{ id: '3-1-1' }, { id: '3-1-2' }],
      },
      {
        id: '3-2',
        children: [{ id: '3-2-1' }, { id: '3-2-2' }],
      },
    ],
  },
];

const target = '2-2-2';

2. 深度优先搜索

深度优先搜索（depth first search），从图中也可以看出来，是从根节点开始，沿树的深度进行搜索，尽可能深的搜索分支。当节点所在的边都已经搜多过，则回溯到上一个节点，再搜索其余的边。

深度优先搜索采用栈结构，后进先出。

算法：

js 递归实现和非递归实现：

const depthFirstSearchWithRecursive = source => {
  const result = []; // 存放结果的数组
  // 递归方法
  const dfs = data => {
    // 遍历数组
    data.forEach(element => {
      // 将当前节点 id 存放进结果
      result.push(element.id);
      // 如果当前节点有子节点，则递归调用
      if (element.children && element.children.length > 0) {
        dfs(element.children);
      }
    });
  };
  // 开始搜索
  dfs(source);
  return result;
};

const depthFirstSearchWithoutRecursive = source => {
  const result = []; // 存放结果的数组
  // 当前栈内为全部数组
  const stack = JSON.parse(JSON.stringify(source));
  // 循环条件，栈不为空
  while (stack.length !== 0) {
    // 最上层节点出栈
    const node = stack.shift();
    // 存放节点
    result.push(node.id);
    // 如果该节点有子节点，将子节点存入栈中，继续下一次循环
    const len = node.children && node.children.length;
    for (let i = len - 1; i >= 0; i -= 1) {
      stack.unshift(node.children[i]);
    }
  }
  return result;
};

3. 广度优先搜索

广度优先搜索（breadth first search），从图中也可以看出来，是从根节点开始，沿树的宽度进行搜索，如果所有节点都被访问，则算法中止。

广度优先搜索采用队列的形式，先进先出。

js 实现：

const breadthFirstSearch = source => {
  const result = []; // 存放结果的数组
  // 当前队列为全部数据
  const queue = JSON.parse(JSON.stringify(source));
  // 循环条件，队列不为空
  while (queue.length > 0) {
    // 第一个节点出队列
    const node = queue.shift();
    // 存放结果数组
    result.push(node.id);
    // 当前节点有子节点则将子节点存入队列，继续下一次的循环
    const len = node.children && node.children.length;
    for (let i = 0; i < len; i += 1) {
      queue.push(node.children[i]);
    }
  }
  return result;
};

4. 实际应用

实际应用肯定不止我遇到的这一个，举例的话就以我自己的经历为例子了。

需求如下：

可以创建组织层级，大层级下有小层级，可以无限创建下去。同时，编辑的时候要将父层级全部列出来（iview 的 tree 以及 cascader 组件）。

简单来说就是从树中找到某个节点，并返回节点的路径。

4.1 深度优先搜索

算法：

1. 首先将根节点放入栈中（示例中没有根节点，直接将平行节点置入）；
2. 从栈中取出第一个节点，存储并检验是否为目标；
   • 如果找到目标，则返回存储路径；
   • 否则将当前节点的直接子节点推入栈中；
3. 重复步骤2；
4. 如果不存在未搜索的直接子节点，弹出存储节点中的最后一个节点
   • 如果存储的节点为空，判断栈中是否还有其他节点，重复步骤2
   • 否则结束搜索，报告结果
5. 获取存储节点当中最后一个节点，弹出第一个直接子节点；
6. 如果移除后的当前最后节点还存在直接子节点，重复步骤2（使用当前节点的第一个直接子节点）；
7. 重复步骤2（使用当前节点）；

// 深度优先搜索
const findPathByDepthFirstSearch = source => {
  const stack = JSON.parse(JSON.stringify(source));
  const result = [];
  const dfs = data => {
    // 保存当前节点
    // （在路口洒下面包屑）
    result.push(data);
    // 当前节点的值为真，则返回路径
    //（如果这个路口的终点是生门，通过记录的面包屑就找到了路径）
    if (data.id === target) {
      return result.map(r => r.id);
    }
    // 如果当前节点有子节点，则继续查找子节点
    //（如果这个路口后面还有分叉路口，就先去第一个分叉路口下的第一条路）
    if (data.children && data.children.length > 0) {
      return dfs(data.children[0]);
    }
    // 最后一个节点的值为假，弹出路径中的该节点
    //（最后一个路口是死路，清理最后一个路口的面包屑）
    result.pop();
    // 如果路径数组为空，则判断源节点是否还有待搜索的节点
    //（如果面包屑都清空了，也就是回到了原点，那就看看还有没有别的路口）
    if (result.length === 0) {
      return stack.length > 0 ? dfs(stack.shift()) : result;
    }
    // 获取路径中最后一个节点，是当前节点的父节点
    //（去撒有面包屑的最后一个路口看看，当前路口的面包屑已经在上面被清理了）
    const lastNode = result[result.length - 1];
    // 弹出路径中最后节点中的第一个子节点（前面已经查找失败了）
    //（当前路子不够野【在上面已经试过这条路，是死路】）
    lastNode.children.shift();
    // 查找最后一个有效节点的下一个子节点（前一个被 shift 了）
    //（如果这个路口下还有其他没尝试过的路，从第一条（实际是下一条了）开始尝试）
    if (lastNode.children.length > 0) {
      return dfs(lastNode.children[0]);
    }
    // 最后节点下的子节点全部尝试查找失败，返回上一个节点查找
    //（这个路口如果没有其他路了，清理面包屑且去上一个路口的第二条路看看【本条是第一条路，已经走过了】）
    return dfs(result.pop());
  };
  // 开始找路
  return dfs(stack.shift());
};

4.2 广度优先搜索

算法：

1. 首先将根节点放入队列（示例中没有根节点，直接将平行节点置入）；
2. 从队列中取第一个节点，并检验是否为目标；
   • 如果找到目标，结束搜索并递归查找 parent 存储，返回路径
   • 否则将它所有未检验过的直接子节点（需要路径结果，给直接子节点设置标志 parent）加入到队列
3. 若队列为空，表示所有节点都已经搜索过且无目标，结束搜索回传空；
4. 重复步骤二；

代码如下：

// 广度优先搜索
const findPathByBreadthFirstSearch = source => {
  let result = [];
  let queue = JSON.parse(JSON.stringify(source));
  while (queue.length > 0) {
    // 遍历队列（队列会动态增加）
    //（从第一个路口开始试探）
    for (let i = 0; i < queue.length; i += 1) {
      // 获取当前队列的一项
      // （这是一个路口）
      const node = queue[i];
      // 判断节点是否为目标节点
      //（路口是不是生门？）
      if (node.id === target) {
        // 队列清空
        //（已经找到生门，不用再接着找了）
        queue = [];
        // 通过 parent 一层层查找路径
        //（从这个路口通过面包屑【parent】找归途，直到找到回家的路）
        return (function findParent(data) {
          result.unshift(data.id);
          if (data.parent) {
            return findParent(data.parent);
          }
          return result;
        })(node);
      }
      // 节点有子节点，设置子节点的 parent 为当前节点，推入队列
      //（这个路口下还有其他路，先记住这个这个路口下的路是属于现在这个路口的【parent】
      // 然后去下一个路口，按顺序来试）
      if (node.children && node.children.length > 0) {
        queue.push(
          ...node.children.map(leaf => {
            leaf.parent = node;
            return leaf;
          })
        );
      }
    }
  }
  return result;
};

总结

一般来说，能用深度优先搜索的场景也能用广度优先搜索，从大脑的思考方式来说，深度优先搜索更符合人们的认知行为。与此同时，当节点足够复杂，可以考虑使用迭代深化深度优先搜索（重复运行一个有深度限制的深度优先搜索），时间复杂度与广度优先搜索一致，而空间复杂度远优。