深入理解hashmap（三）哈希表和二叉搜索树的恩怨情仇

前面两篇文章介绍了hashmap的源码和理论，今天把剩余的部分红黑树讲一下。理解好红黑树，对我们后续对hashmap或者其他数据结构的理解都是很有好处的。比方说为什么后面jdk要把hashmap中的单链表更新成红黑树？

要理解红黑树首先要弄清楚普通二叉树的一些基本概念

父节点和子节点，这个我就不多说了。应该都知道。

如果某几个子节点的父节点都是一个节点，那他们就是兄弟节点。

如果某个节点没有父节点，那他就是根节点。

如果某个节点没有子节点，拿他就是叶子节点

看下面这个二叉树：

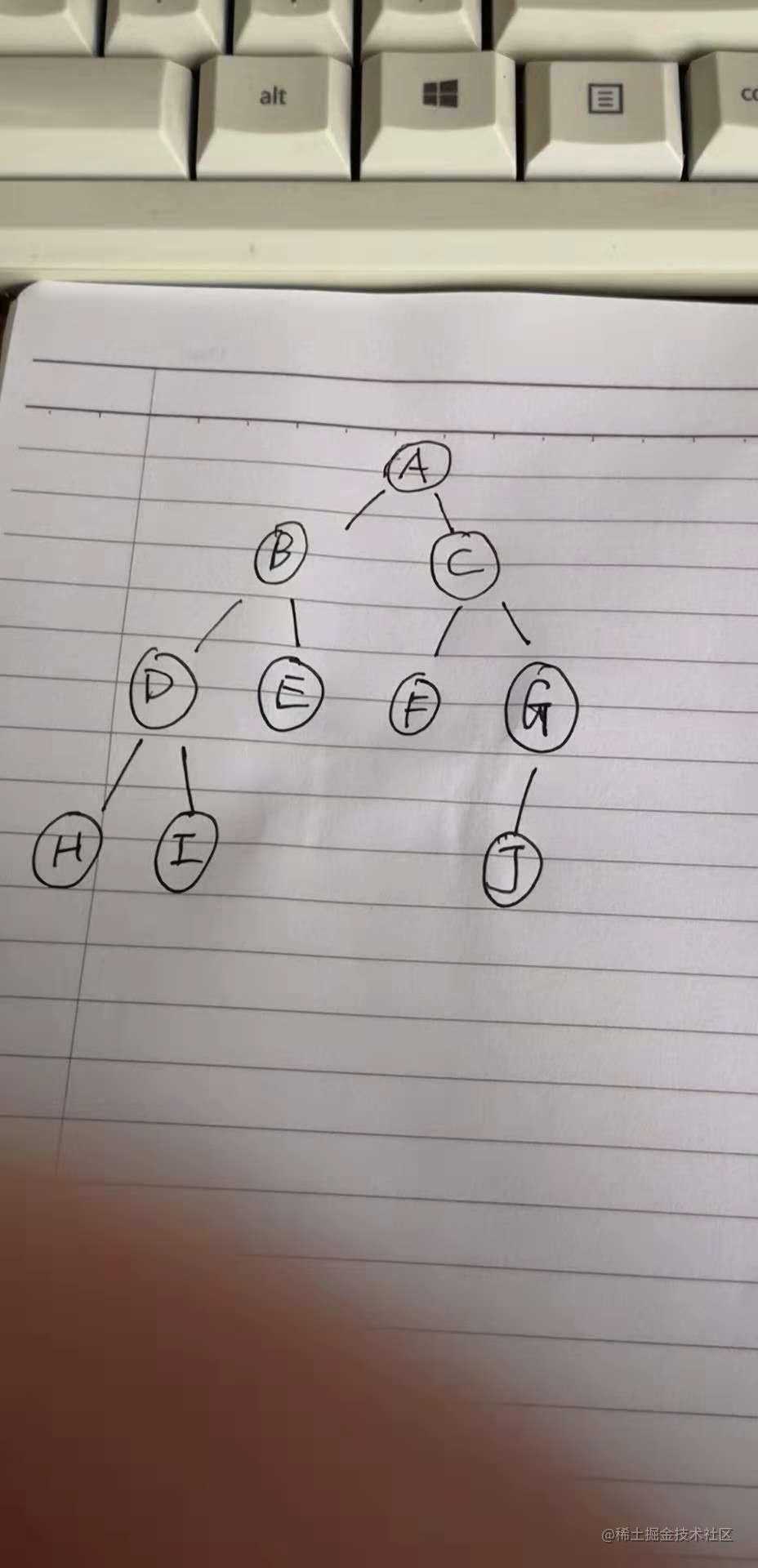
A节点的高度：就是节点A到最远端的叶子节点的边数。 比方说这里A节点的高度就是3

E节点的深度：就是根节点A到节点E的边数，这里明显就是2了，所以E节点的深度就是2

E 节点的层数：就是E节点的深度+1. 所以这里E节点的层数就是3.

再看这张图：

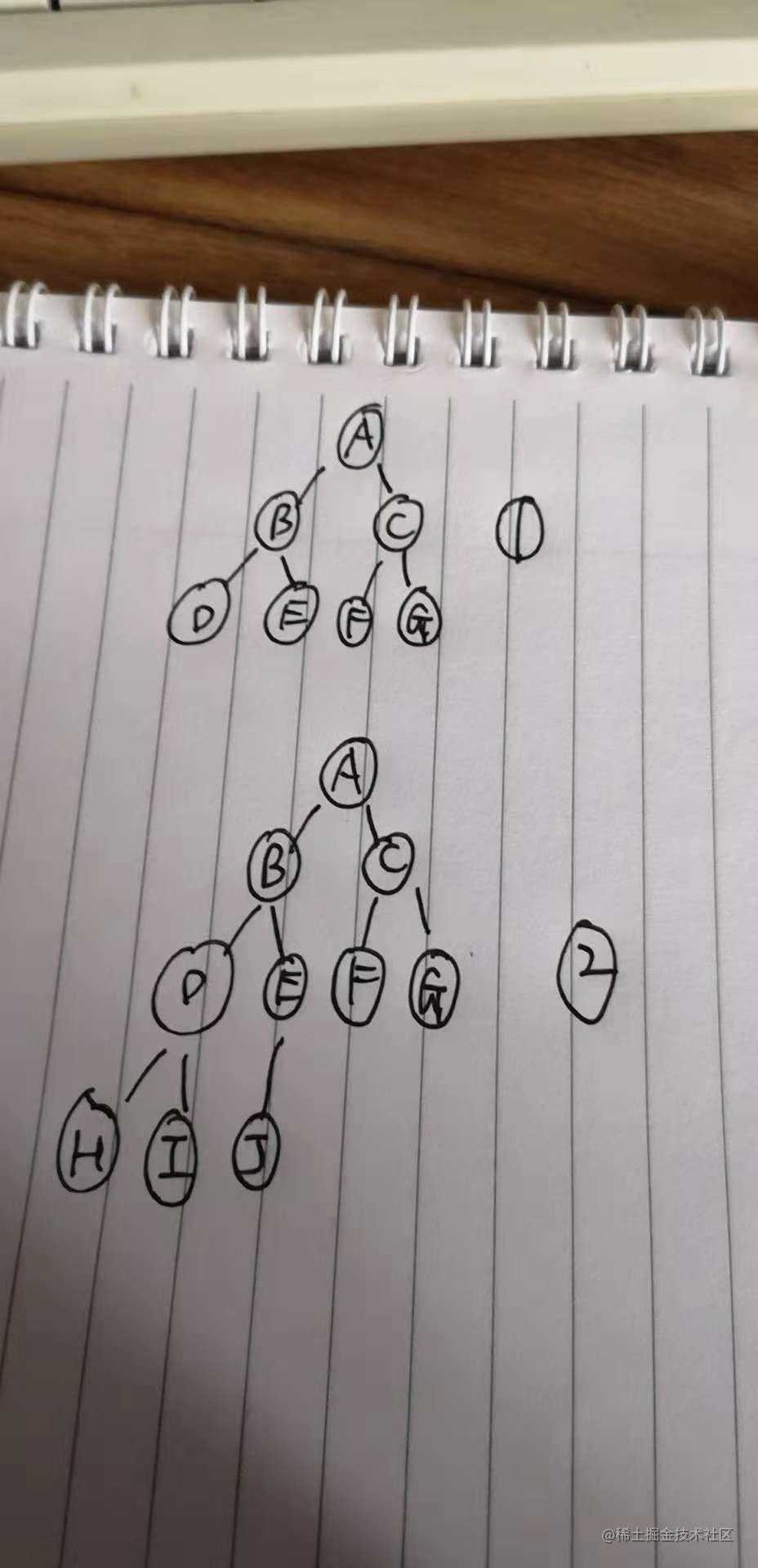
图1 就叫做满二叉树：

条件1：叶子节点全部在最下面

条件2：除了叶子节点以外，每个节点都有左右2个子节点。

满二叉树很好理解对吧，不多说了。我们继续看图2，

图2 就叫做 完全二叉树：

条件1：叶子节点只能在最下面2层。

条件2：最后一层的叶子节点都靠左排列。

条件3：除了最后一层，其他层的子节点个数必须达到最大。（也可以理解成：把最后一层去掉以后，必须是一个满二叉树）

恩，好像完全二叉树的判定就有点复杂了，没关系，我们看几个图练习一下

再看几张图：

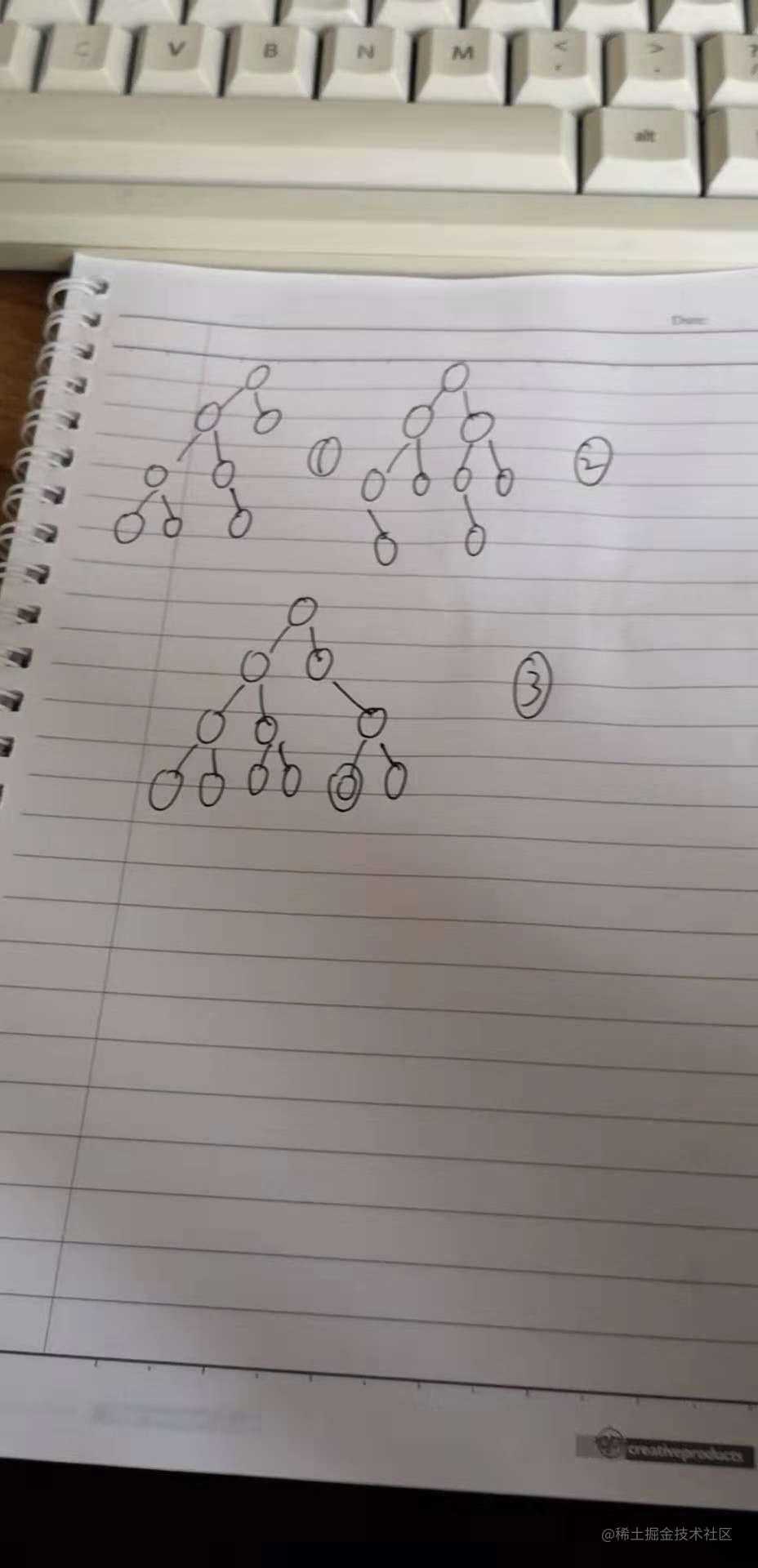
图1：不是完全二叉树吧，条件1就不符合。因为第二层就有一个叶子节点了

图2：不符合条件2，图2 里最后一层叶子节点都向右边了

图3：不符合条件3 ，因为我们把最后一层去掉以后发现并不是一个满二叉树。

为什么要有一个完全二叉树，这东西干啥的？为什么条件2要求最后一层叶子节点都靠左排列？向右不可以吗？

首先要明确一个概念，二叉树除了用链表实现以外，还可以用数组来实现。

链表实现的二叉树不多说了，网上太多了，其实数据结构就是一个data字段，然后配一个left指针和right指针。

那如果用数组来做，怎么存储一个二叉树呢？看下面这张图：

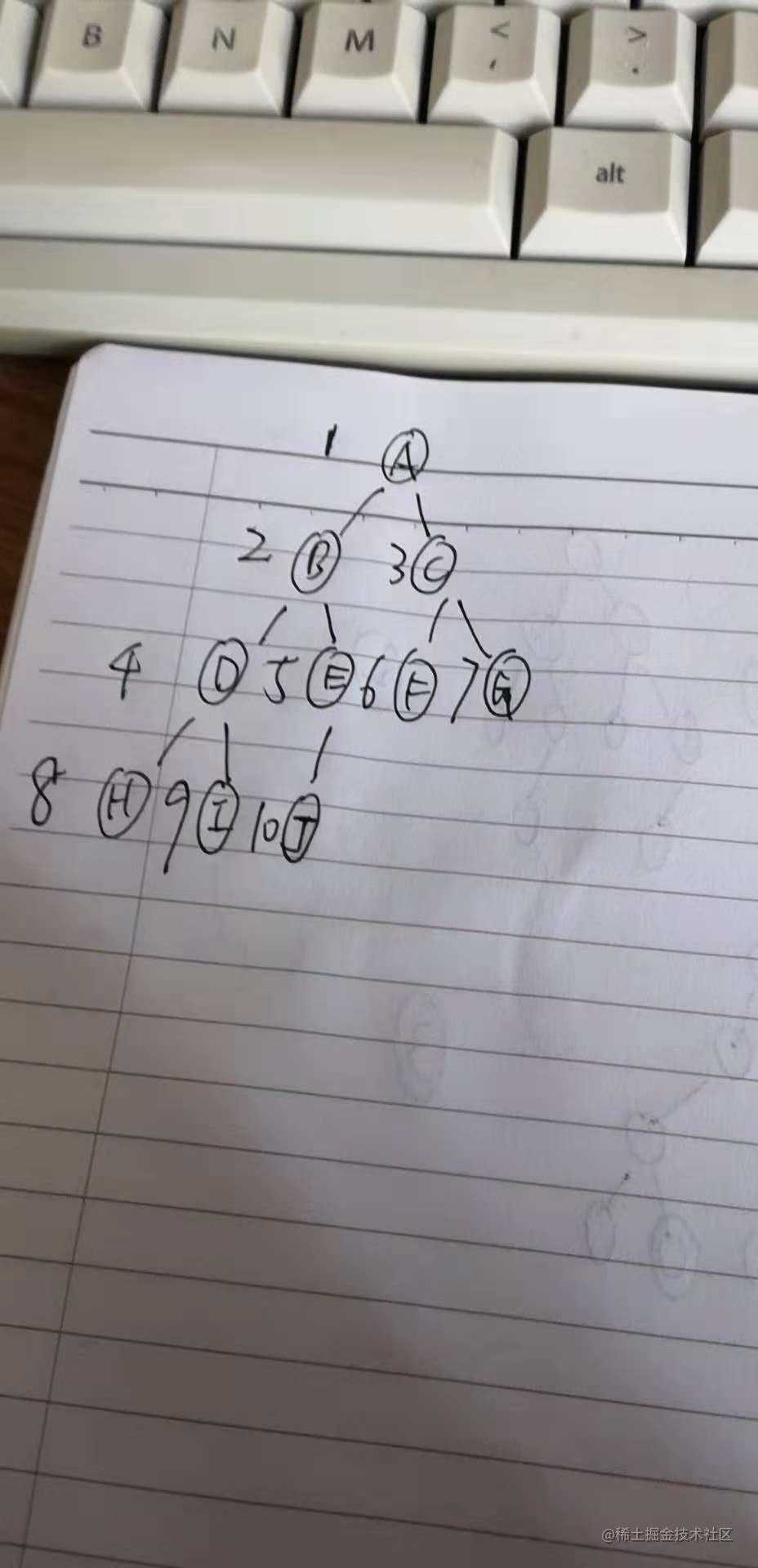
很好理解吧，数字就代表数组的下标。比如说 跟节点A 就放在[1]位置，节点F 就放在[6]位置，节点I就放在[9]位置，等等

所以数学归纳法以后，我们可以抽象出如下的规则：

如果一个二叉树用数组来存储，那么节点对应的下表规则如下：

规则1：下标为2*i的 必然是左子节点。

规则2：下标为2*i+1 的，必然是右子节点。

规则3：下标为i/2的节点必然是 节点i的 父亲节点。

所以我们只要把一个二叉树的根节点放到数组的任意一个位置中，就必然可以把整个二叉树利用上述的规则串联起来，整个就是二叉树的数组存储法。

而用数组存储二叉树的好处就是可以节省left和right 这2个指针，可以节约内存空间

再看一张图：

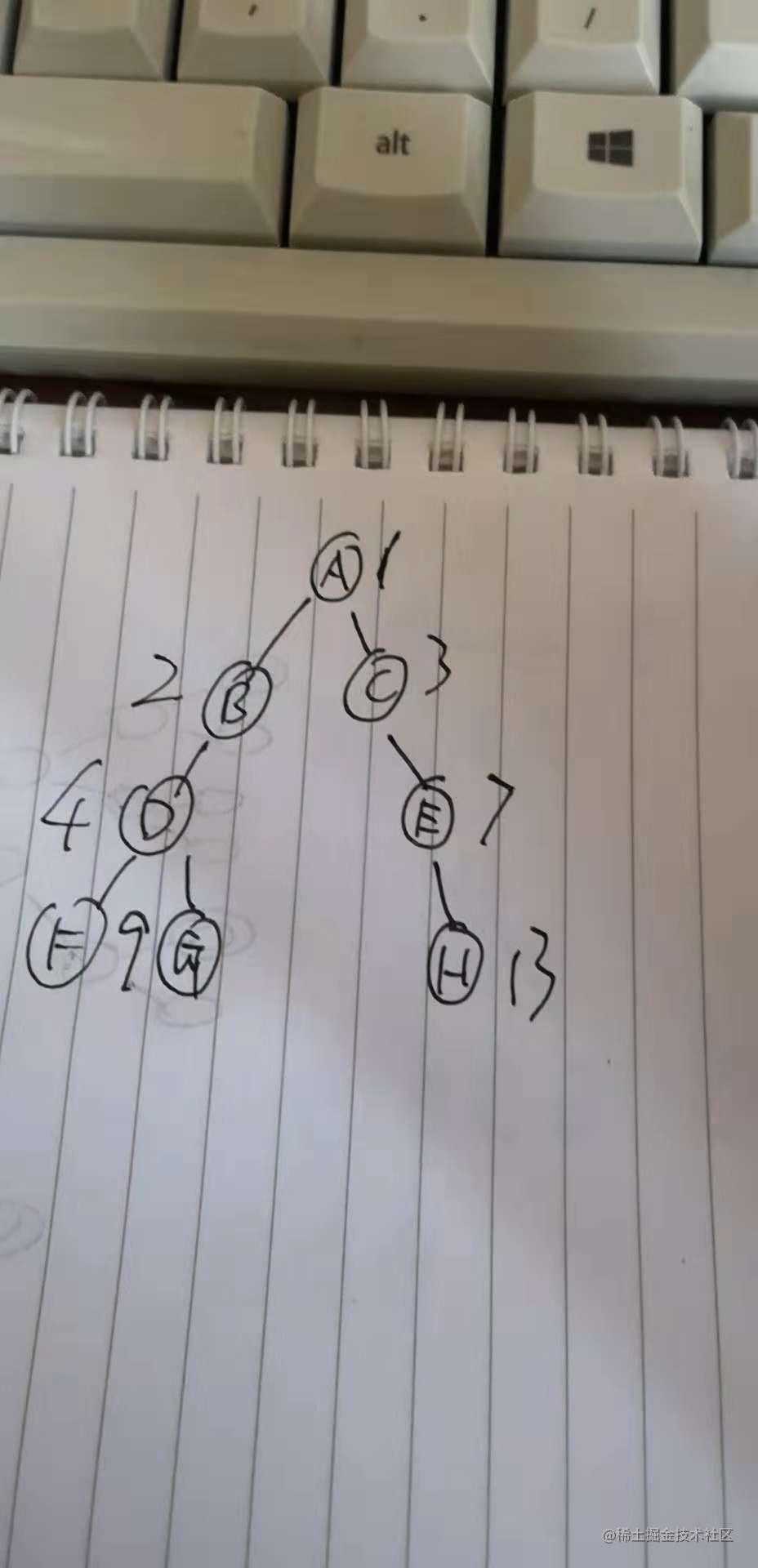
你看这个二叉树，我们的出来的数组下标是 1，2，3，4，7，8，9，13.

浪费了 5，6，10，11，12. 浪费了这5个数组空间空闲在那里。

所以完全二叉树的优点就是不会浪费任何数组空间，所以对于完全二叉树来说，数组存储是最合适的方法，比方说堆就是用数组来 做二叉树的存储结构的

前序遍历：先打印节点本身，再打印左子树，再打印右子树

中序遍历：左子树-节点本身-右子树

后序遍历：左子树-右子树-节点本身

那这三种遍历的方法我就不多说了，网上一搜一大堆。

有了这些前置的概念 我们就可以继续深挖。

二叉搜索树是咩啊？

二叉搜索树：对于任意一个节点来说，他的左节点的值都要小于这个节点，右节点的值都要大于这个节点。

那么，我们来对一个二叉搜索树进行他的 查找，插入操作。 为什么要学这个，因为对于大部分数据结构来说，衡量他的

性能主要就是 看查找数据和插入数据的效率。比方说数组和链表 就是查找和插入效率截然相反的两种数据结构。

废话不多说，我们首先来看一下二叉搜索树的 查找操作要怎么完成：

其实也很简单，对于二叉搜索树来说， 左节点的值《父节点《右节点。

所以想查找一个值，我们只要从二叉搜索树的顶部也就是根节点来遍历即可：

如果这个值比节点大，那么就去右子树继续递归查找，如果这个值比节点的值小，那么就去左子树查。直到找到为止

这个递归函数我就不写了，大家知道这个算法思路就可以，自己多练习一下。

二叉搜索树的插入操作就稍微复杂一点：

1.如果要插入的值，比节点的值要大，并且这个节点的右子树为空，那么就直接放在这个节点的右节点位置上（注意哦，这个就是递归的结束条件）

2.如果不为空，那么就继续 步骤1的操作，直到我们找到对应的节点位置为止。

3. 如果插入的值 比节点的值要小，并且这个节点的左子树为空，那么就直接放在节点的左节点位置上。。 以此类推。和步骤1-2 其实是一个思路

可以看出来，递归是实现二叉树相关算法的核心思想。

此外最重要的一点，我们再回顾一下这个二叉搜索树的特性你会发现：如果我们用中序遍历的方法 print这个 二叉搜索树，那么 得到的结果一定是一个有序的。时间复杂度为o(n)

所以，二叉搜索树又叫二叉排序树。

如果二叉搜索树中有重复的数据要插入怎么办？

这个问题问的好，这里给出2个解决方案，大家有兴趣可以实现一下

方案1：

正常情况下，我们一个二叉树如果用链表来实现，那么基础数据结构肯定是 data字段和left以及right指针对吧，那么

我们可以人为的增加一个字段，叫 more指针。这个指针是干嘛的呢？这个指针就是把重复的数据串起来。

比方说下图的例子：

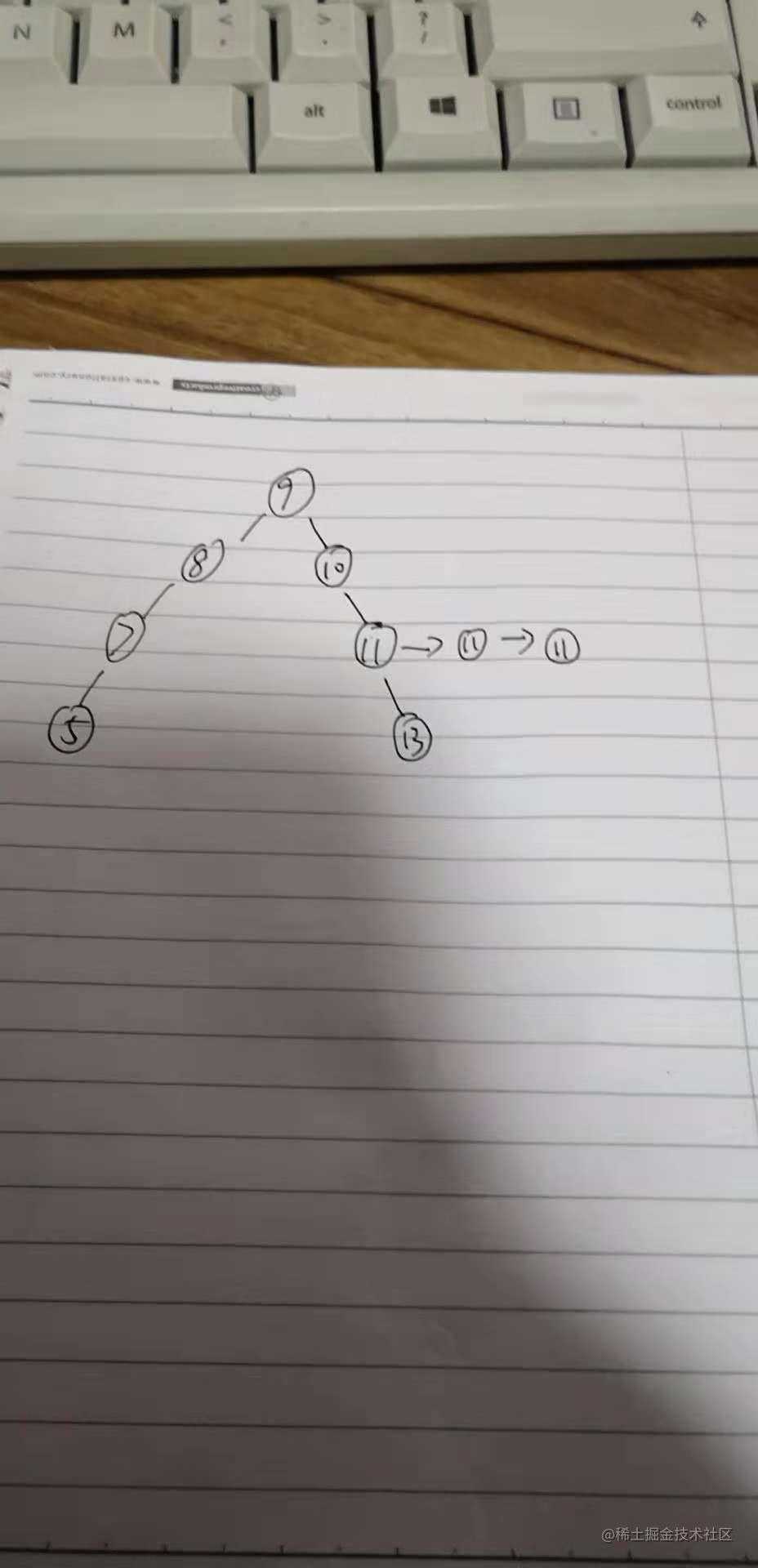
大家可以看一下，这个二叉搜索树的 11的那个节点 有一个链表，存储的都是值为11的节点。

这个处理方式是不是有点像hashmap中处理哈希冲突的方法？

那有人又要问了，重复的值插到二叉搜索树的意义何在？

在实际生产中，我们存储的数据结构不可能是一个个简单的int值，而是一个个对象，那么一个个对象里面肯定有很多字段， 比如 商品这个对象，可以有很多字段，价格，商品名称，商品图片等。 如果用商品价格来作为二叉搜索树的key值， 那么就肯定会出现这种情况,因为相同价格的商品可以是不同的商品，比如iphone和mate20 都卖7000元，但显然他们是不 一样的东西

方案2：

在插入数据的时候，如果发现插入的值和节点的值相同，那么就把这个值插入到这个节点的右节点的位置。（也就是说 插入一个大于节点的值和插入一个等于节点的值 方法是一样的）

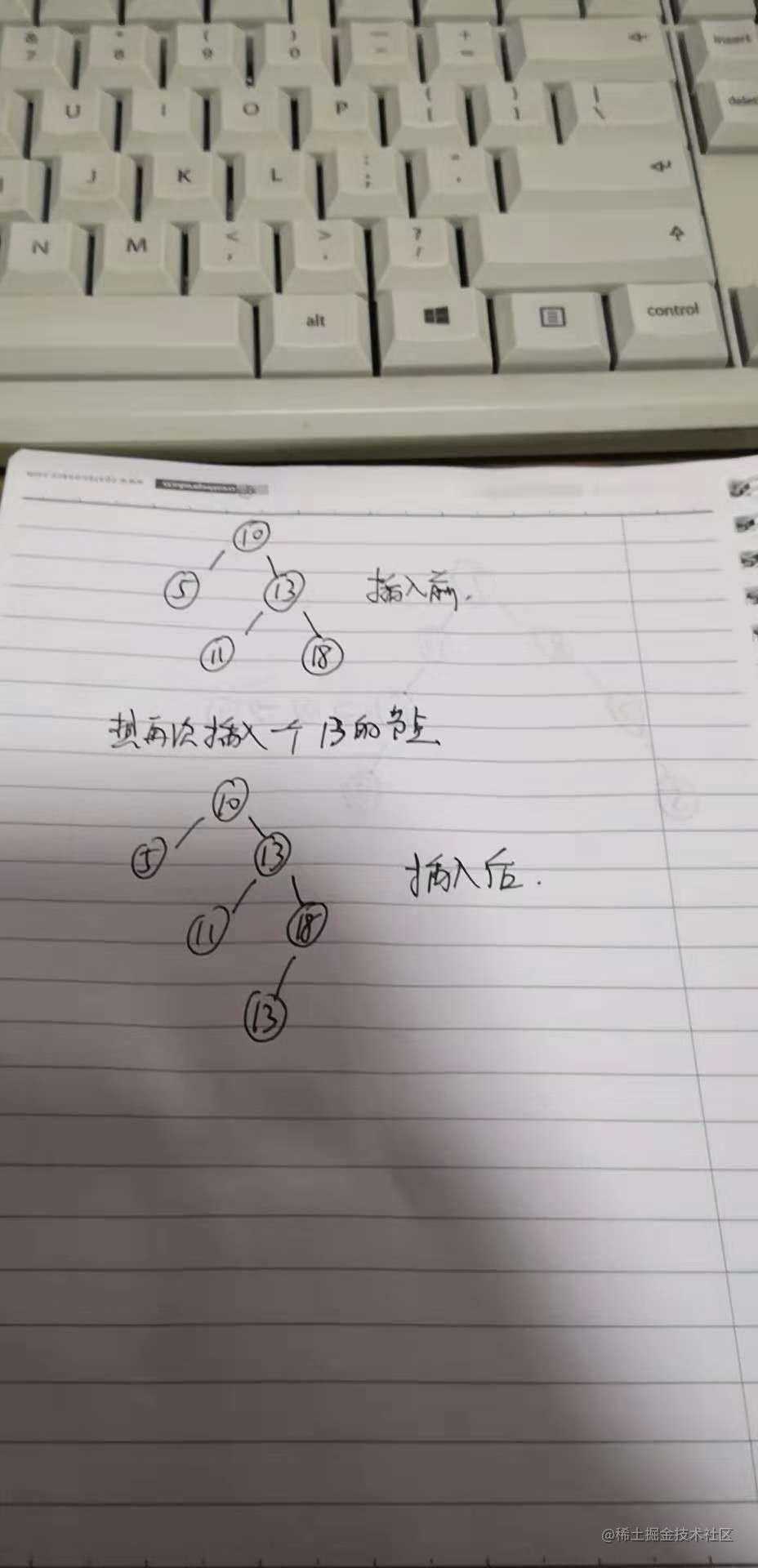
那么针对这种情况，我们的查找方法就要修改一下了，不能说是找到和节点相同的值就退出递归了，而是找到相同节点的值以后 还要继续找他的右子树，看看有没有值和查找的值相同，一直到叶子节点为止（注意退出递归的条件）

二叉搜索树的效率如何？看起来不如哈希表啊，存在的意义何在？

实际上，我们看一下二叉搜索树的算法可以得出来一个结果，他的查找效率是O(logn)的，完全不如哈希表查找的效率o(1). 且，二叉搜索树极端情况下很容易退化成单链表，那么单链表的查找效率我们都知道是O(N)的。这个就更慢了。

但，即便如此，二叉搜索树还有一些哈希表不具备的优点：

1. 二叉搜索树用中序遍历可以很容易对 数据进行排序，这个是哈希表做不到的。

2. 哈希表遇到哈希冲突的时候需要扩容，这个扩容操作相当耗时，性能有时候不稳定，虽然说二叉搜索树的性能也不稳定， 但是 我们有更特殊的 平衡二叉搜索树可以把时间复杂度稳定在O(logn)

3. 二叉搜索树比较简单，数据结构一目了然，递归递归递归就行了，但是哈希表你们懂的，实现起来超级复杂。

所以可以知道，hashmap和二叉搜索树各有各的优点，具体怎么用，还是要看实际情况，但是大家要知道这两种数据结构的 优劣在哪里以及为什么？

千呼万唤始出来的 红黑树到底是什么？和我们上面提到的平衡二叉搜索树又是什么关系呢？

前面我们说到了，普通的二叉搜索树极端情况下会退化成单链表，比如说：

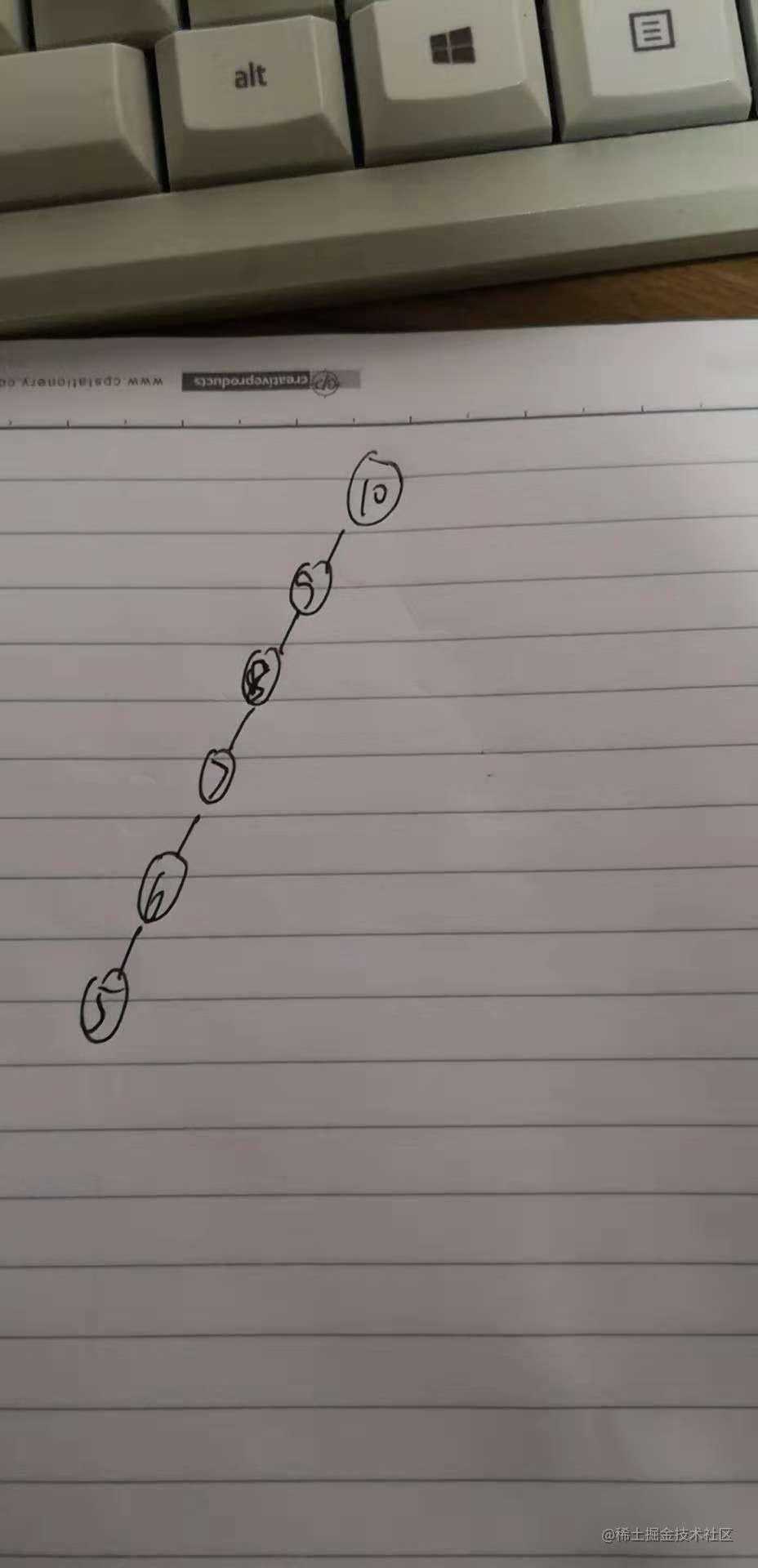
你看这个二叉搜索树运气就非常差，全在左边，一点都不平衡，看起来跟个单链表一样，一看就是很慢的数据结构。

所以 所谓的平衡二叉搜索树就是要想办法保证在插入的过程中，让这个二叉搜索树变的平衡起来，所谓的平衡起来 就是不能全在左边或者全在右边，最好是左右两边都有，且左右两边子树的高度越接近就越好就越平衡。因为只有这样 我们的时间复杂度才会稳定在 O(logn)

平衡二叉搜索树的实现方法有很多，其中最出名的就是红黑树了，对于我们普通写业务代码不是专业写算法的人来说 红黑树几乎就可以代表平衡二叉搜索树，两者无限接近。

但是我们要注意的是，红黑树是近似平衡的 平衡二叉搜索树，并不是严格的平衡二叉树，有兴趣的同学可以查一查AVL树 这个才是严格平衡二叉树，不过这个东西因为太严格导致每次插入删除的效率太低，所以生产环境用的人很少。

关于红黑树的具体实现，我这里就不多说了，因为红黑树的实现比较复杂，我估计除非是写算法的人，否则绝大多数人 一辈子都不会写一次红黑树，如果实在要用，实际上跳表写起来比红黑树简单多了。。也好理解。

所以这里有兴趣的同学可以自行搜索红黑树的相关资料，开开眼界。没有兴趣的同学就只要知道红黑树是一种平衡二叉查找树，它是为了解决普通二叉查找树在数据插入的时候容易退化成单链表导致效率大幅降低的数据结构。他的高度会无限接近于log2n，所以 他的查找效率也就可以稳定在O(logn)了。这也就是为什么hashmap在高版本jdk中的实现 用红黑树代替单链表来解决哈希碰撞的原因。