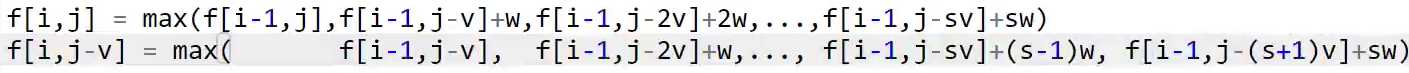背包九讲

概述

本文参考自bilibili上up主大雪菜的背包九讲专题：背包九讲专题1、背包九讲专题2 以及AcWing上的相关讲解。

背包问题代表了一类问题，即组合类的最优化问题，就是如果给我们一堆物品（元素），我们要按照某种限从中选出若干个物品（元素），求最大/最小值。

本文将将对如下的九种背包问题给出分析过程以及实现代码（提供C++和Java代码，代码链接：github），最后还给出了Leetcode上部分相关的背包问题以及解答。

/*
1. 01背包问题
2. 完全背包问题
3. 多重背包问题
4. 混合背包问题
5. 二维费用背包问题
6. 分组背包问题
7. 背包问题求方案数
8. 求背包问题的方案
9. 有依赖的背包问题
*/

背包问题是一类典型的动态规划问题，一般对于动态规划问题，常规分析方式是给出状态定义和状态转移，这里为了更加容易理解，采用yxc提出的闫式dp分析法。

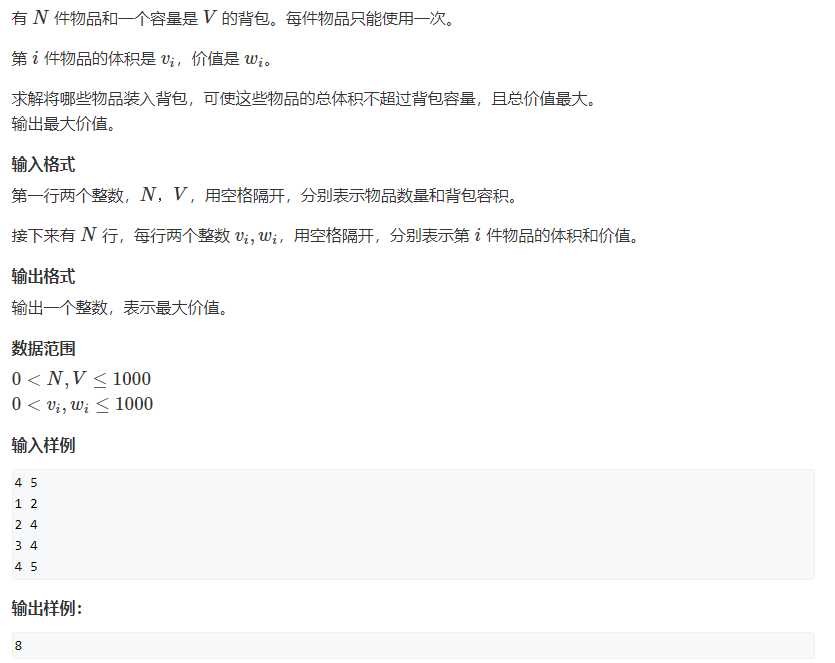
一. 01背包问题

问题描述

问题链接：01背包问题

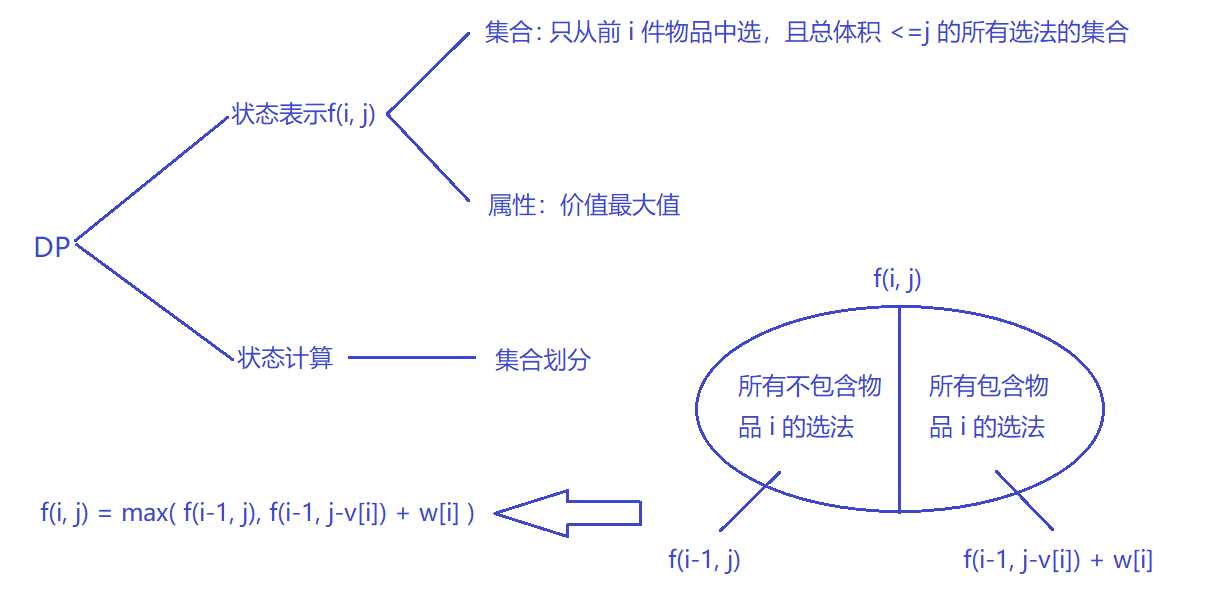
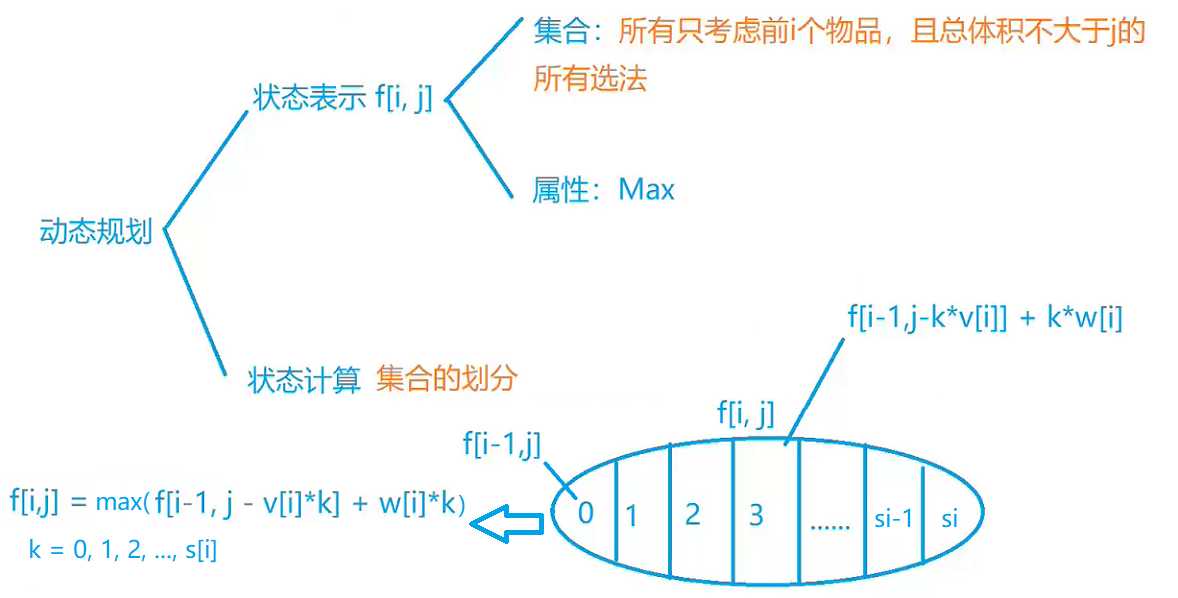
分析

代码

C++：

// Created by WXX on 2021/2/24 13:46
#include <iostream>

using namespace std;

const int N = 1010;  // 多开几个数据，防止数组下标越界

int n, m;  // 物品种类数，背包容积
int v[N], w[N];  // 体积，价值。注意：v[1]存储第一件物品，索引0未使用
int f[N][N];  // dp数组

int main() { 
   
    // 读入数据
    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    // 算法过程，因为f[0][0~m]初始就为0，因此初始化可以省略
    for (int i = 1; i <= n; i++) { 
     // 先循环物品
        for (int j = 0; j <= m; j++) { 
     // 再循环容量
            // 最后循环决策
            f[i][j] = f[i - 1][j];  // 不选第i件物品
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);  // 考虑选第i件物品
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

Java

import java.util.Scanner;

// Created by WXX on 2021/2/24 14:15
public class Main { 
   

    public static final int N = 1010;  // 多开几个数据，防止数组下标越界

    static int n, m;  // 物品种类数，背包容积
    static int[] v = new int[N], w = new int[N];  // 体积，价值。注意：v[1]存储第一件物品，索引0未使用
    static int[][] f = new int[N][N];   // dp数组

    public static void main(String[] args) { 
   
        // 读入数据
        Scanner sn = new Scanner(System.in);
        n = sn.nextInt(); m = sn.nextInt();
        for (int i = 1; i <= n; i++) { 
   
            v[i] = sn.nextInt(); w[i] = sn.nextInt();
        }

        // 算法过程，因为f[0][0~m]初始就为0，因此初始化可以省略
        for (int i = 1; i <= n; i++) { 
     // 先循环物品
            for (int j = 0; j <= m; j++) { 
     // 再循环容量
                // 最后循环决策
                f[i][j] = f[i - 1][j];  // 不选第i件物品
                if (j >= v[i]) f[i][j] = Math.max(f[i][j], f[i - 1][j - v[i]] + w[i]);  // 考虑选第i件物品
            }
        }
        System.out.println(f[n][m]);
    }
}

代码优化（只用C++演示）

考虑到在计算 f 的时候，当计算第 i 行时，只用到了第 i – 1 行的数据，因此可以用滚动数组优化

// Created by WXX on 2021/2/24 14:29
#include <iostream>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[2][N];

int main() { 
   

    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++) { 
   
        for (int j = 0; j <= m; j++) { 
   
            f[i & 1][j] = f[(i - 1) & 1][j];
            if (j >= v[i]) f[i & 1][j] = max(f[i & 1][j], f[(i - 1) & 1][j - v[i]] + w[i]);
        }
    }
    cout << f[n & 1][m] << endl;
    return 0;
}

其实这里还可以将 f 数组优化为一维数组，但是考虑到要用到上一行数据，因此第二层循环应该从大到小进行遍历，这样每次更新用到的就是未被更新的数据

// Created by WXX on 2021/2/24 14:36
#include <iostream>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main() { 
   

    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++)
        for (int j = m; j >= v[i]; j--)
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;
    return 0;
}

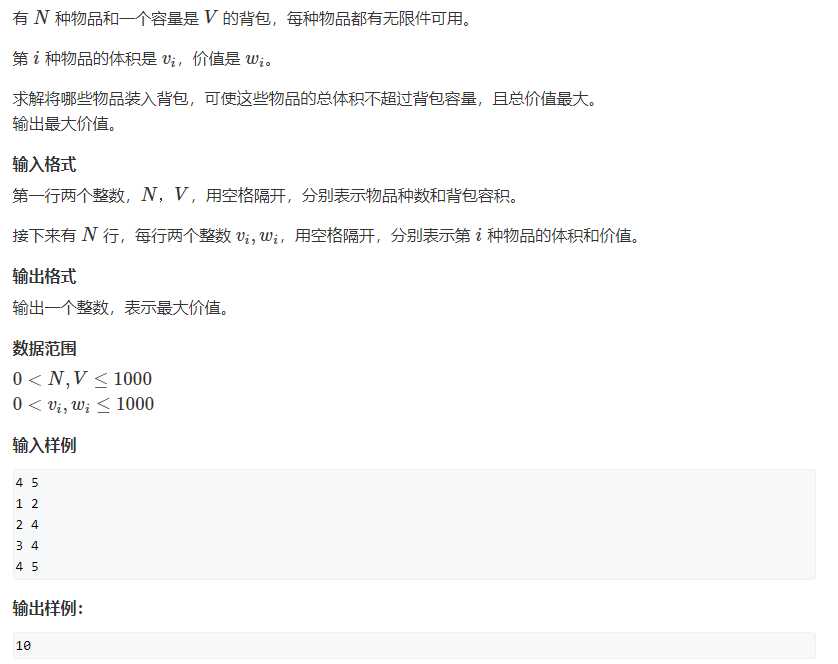
二. 完全背包问题

问题描述

问题链接：完全背包问题

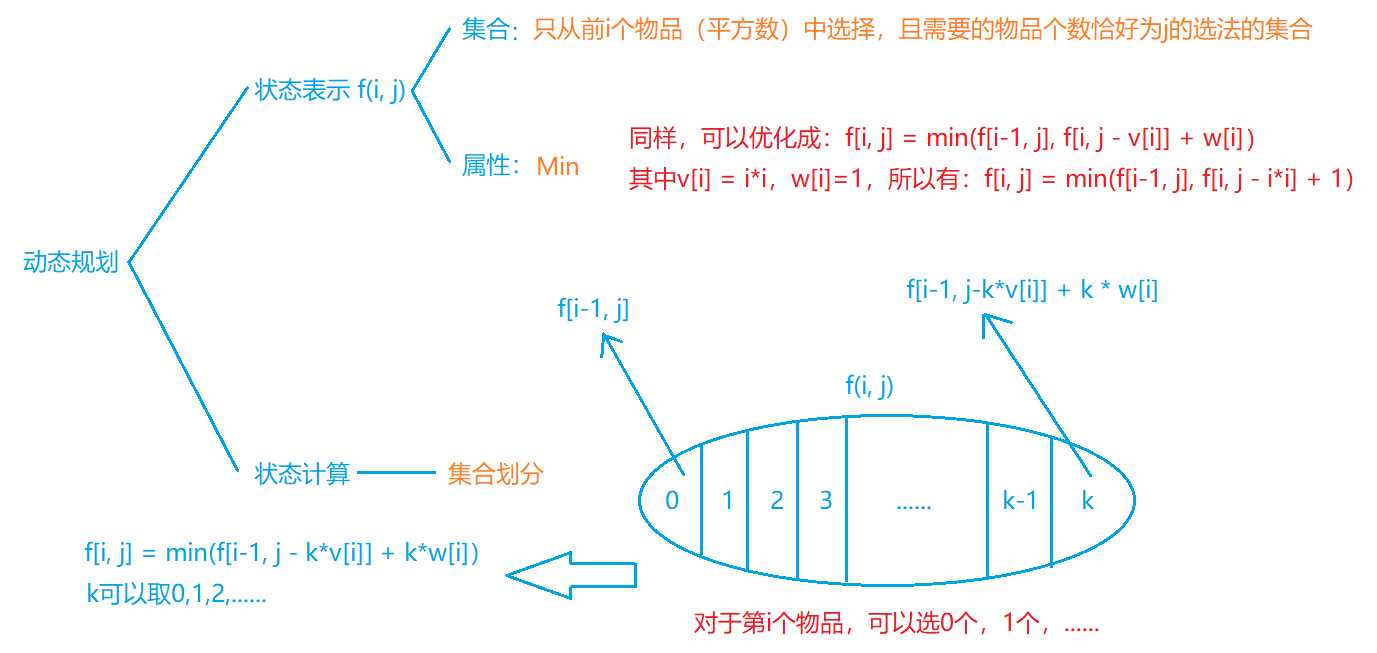
分析

代码

C++：

// Created by WXX on 2021/2/24 14:52
#include <iostream>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

// TLE
int main() { 
   

    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++)  // 先循环物品
        for (int j = 0; j <= m; j++)  // 再循环容量
            for (int k = 0; k * v[i] <= j; k++)  // 最后循环决策
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
    cout << f[n][m] << endl;
    return 0;
}

Java：

import java.util.Scanner;

// Created by WXX on 2021/2/24 14:58
public class Main { 
   

    public static final int N = 1010;

    static int n, m;
    static int[] v = new int[N], w = new int[N];
    static int[][] f = new int[N][N];

    public static void main(String[] args) { 
   

        Scanner sn = new Scanner(System.in);
        n = sn.nextInt(); m = sn.nextInt();
        for (int i = 1; i <= n; i++) { 
   
            v[i] = sn.nextInt(); w[i] = sn.nextInt();
        }

        for (int i = 1; i <= n; i++)  // 先循环物品
            for (int j = 0; j <= m; j++)  // 再循环容量
                for (int k = 0; k * v[i] <= j; k++)  // 最后循环决策
                    f[i][j] = Math.max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
        System.out.println(f[n][m]);
    }
}

代码优化（只用C++演示）

我们可以将 $f (i, j) = f (i - 1, j - k * v [i]) + k * w [i]$ 展开，就可以发现如下规律：

因此代码可以根据 $f (i, j) = m a x (f (i - 1, j), f (i, j - v) + w)$ 进行优化：

// Created by WXX on 2021/2/24 15:21
#include <iostream>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main() { 
   

    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++)
        for (int j = 0; j <= m; j++) { 
   
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
        }
    cout << f[n][m] << endl;
    return 0;
}

这里还可以将 f 数组优化为一维数组，因为不需要用到上一行数据，要用到本行之前计算出来的户籍，因此第二层循环应该从小到大进行遍历

// Created by WXX on 2021/2/24 15:21
#include <iostream>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N];

int main() { 
   

    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i++)
        for (int j = v[i]; j <= m; j++)
            f[j] = max(f[j], f[j - v[i]] + w[i]);
    cout << f[m] << endl;
    return 0;
}

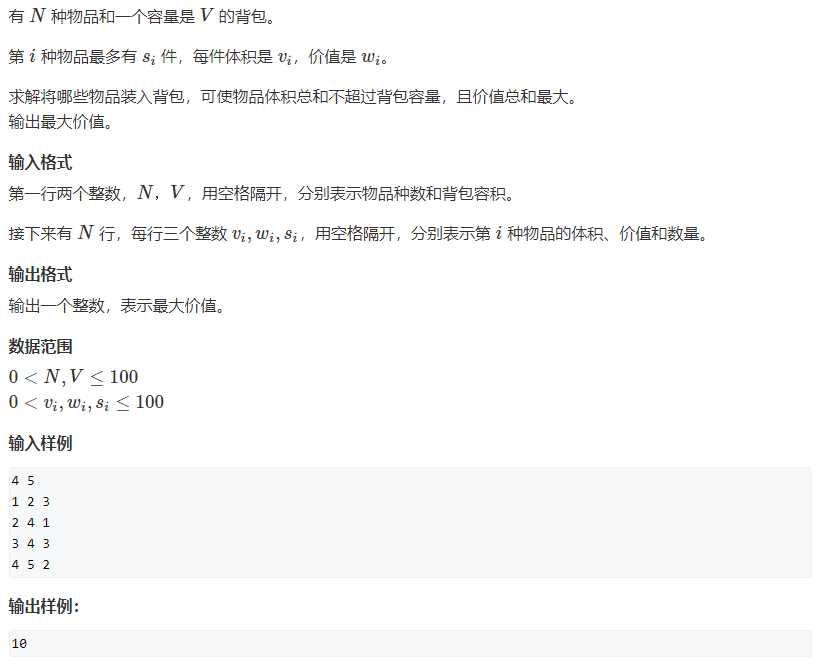
三. 多重背包问题

3.1 多重背包问题 I

问题描述

问题链接：多重背包问题 I

分析

代码

// Created by WXX on 2021/2/24 16:07
#include <iostream>

using namespace std;

const int N = 110;

int n, m;
int v[N], w[N], s[N];
int f[N][N];

int main() { 
   

    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i] >> s[i];

    for (int i = 1; i <= n; i++)  // 先循环物品
        for (int j = 0; j <= m; j++)  // 再循环容量
            for (int k = 0; k <= s[i] && k * v[i] <= j; k++)  // 最后循环决策
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
    cout << f[n][m] << endl;
    return 0;
}

Java

import java.util.Scanner;

// Created by WXX on 2021/2/24 16:13
public class Main { 
   

    public static final int N = 110;

    static int n, m;
    static int[] v = new int[N], w = new int[N], s = new int[N];
    static int[][] f = new int[N][N];

    public static void main(String[] args) { 
   

        Scanner sn = new Scanner(System.in);
        n = sn.nextInt(); m = sn.nextInt();
        for (int i = 1; i <= n; i++) { 
   
            v[i] = sn.nextInt(); w[i] = sn.nextInt(); s[i] = sn.nextInt();
        }

        for (int i = 1; i <= n; i++)  // 先循环物品
            for (int j = 0; j <= m; j++)  // 再循环容量
                for (int k = 0; k <= s[i] && k * v[i] <= j; k++)  // 最后循环决策
                    f[i][j] = Math.max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
        System.out.println(f[n][m]);
    }
}

3.2 多重背包问题 II

问题描述

问题链接：多重背包问题 II

分析

这一题不能使用类似于完全背包问题的方式进行优化，可以将 $f (i, j) = f (i - 1, j - k * v) + k * w, k = 0, 1, . . ., s$ 展开，如下：

我们发现 $f [i, j - v]$ 中比 $f [i, j]$ 最后多了一项，不能直接得到这两者的关系，所以不能使用类似于完全背包问题的方式进行优化。

本次的优化方式为二进制优化，将s件物品进行拆分，然后可以转化成01背包问题

/*
例如 s=10
10可以拆分为0、1、2、4、3；
前四个数可以凑出0~7之间的任何数据，加上3可以凑出3~10之间的任何数据，因此这5个数可以凑出0~10内的任何数据；
相当于将10个物品打包成4个物品，打包后的物品的体积和价值分别为单个物品的1、2、4、3倍；
这四个物品都是可选可不选，因此就转化成了01背包问题。

例如 s=200
200可以拆分为0、1、2、4、8、16、32、64、73；
一共8个物品

总结：对于s，可以划分为 log(s) 上取整个单一物品，然后用01背包问题的思路解决即可，时间复杂度：O(N*V*log(s))
*/

代码

// Created by WXX on 2021/2/24 16:42
#include <iostream>
#include <vector>

using namespace std;

const int N = 2010;

int n, m;
int f[N];

struct Good { 
   
    int v, w;
};

int main() { 
   

    vector<Good> goods;
    cin >> n >> m;
    for (int i = 0; i < n; i++) { 
   
        int v, w, s;
        cin >> v >> w >> s;
        for (int k = 1; k <= s; k *= 2) { 
   
            s -= k;
            goods.push_back({ 
   k * v, k * w});
        }
        if (s > 0) goods.push_back({ 
   s * v, s * w});
    }

    for (auto good : goods)
        for (int j = m; j >= good.v; j--)
            f[j] = max(f[j], f[j - good.v] + good.w);
    cout << f[m] << endl;
    return 0;
}

Java

import java.util.ArrayList;
import java.util.Scanner;

// Created by WXX on 2021/2/24 16:50
public class Main { 
   

    public static final int N = 2010;

    static int n, m;
    static int[] f = new int[N];

    static class Good { 
   
        int v, w;
        public Good(int v, int w) { 
   
            this.v = v;
            this.w = w;
        }
    }

    public static void main(String[] args) { 
   

        ArrayList<Good> goods = new ArrayList<>();
        Scanner sn = new Scanner(System.in);
        n = sn.nextInt(); m = sn.nextInt();
        for (int i = 0; i < n; i++) { 
   
            int v = sn.nextInt(), w = sn.nextInt(), s = sn.nextInt();
            for (int k = 1; k <= s; k *= 2) { 
   
                s -= k;
                goods.add(new Good(k * v, k * w));
            }
            if (s > 0) goods.add(new Good(s * v, s * w));
        }

        for (Good good : goods)
            for (int j = m; j >= good.v; j--)
                f[j] = Math.max(f[j], f[j - good.v] + good.w);
        System.out.println(f[m]);
    }
}

3.2 多重背包问题 III

问题描述

问题链接：多重背包问题 III

分析

DP分析和 3.1 多重背包问题 I 完全一致，但是本题的数据量更大，需要进一步优化，这里采用滑动窗口求最值的方式优化

还有一个问题需要解决，就是窗口每次向右滑动一格，除了滑出窗口外的元素，其余的元素在下一次比较中都需要加上一个偏移量w，这个问题可以通过如下方式解决（参考网址）：

/*
因为每次循环都只需要用到第i-1层的结果,所以在这里:
g:第i-1层结果
f:第i层结果

如果一共有3个物品，即s=3的话:
取r=1，那么f[3*v+1]的最大值为 f[3*v+1] = max(g[3*v+1], g[2*v+1]+w, g[v+1]+2w, g[1]+3w);


所以我们可以得到下列算式:(其中r表示余数)
f[r]=       g[r];
f[r+v]= max(g[r] + w,  g[r+v]);
f[r+2v]=max(g[r] + 2w, g[r+v] + w,  g[r+2v],);
f[r+3v]=max(g[r] + 3w, g[r+v] + 2w, g[r+2v] + w, g[r+3v]);
……
f[r+sv]=max(g[r] + sw,……, g[r+(s-1)v] + w, g[r+sv]);

可以发现上面的等式上下存在偏移量w,所以可以减去kw再加上kw进行转换
f[r]=       g[r];
f[r+v]= max(g[r], g[r+v] - w) + w;
f[r+2v]=max(g[r], g[r+v] - w, g[r+2v] - 2w) + 2w;
f[r+3v]=max(g[r], g[r+v] - w, g[r+2v] - 2w, g[r+3v] - 3w) + 3w;
……
f[r+sv]=max(g[r], ……, g[r+(s-1)v] - (s-1)w, g[r+sv] - sw) + sw;
每次单调队列q (q中存储的是体积，如r,r+v,...) 用队尾数据和要插入的数据进行比较时，需要减去一个数
这里比较的其实是上面max小括号中的数据
队尾数据：g[a] - (a-r)/v * w，其中a是队尾体积q[tt] ==> g[q[tt]] - (q[tt]-r)/v * w
即将滑入滑动窗口的数据：g[k] - (k-r)/v * w，其中k是当前考察的同余的体积，例如k=r+3v等

另外还要注意，f中真实存储的数据为：g[q[hh]] + (q[hh]-r)/v * w，其中(q[hh]-r)/v * w为当前考察物品的收益
*/

关于滑动窗口求最值，这是一个经典的问题，在LeetCode上有对应的问题：Leetcode 0239 滑动窗口最大值；在AcWing上也有对应的练习：AcWing 0154. 滑动窗口

这里给出 Leetcode 0239 滑动窗口最大值的C++解法（注意：这里的滑动窗口大小必须是k，不能小于k；多重背包中的滑动窗口为1，然后变为2，直到到达v后不再改变）：

// 考点：单调队列
/** * 执行用时：240 ms, 在所有 C++ 提交中击败了97.90%的用户 * 内存消耗：114.1 MB, 在所有 C++ 提交中击败了88.81%的用户 */
class Solution { 
     
public:
    vector<int> maxSlidingWindow(vector<int> &nums, int k) { 
     
        int n = nums.size();
        int q[n];
        int hh = 0, tt = -1;
        vector<int> res;
        for (int i = 0; i < nums.size(); i++) { 
     
            if (hh <= tt && i - k + 1 > q[hh]) hh++;
            while (hh <= tt && nums[q[tt]] <= nums[i]) tt--;
            q[++tt] = i;
            if (i >= k - 1) res.push_back(nums[q[hh]]);
        }
        return res;
    }
};

代码

// Created by WXX on 2021/2/24 18:43
#include <iostream>
#include <cstring>

using namespace std;

const int N = 20010;

int n, m;
int f[N], g[N], q[N];  // g存储上一行的值，f存储当前行的值，q是单调队列

int main() { 
   

    cin >> n >> m;
    for (int i = 0; i < n; i++) { 
     // 这里采取边读入物品，边处理；每个物品都要进行滑窗处理
        int v, w, s;
        cin >> v >> w >> s;
        memcpy(g, f, sizeof f);  // 将f中的数据拷贝到g中
        for (int r = 0; r < v; r++) { 
   
            int hh = 0, tt = -1;
            for (int k = r; k <= m; k += v) { 
   
                if (hh <= tt && q[hh] < k - s * v) hh++;  // 说明队头元素应该 滑出滑窗
                while (hh <= tt && g[q[tt]] - (q[tt] - r) / v * w <= g[k] - (k - r) / v * w) tt--;
                q[++tt] = k;  // 将当前考察体积存入滑窗
                if (hh <= tt) f[k] = max(f[k], g[q[hh]] + (k - q[hh]) / v * w);
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}

Java

import java.util.Scanner;

// Created by WXX on 2021/2/24 19:37
public class Main { 
   

    public static final int N = 20010;
    static int n, m;
    static int[] f = new int[N], g = new int[N], q = new int[N];

    public static void main(String[] args) { 
   

        Scanner sn = new Scanner(System.in);
        n = sn.nextInt(); m = sn.nextInt();
        for (int i = 0; i < n; i++) { 
     // 这里采取边读入物品，边处理；每个物品都要进行滑窗处理
            int v = sn.nextInt(), w = sn.nextInt(), s = sn.nextInt();
            System.arraycopy(f, 0, g, 0, N);  // 将f中的数据拷贝到g中
            for (int r = 0; r < v; r++) { 
   
                int hh = 0, tt = -1;
                for (int k = r; k <= m; k += v) { 
   
                    if (hh <= tt && q[hh] < k - s * v) hh++;  // 说明队头元素应该 滑出滑窗
                    while (hh <= tt && g[q[tt]] - (q[tt] - r) / v * w <= g[k] - (k - r) / v * w) tt--;
                    q[++tt] = k;  // 将当前考察体积存入滑窗
                    if (hh <= tt) f[k] = Math.max(f[k], g[q[hh]] + (k - q[hh]) / v * w);
                }
            }
        }
        System.out.println(f[m]);
    }
}

四. 混合背包问题

问题描述

问题链接：混合背包问题

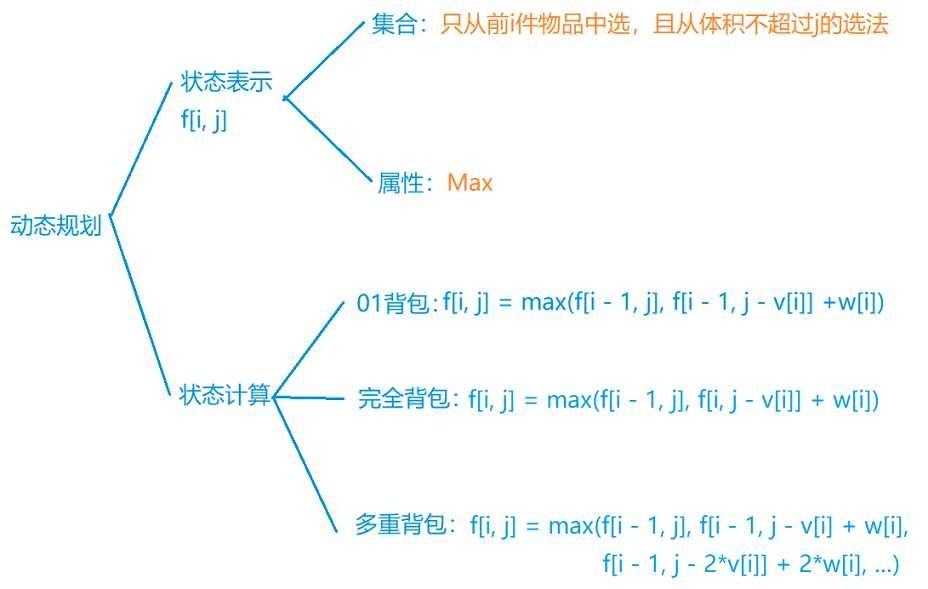
分析

分不同情况下进行状态转移即可，如下图：

代码

// Created by WXX on 2021/2/24 19:59
#include <iostream>

using namespace std;

const int N = 1010;

int n, m;
int f[N];

int main() { 
   

    cin >> n >> m;
    for (int i = 0; i < n; i++) { 
   
        int v, w, s;
        cin >> v >> w >> s;
        if (s == 0) { 
     // 完全背包
            for (int j = v; j <= m; j++) f[j] = max(f[j], f[j - v] + w);
        } else { 
   
            if (s == -1) s = 1;  // 全部转为多重背包，然后使用二进制优化
            for (int k = 1; k <= s; k *= 2) { 
   
                for (int j = m; j >= k * v; j--)
                    f[j] = max(f[j], f[j - k * v] + k * w);
                s -= k;
            }
            if (s) { 
   
                for (int j = m; j >= s * v; j--)
                    f[j] = max(f[j], f[j - s * v] + s * w);
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}

Java

import java.util.Scanner;

// Created by WXX on 2021/2/24 20:06
public class Main { 
   

    public static final int N = 1010;

    static int n, m;
    static int[] f = new int[N];

    public static void main(String[] args) { 
   

        Scanner sn = new Scanner(System.in);
        n = sn.nextInt(); m = sn.nextInt();
        for (int i = 0; i < n; i++) { 
   
            int v = sn.nextInt(), w = sn.nextInt(), s = sn.nextInt();
            if (s == 0) { 
     // 完全背包
                for (int j = v; j <= m; j++) f[j] = Math.max(f[j], f[j - v] + w);
            } else { 
   
                if (s == -1) s = 1;  // 全部转为多重背包，然后使用二进制优化
                for (int k = 1; k <= s; k *= 2) { 
   
                    for (int j = m; j >= k * v; j--)
                        f[j] = Math.max(f[j], f[j - k * v] + k * w);
                    s -= k;
                }
                if (s != 0) { 
   
                    for (int j = m; j >= s * v; j--)
                        f[j] = Math.max(f[j], f[j - s * v] + s * w);
                }
            }
        }
        System.out.println(f[m]);
    }
}

五. 二维费用背包问题

问题描述

问题链接：二维费用背包问题

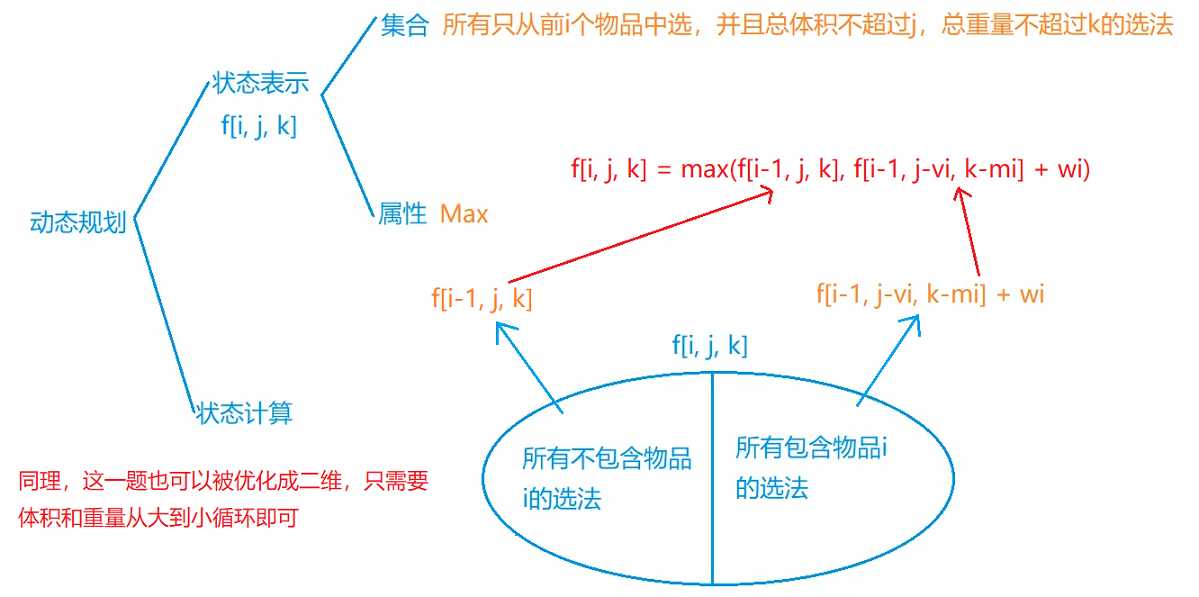
分析

需要说明一点，二维费用背包为可以和 01背包、完全背包、多重背包、分组背包 这四种类型背包中的任何一种组合起来。
当前题目是和 01背包 绑定起来的题目

代码

// Created by WXX on 2021/2/24 20:25
#include <iostream>

using namespace std;

const int N = 110;

int n, V, M;
int f[N][N];  // 第一维代表体积，第二维代表重量

int main() { 
   

    cin >> n >> V >> M;
    for (int i = 0; i < n; i++) { 
   
        int v, m, w;
        cin >> v >> m >> w;
        for (int j = V; j >= v; j--)
            for (int k = M; k >= m; k--)
                f[j][k] = max(f[j][k], f[j - v][k - m] + w);
    }
    cout << f[V][M] << endl;
    return 0;
}

Java

import java.util.Scanner;

// Created by WXX on 2021/2/24 20:34
public class Main { 
   

    public static final int N = 110;

    static int n, V, M;
    static int[][] f = new int[N][N];  // 第一维代表体积，第二维代表重量

    public static void main(String[] args) { 
   

        Scanner sn = new Scanner(System.in);
        n = sn.nextInt(); V = sn.nextInt(); M = sn.nextInt();
        for (int i = 0; i < n; i++) { 
   
            int v = sn.nextInt(), m = sn.nextInt(), w = sn.nextInt();
            for (int j = V; j >= v; j--)
                for (int k = M; k >= m; k--)
                    f[j][k] = Math.max(f[j][k], f[j - v][k - m] + w);
        }
        System.out.println(f[V][M]);
    }
}

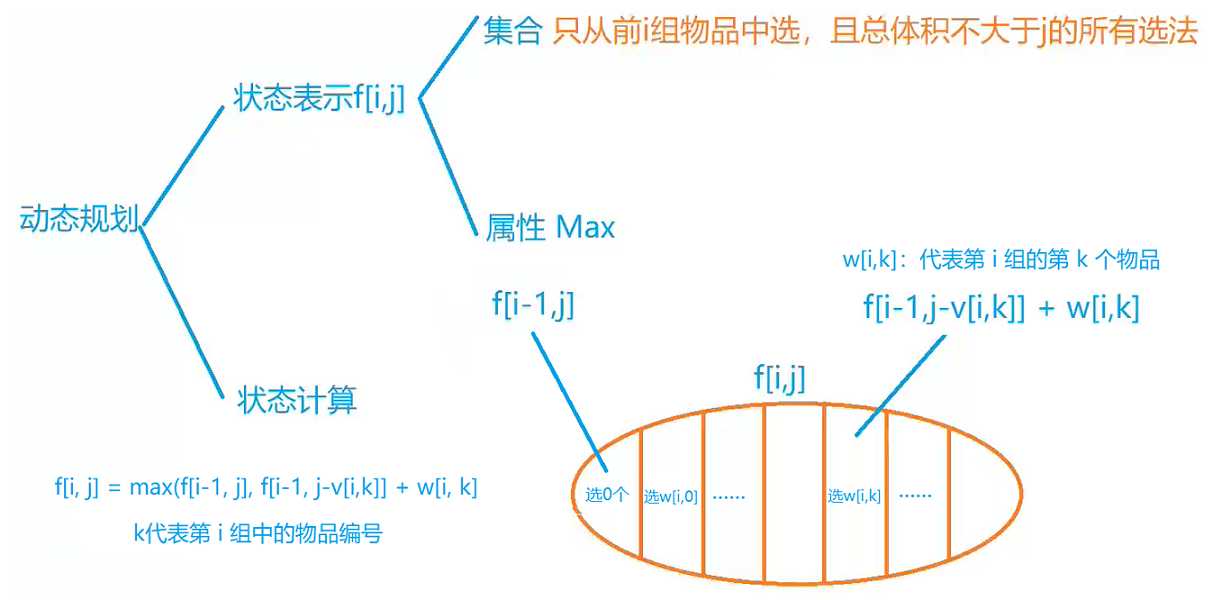
六. 分组背包问题

问题描述

问题链接：分组背包问题

分析

代码

// Created by WXX on 2021/2/24 20:52
#include <iostream>

using namespace std;

const int N = 110;

int n, m;
// s[i]: 代表第i组物品的数量；v[i][k],w[i][k]: 第i组中第k个物品的体积和价值
int v[N][N], w[N][N], s[N];
int f[N];

int main() { 
   

    cin >> n >> m;
    for (int i = 1; i <= n; i++) { 
   
        cin >> s[i];
        for (int j = 0; j < s[i]; j++)
            cin >> v[i][j] >> w[i][j];
    }

    for (int i = 1; i <= n; i++)  // 先循环物品
        for (int j = m; j >= 0; j--)  // 再循环容量。因为某件物品要么选要么不选，所以递减遍历
            for (int k = 0; k < s[i]; k++)  // 最后循环决策
                if (j >= v[i][k])
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
    cout << f[m] << endl;
    return 0;
}

Java

import java.util.Scanner;

// Created by WXX on 2021/2/24 21:01
public class Main { 
   

    public static final int N = 110;

    static int n, m;
    // s[i]: 代表第i组物品的数量；v[i][k],w[i][k]: 第i组中第k个物品的体积和价值
    static int[] s = new int[N];
    static int[][] v = new int[N][N], w = new int[N][N];
    static int[] f = new int[N];

    public static void main(String[] args) { 
   

        Scanner sn = new Scanner(System.in);
        n = sn.nextInt(); m = sn.nextInt();
        for (int i = 1; i <= n; i++) { 
   
            s[i] = sn.nextInt();
            for (int j = 0; j < s[i]; j++) { 
   
                v[i][j] = sn.nextInt(); w[i][j] = sn.nextInt();
            }
        }

        for (int i = 1; i <= n; i++)  // 先循环物品
            for (int j = m; j >= 0; j--)  // 再循环容量。因为某件物品要么选要么不选，所以递减遍历
                for (int k = 0; k < s[i]; k++)  // 最后循环决策
                    if (j >= v[i][k])
                        f[j] = Math.max(f[j], f[j - v[i][k]] + w[i][k]);
        System.out.println(f[m]);
    }
}

注意点

其实 多重背包问题 是 分组背包问题 的一个特例。

对于多重背包问题：对于某个物品来说，如果出现 s 次，则可以选择0次，(1次…s次)，我们将(1次…s次)这些情况打包起来形成一组，看成不同的物品(s个)，我们最多从中选1个，因此有 s+1 种可能的情况。

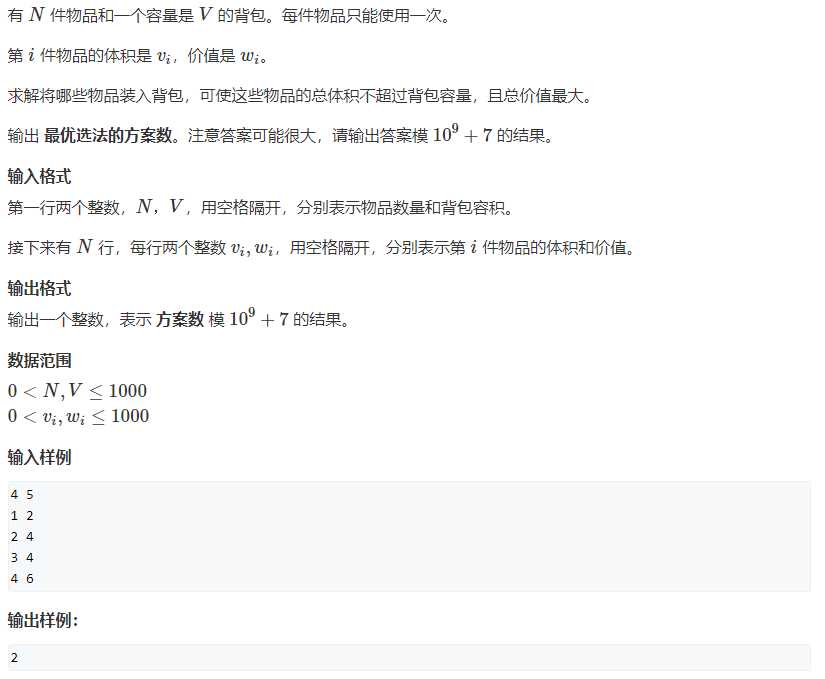
七. 背包问题求方案数

问题描述

问题链接：背包问题求方案数

分析

需要说明一点，和二维费用背包一样。背包问题求方案数可以和 01背包、完全背包、多重背包、分组背包 这四种类型背包中的任何一种组合起来。
本题的本质是求最短路径的条数。其实动态规划的本质是图论问题。
我们可以根据背包问题的状态转移方程来分析方案数，这里状态转移方程是： $f (i, j) = m a x (f (i - 1, j), f (i - 1, j - v i) + w i)$ 。为了计算方案数，这里的 $f (i, j)$ 定义需要做一下改变： $f (i, j)$ 代表只从前 i 个物品中选，体积恰好是 j 的最大价值。
为了实现 $f (i, j)$ 所定义的含义，我们需要在初始化是将 f(0, k)，即第一行初始化为负无穷，且只有 f(0, 0) = 0。这样的话，负无穷所更新的状态仍然是负无穷，只有被 f(0, 0)更新的状态是有效的状态，因此体积恰好是 j。
为了记录方案数，我们还需要另外开辟一个数组 $g (i, j)$ ，代表的含义是： $f (i, j)$ 取最大值时的方案数。 $g (i, j)$ 的求解存在三种情况：

（1）如果 $f (i - 1, j)$ > $f (i - 1, j - v) + w$ ，则 $g (i, j)$ = $g (i - 1, j)$ ；

（2）如果 $f (i - 1, j)$ < $f (i - 1, j - v) + w$ ，则 $g (i, j)$ = $g (i - 1, j - v)$ ；

（3）如果 $f (i - 1, j)$ = $f (i - 1, j - v) + w$ ，则 $g (i, j)$ = $g (i - 1, j)$ + $g (i - 1, j - v)$ ；
因为本题对应的是 01背包问题，所以上面的二维数组都可以被优化为一维数组，只要在遍历体积的时候从大到小进行遍历即可。

代码

// Created by WXX on 2021/2/24 21:56
#include <iostream>
#include <cstring>

using namespace std;

const int N = 1010, mod = 1e9 + 7;

int n, m;
// f[i]: 表示体积恰好为j时的最大价值；g[i]: f[i]取最大值时的方案数
int f[N], g[N];

int main() { 
   

    cin >> n >> m;

    memset(f, -0x3f, sizeof f);
    f[0] = 0;
    g[0] = 1;  // 什么都不选也是一种方案

    for (int i = 0; i < n; i++) { 
   
        int v, w;
        cin >> v >> w;
        for (int j = m; j >= v; j--) { 
   
            int maxv = max(f[j], f[j - v] + w);
            int cnt = 0;
            if (maxv == f[j]) cnt += g[j];
            if (maxv == f[j - v] + w) cnt += g[j - v];
            g[j] = cnt % mod;
            f[j] = maxv;
        }
    }

    int res = 0;  // 最大价值，因为取到最大价值消耗的体积不一定恰好等于背包容量
    for (int i = 0; i <= m; i++) res = max(res, f[i]);

    int cnt = 0;  // 取到最大价值的方案数
    for (int i = 0; i <= m; i++)
        if (res == f[i])
            cnt = (cnt + g[i]) % mod;
    cout << cnt << endl;
    return 0;
}

Java

import java.util.Arrays;
import java.util.Scanner;

// Created by WXX on 2021/2/24 22:08
public class Main { 
   

    public static final int N = 1010, mod = (int)(1e9 + 7);

    static int n, m;
    // f[i]: 表示体积恰好为j时的最大价值；g[i]: f[i]取最大值时的方案数
    static int[] f = new int[N], g = new int[N];

    public static void main(String[] args) { 
   

        Scanner sn = new Scanner(System.in);
        n = sn.nextInt(); m = sn.nextInt();

        Arrays.fill(f, Integer.MIN_VALUE);
        f[0] = 0;
        g[0] = 1;  // 什么都不选也是一种方案

        for (int i = 0; i < n; i++) { 
   
            int v = sn.nextInt(), w = sn.nextInt();
            for (int j = m; j >= v; j--) { 
   
                int maxv = Math.max(f[j], f[j - v] + w);
                int cnt = 0;
                if (maxv == f[j]) cnt += g[j];
                if (maxv == f[j - v] + w) cnt += g[j - v];
                g[j] = cnt % mod;
                f[j] = maxv;
            }
        }

        int res = 0;  // 最大价值，因为取到最大价值消耗的体积不一定恰好等于背包容量
        for (int i = 0; i <= m; i++) res = Math.max(res, f[i]);

        int cnt = 0;  // 取到最大价值的方案数
        for (int i = 0; i <= m; i++)
            if (res == f[i])
                cnt = (cnt + g[i]) % mod;
        System.out.println(cnt);
    }
}

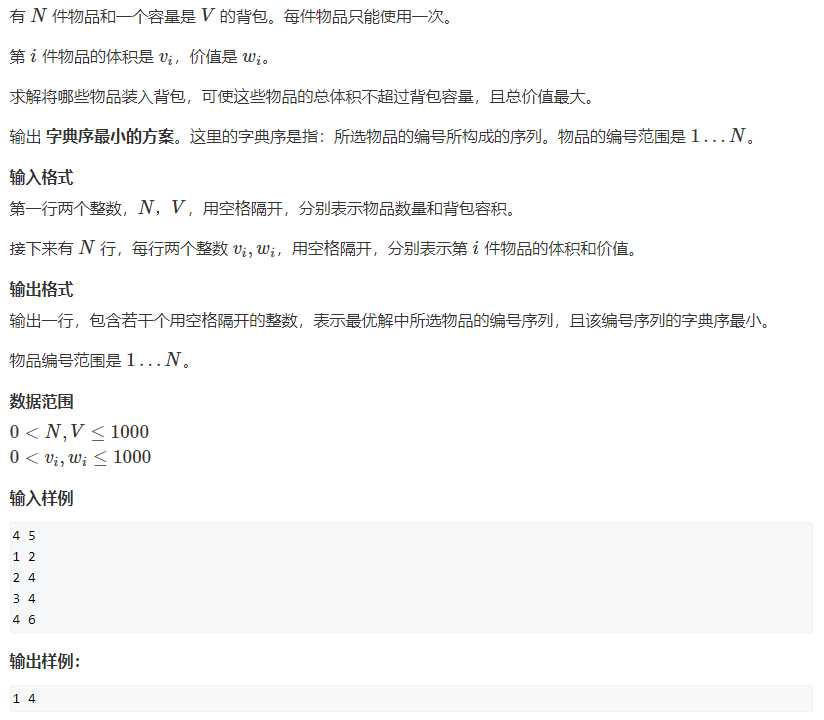
八. 求背包问题的方案

问题描述

问题链接：求背包问题的方案

分析

需要说明一点，和二维费用背包以及背包问题求方案数一样。求背包问题的方案可以和 01背包、完全背包、多重背包、分组背包 这四种类型背包中的任何一种组合起来。
我们可以根据背包问题的状态转移方程来求背包的方案，这里状态转移方程是： $f (i, j) = m a x (f (i - 1, j), f (i - 1, j - v i) + w i)$ 。这里存在三种情况

（1） $f (i, j)$ == $f (i - 1, j)$ ， $f (i, j)$ > $f (i - 1, j - v i) + w i$ ，则最大价值的方案中必定不包含物品 i ；

（2） $f (i, j)$ > $f (i - 1, j)$ ， $f (i, j)$ == $f (i - 1, j - v i) + w i$ ，则最大价值的方案中必定包含物品 i ；

（3） $f (i, j)$ == $f (i - 1, j)$ ， $f (i, j)$ == $f (i - 1, j - v i) + w i$ ，则最大价值的方案中可包含也可不包含物品 i ；
另外，本题还要求输出 字典序最小的方案，因此我们应该反过来遍历物品（从物品n开始遍历到物品1），求出数组 f 后，之后就可以从物品1开始考察，能选则选，然后考虑物品2，…，这样得到的结果字典序最小。如果还是从物品1开始遍历，则之后只能从物品n开始考察，无法保证字典序最小。
注意：我们此时不能将二维数组压缩为一维数组，这是因为数组 f 中间的状态还需要被使用。
除了上面这种解决方案外，还可以通过创建一个bool数组记录某个物品是否应该被选择。

代码

// Created by WXX on 2021/2/24 22:27
#include <iostream>

using namespace std;

const int N = 1010;

int n, m;
int v[N], w[N];
int f[N][N];

int main() { 
   

    cin >> n >> m;
    for (int i = 1; i <= n; i++) cin >> v[i] >> w[i];

    for (int i = n; i >= 1; i--)
        for (int j = 0; j <= m; j++) { 
   
            f[i][j] = f[i + 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
        }

    int j = m;
    for (int i = 1; i <= n; i++)
        if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i]) { 
   
            cout << i << ' ';  // 如果能选物品i的话一定要选，这样可保证字典序最小
            j -= v[i];
        }
    return 0;
}

Java

import java.util.Scanner;

// Created by WXX on 2021/2/24 22:33
public class Main { 
   

    public static final int N = 1010;

    static int n, m;
    static int[] v = new int[N], w = new int[N];
    static int[][] f = new int[N][N];

    public static void main(String[] args) { 
   

        Scanner sn = new Scanner(System.in);
        n = sn.nextInt(); m = sn.nextInt();
        for (int i = 1; i <= n; i++) { 
   
            v[i] = sn.nextInt(); w[i] = sn.nextInt();
        }

        for (int i = n; i >= 1; i--)
            for (int j = 0; j <= m; j++) { 
   
                f[i][j] = f[i + 1][j];
                if (j >= v[i]) f[i][j] = Math.max(f[i][j], f[i + 1][j - v[i]] + w[i]);
            }

        int j = m;
        for (int i = 1; i <= n; i++)
            if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i]) { 
   
                System.out.print(i + " ");;  // 如果能选物品i的话一定要选，这样可保证字典序最小
                j -= v[i];
            }
    }
}

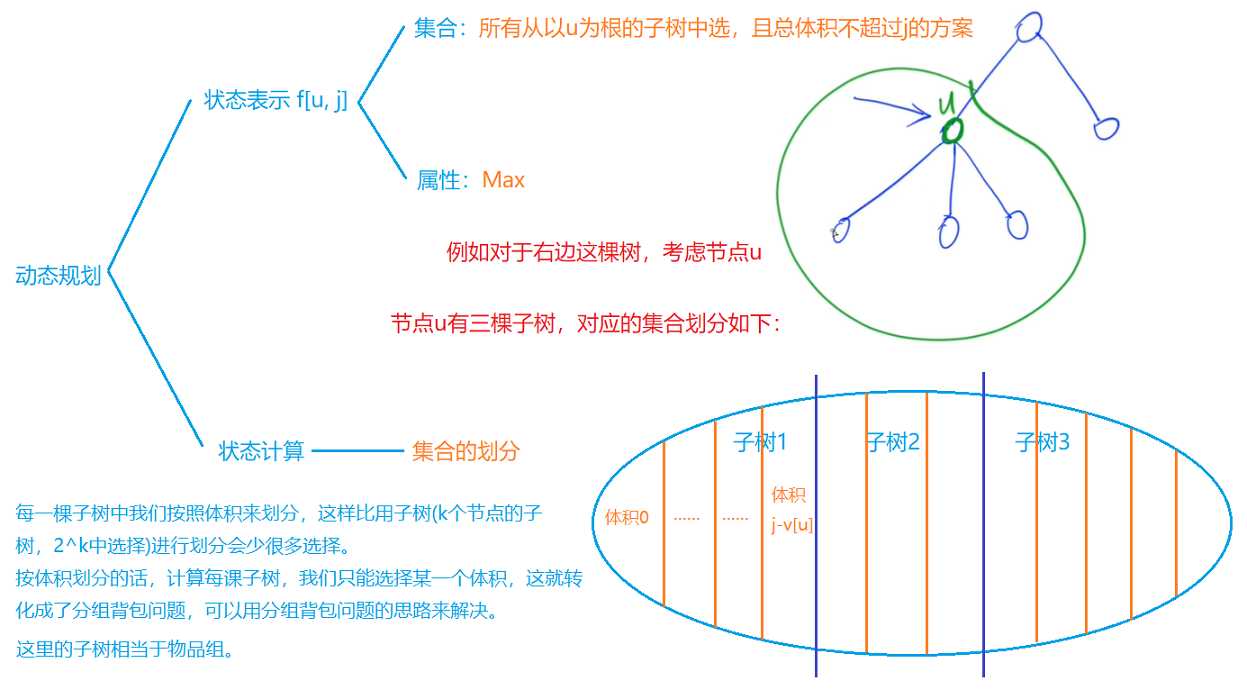
九. 有依赖的背包问题

问题描述

问题链接：有依赖的背包问题

分析

这一题是一道 树形DP 的问题
这是一棵树，我们采取的存储方式邻接表，实现方式是数组模拟链表，这部分内容可以参照AcWing的算法基础课：网址

代码

// Created by WXX on 2021/2/24 23:08
#include <iostream>
#include <cstring>

using namespace std;

const int N = 110;

int n, m;
int v[N], w[N];
int h[N], e[N], ne[N], idx = 0;  // 邻接矩阵
int f[N][N];

void add(int a, int b) { 
   
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int u) { 
   

    for (int i = h[u]; ~i; i = ne[i]) { 
     // 遍历u的子节点，相当于循环物品组
        int son = e[i];
        dfs(son);  // 求解完成子节点后才能求解当前节点

        // 分组背包
        for (int j = m - v[u]; j >= 0; j--)  // 循环体积
            for (int k = 0; k <= j; k++)  // 循环决策
                f[u][j] = max(f[u][j], f[u][j - k] + f[son][k]);
    }

    // 将物品u加进去
    for (int i = m; i >= v[u]; i--) f[u][i] = f[u][i - v[u]] + w[u];
    for (int i = 0; i < v[u]; i++) f[u][i] = 0;  // 不能放入物品u，则整棵子树都不能放入
}

int main() { 
   

    cin >> n >> m;
    memset(h, -1, sizeof h);
    int root = 1;  // 根节点并不一定是1号点
    for (int i = 1; i <= n; i++) { 
   
        int p;
        cin >> v[i] >> w[i] >> p;
        if (p == -1) root = i;
        else add(p, i);  // 添加一条由p指向i的边
    }
    dfs(root);
    cout << f[root][m] << endl;
    return 0;
}

Java

import java.util.Arrays;
import java.util.Scanner;

// Created by WXX on 2021/2/24 23:24
public class Main { 
   

    public static final int N = 110;

    static int n, m;
    static int[] v = new int[N], w = new int[N];
    // 邻接矩阵
    static int[] h = new int[N], e = new int[N], ne = new int[N];
    static int idx = 0;

    static int[][] f = new int[N][N];

    private static void add(int a, int b) { 
   
        e[idx] = b; ne[idx] = h[a]; h[a] = idx++;
    }

    private static void dfs(int u) { 
   

        for (int i = h[u]; i != -1; i = ne[i]) { 
     // 遍历u的子节点，相当于循环物品组
            int son = e[i];
            dfs(son);  // 求解完成子节点后才能求解当前节点

            // 分组背包
            for (int j = m - v[u]; j >= 0; j--)  // 循环体积
                for (int k = 0; k <= j; k++)  // 循环决策
                    f[u][j] = Math.max(f[u][j], f[u][j - k] + f[son][k]);
        }

        // 将物品u加进去
        for (int i = m; i >= v[u]; i--) f[u][i] = f[u][i - v[u]] + w[u];
        for (int i = 0; i < v[u]; i++) f[u][i] = 0;  // 不能放入物品u，则整棵子树都不能放入
    }

    public static void main(String[] args) { 
   

        Scanner sn = new Scanner(System.in);
        n = sn.nextInt(); m = sn.nextInt();
        Arrays.fill(h, -1);
        int root = 1;  // 根节点并不一定是1号点
        for (int i = 1; i <= n; i++) { 
   
            v[i] = sn.nextInt(); w[i] = sn.nextInt();
            int p = sn.nextInt();
            if (p == -1) root = i;
            else add(p, i);  // 添加一条由p指向i的边
        }
        dfs(root);
        System.out.println(f[root][m]);
    }
}

LeetCode上一些背包问题

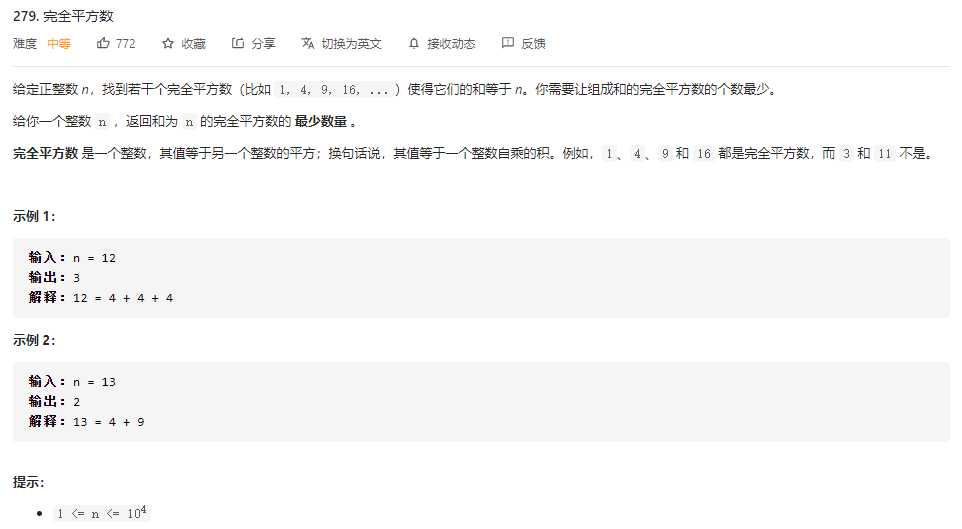
Leetcode 0279 完全平方数

问题描述

问题链接：Leetcode 0279 完全平方数

分析

完全背包问题，把n当做背包容量，每个完全平方数当做物品，其对应的数值数值当做体积，每个数的价值都为1，则问题变成在恰好装满背包的情况下，总价值最少是多少。完全背包问题的时间复杂度为O(体积*物品个数)，所以该题的时间复杂度为 $\sqrt n)$ 。

代码

/** * 执行用时：204 ms, 在所有 C++ 提交中击败了69.60%的用户 * 内存消耗：8.7 MB, 在所有 C++ 提交中击败了83.16%的用户 */
class Solution { 
   
public:
    int numSquares(int n) { 
   

        vector<int> f(n + 1, 1e9);  // f[i] 代表 i 最少可以由几个完全平方数表示
        f[0] = 0;
        for (int i = 1; i * i <= n; i++)  // 先循环物品 i*i
            for (int j = i * i; j <= n; j++)  // 再循环体积：体积从i*i开始
                f[j] = min(f[j], f[j - i * i] + 1);
        return f[n];
    }
};

Java

/** * 执行用时：30 ms, 在所有 Java 提交中击败了86.04%的用户 * 内存消耗：37.8 MB, 在所有 Java 提交中击败了34.09%的用户 */
public class Solution { 
   
    public int numSquares(int n) { 
   
        
        int[] f = new int[n + 1];
        Arrays.fill(f, Integer.MAX_VALUE);
        f[0] = 0;
        for (int i = 1; i * i <= n; i++)  // 先循环物品 i*i
            for (int j = i * i; j <= n; j++)  // 再循环体积：体积从i*i开始
                f[j] = Math.min(f[j], f[j - i * i] + 1);
        return f[n];
    }
}

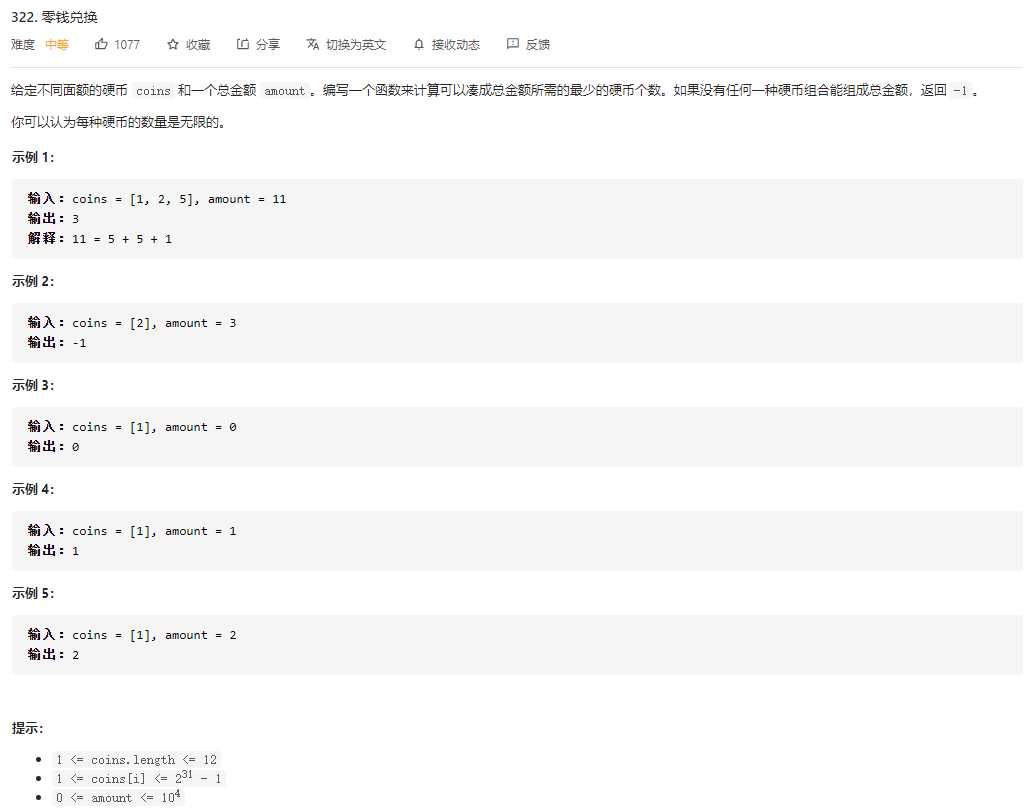
Leetcode 0322 零钱兑换

问题描述

问题链接：Leetcode 0322 零钱兑换

分析

完全背包问题
amout为容量；物品体积为coins[i]，价值为1
和上一题十分类似，这里就不详细分析了

代码

/** * 执行用时：64 ms, 在所有 C++ 提交中击败了89.56%的用户 * 内存消耗：13.7 MB, 在所有 C++ 提交中击败了66.94%的用户 */
class Solution { 
   
public:
    int coinChange(vector<int> &coins, int m) { 
   

        vector<int> f(m + 1, 1e8);
        f[0] = 0;
        for (auto v : coins)
            for (int j = v; j <= m; j++)
                f[j] = min(f[j], f[j - v] + 1);
        if (f[m] == 1e8) return -1;
        return f[m];
    }
};

Java

/** * 执行用时：12 ms, 在所有 Java 提交中击败了94.69%的用户 * 内存消耗：38.1 MB, 在所有 Java 提交中击败了22.43%的用户 */
public class Solution { 
   
    public int coinChange(int[] coins, int m) { 
   

        int[] dp = new int[m + 1];
        Arrays.fill(dp, m + 1);
        dp[0] = 0;
        for (int v : coins)
            for (int j = v; j <= m; j++)
                dp[j] = Math.min(dp[j], dp[j - v] + 1);

        return dp[m] == m + 1 ? -1 : dp[m];
    }
}

今天的文章背包问题（背包九讲）分享到此就结束了，感谢您的阅读。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/24179.html

背包问题（背包九讲）

背包九讲

概述

一. 01背包问题

二. 完全背包问题

三. 多重背包问题

3.1 多重背包问题 I

3.2 多重背包问题 II

3.2 多重背包问题 III

四. 混合背包问题

五. 二维费用背包问题

六. 分组背包问题

七. 背包问题求方案数

八. 求背包问题的方案

九. 有依赖的背包问题

LeetCode上一些背包问题

Leetcode 0279 完全平方数

Leetcode 0322 零钱兑换

相关推荐

发表回复