动态规划算法解决背包问题

一、动态规划算法概述

动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题，先求解子问题，然后从子问题解得到原问题解。

但是经分解得到的子问题往往不是互相独立的。不同子问题的数目常常只有多项式量级。在用分治法求解极值问题时，有些子问题被重复计算了许多次。

如果能够保存已解决的子问题的答案，而在需要时再找出已求得的答案，就可以避免大量重复计算，从而得到多项式时间算法。

动态规划 VS 分治法：

• 相同点：基本思想均是将原问题分解成若干个子问题，先求子问题，然后从子问题的解得到原问题的解；
• 不同点：
  • 适用于动态规划求解的问题，分解得到的子问题往往不是互相独立的；
  • 动态规划为自底向上，而分治法为自顶向下。

当分解出的子问题不相互独立的话，若使用分治法来求解此类问题，会导致使用指数级的运行时间，而子问题的个数只有多项式量级。所以，此类问题不适合使用分治法。

动态规划是如何减少对重复子问题求解的呢？

答案是保存已求解的子问题的解，在需要时找出，从而避免大量的重复计算得到多项式的运行时间；通常用一个表来记录所有已解决的子问题。

动态规划算法通常用于求解具有某种最优性质的问题。

二、背包问题

2.1 什么是背包问题

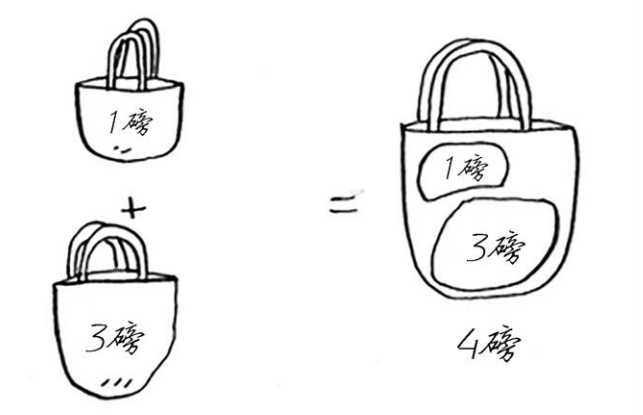
今年的年会，聪明大方的老板为了激励员工，决定买三种类型的奖品奖励给勤奋的员工小王。

为了让自己不至于放血太多又不会显得太抠门，美其名曰考验员工小王的智商。机智的老板想到了一个好法子：给小王发一个最大能装下 4 磅物品的背包，只有装到背包中的物品才归属于小王。

如果你是员工小王，怎么装才能得到最大的物品价值呢？

2.2 背包问题思路分析

首先，最容易想到的方法，就是计算出各种可能的奖品组合的情况，找出价值最高的组合放入到背包中。对于三种奖品，共有 8 种的组合，对于四种奖品，共有 16 种组合。每增加一种奖品，需要计算的组合数都将翻倍。如果明年老板决定奖励十一种奖品给小王，那小王最好还是放弃奖品算了。我们可以看到，这种算法的时间复杂度为 O(2ⁿ)，效率较低。

如何找到最优解呢？答案是使用动态规划。

对于背包问题，可以先解决小背包（子背包）的问题，然后逐步解决原来的问题。

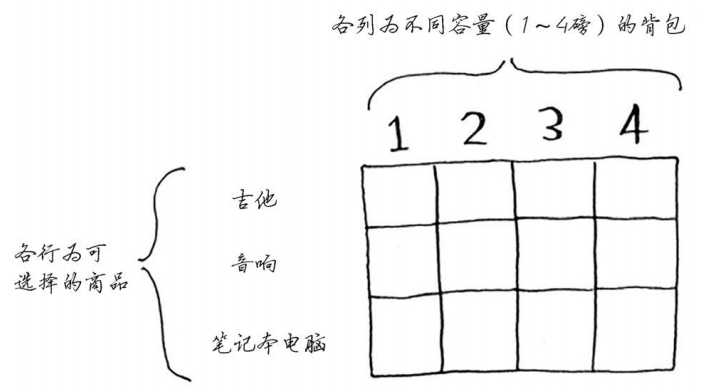
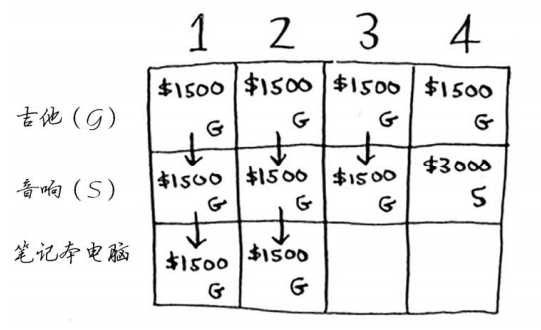
每个动态规划算法都从一个网格开始，背包问题的网格如下。

网格的各行为奖品，各列为不同容量（1～4磅）的背包。所有这些列都是必要的，因为它们将用于计算子背包中的物品价值。

第一步：

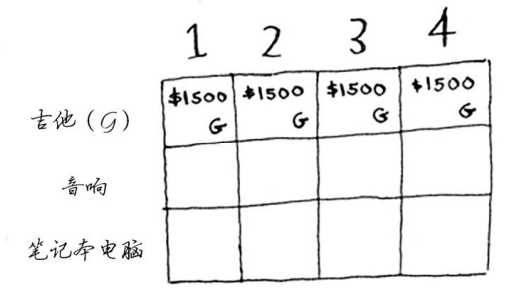
我们首先假设可选择的奖品只有吉他（1 磅）。当背包的容量为 1 时，刚好放下一个吉他，此时背包价值为 1500。当背包的容量为 2、3、4 时，由于可选的商品只有吉他且同样的奖品只能拿一件，因此即便会使背包的空间浪费，背包中仍然是只能放一个吉他，背包中的价值仍然为 1500。

第二步：

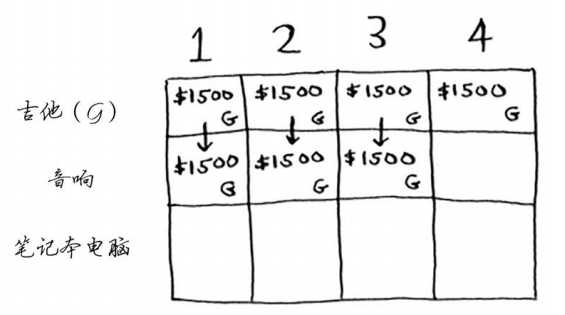
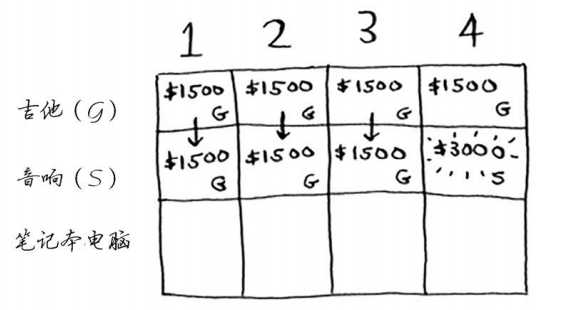
我们再假设可选的商品只有吉他（1 磅）和音响（4 磅）。当背包的容量为 1、2、3 时，由于音响的重量为 4，因此无法放入到背包中，背包中只能放入一个吉他。

当背包的容量为 4 时，刚好等于音响的重量。这个时候有两个选择：一是只放入一个吉他；二是只放入一个音响。由于音响的价值为 3000，大于吉他的价值，因此选择将音响放入背包，此时背包中的价值为 3000。

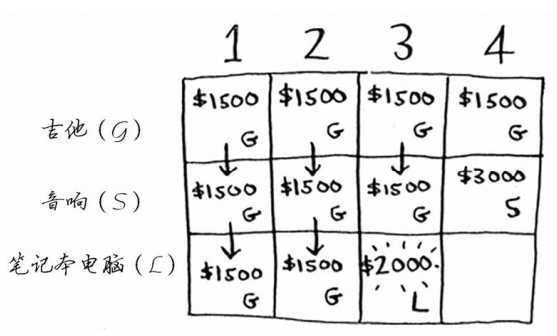
第三步：

我们在假设可选择商品有吉他（1 磅）、音响（4 磅）、笔记本电脑（3 磅）。当背包的容量为 1、2 时，毫无疑问，背包中只能放一个吉他。此时背包的价值为 1500。

当背包的容量为 3 时，有两种选择：一是只放入一个吉他；二是只放入一个电脑。由于电脑的价值高于吉他，因此将电脑放入。此时背包的价值为 2000。

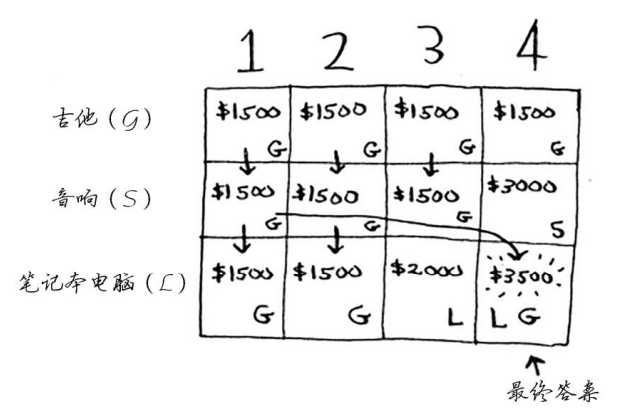
当背包的容量为 4 时，仍然有两种选择：一是放入一个吉他和电脑；二是只放入一个音响。由于吉他和电脑的总价值高于音响的价值，因此将吉他和电脑放入。此时背包的价值为 1500 + 2000 = 3500。

因此，将吉他和笔记本电脑装入背包时价值最高，这就是小王的最优解。

总结：

那么这个过程，如何用数学公式表达呢？

我们首先约定一共有 N 件物品，第 i 件物品的重量为 w[i]，价值为 v[i]，背包的承载上限为 W。再约定一个状态 cell[i][j] 表示将前 i 件（这里的前 i 件指的是有 i 件可选）物品装进限重为 j 的背包可以获得的最大价值（0<=i<=N、0<=j<=W）。

那么我们可以将 cell[0][0...W] 初始化为 0，表示将前 0 个物品装入书包的最大价值为 0。

当 i>0 时，cell[i][j] 有两种情况：

1. 不装入第 i 件物品，则背包最大价值就是相同背包容量下只有 i-1 件物品可选时的最大价值，即 cell[i-1][j]；
2. 装入第 i 件物品（若背包容量够），则最大价值为当前物品价值加背包剩余容量的最大价值，即 v[i] + cell[i-1][j-w[i]]。

那么 cell[i][j] 的值，就是这两种情况下的最大值。由此可以得到方程：
$$cell[i][j]=max\{\begin{array}{rl}& cell[i-1][j]\\ & cell[i-1][j-w[i]]+v[i]\end{array}j>=w[i]$$
求得所有的 cell[i][j] 之后，最后一个值就是背包问题的最大值。

2.3 背包问题代码实现

public static void main(String[] args) { 
   
    int[] w = { 
   0, 1, 4, 3};    // 物品的重量
    int[] v = { 
   0, 1500, 3000, 2000};    // 物品的价值

    int num = w.length; // 物品的数量可能的个数 (0~3，共 3 个)
    int weight = 5; // 背包的容量可能的个数 (0~4，共 5 个)

    int[][] cell = new int[num][weight];    // cell[i][j] 表示前i个物品可选，背包容量为j时的最大价值
    int[][] record = new int[num][weight];  // record[i][j] 用于标记第i个物品有没有放入容量为j的背包

    for (int i=1; i<num; i++){ 
     // 遍历物品
        for (int j=1; j<weight; j++){ 
      // 遍历背包容量
            if (w[i]>j){ 
       // 如果当前物品重量大于背包容量
                cell[i][j] = cell[i-1][j];  // 不装入
            }else{ 
     // 如果当前物品重量小于等于背包容量
                int value_1 = cell[i-1][j]; // 不放入第 i 个物品的背包价值
                int value_2 = v[i] + cell[i-1][j-w[i]]; // 放入第 i 个物品后的价值
                /* 把最大价值放入背包 */
                if (value_1 > value_2){ 
   
                    cell[i][j] = value_1;
                }else{ 
   
                    cell[i][j] = value_2;
                    record[i][j] = 1;   // 用于标记在本网格放入了第 i 个物品
                }
            }
        }
    }

    // 最后一个网格就是最大价值
    System.out.println("背包价值为：" + cell[num-1][weight-1]);

    // 由于最后一个网格就是最大价值
    // 因此，逆序遍历 record 找到最后一个放入的物品，然后找到剩余空间价值是放入第几个物品
    int i = record.length-1;
    int j = record[0].length-1;
    while (i > 0 && j > 0){ 
   
        if (record[i][j] == 1){ 
   
            System.out.printf("放入了第 %d 个商品\n", i);
            j = j - w[i];   // 背包剩余容量
        }
        i--;
    }
}

运行结果如下：

【注】：本文的图大多出自《算法图解》。

今天的文章动态规划算法解决背包问题分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。