二叉查找树的编程与实现 C语言

一 、目的：

1. 掌握二叉查找树的基本概念及其基本操作的实现；

二 、环境：

operating system version：Win11

CPU instruction set:  x64

Integrated Development Environment：Viusal Studio 2022

三 、内容：

输入数据的第一行为一个正整数T，表示测试数据的组数，即共 T 组测试数据。每组测试数据的第一行输入正整数 n(5 ≤n ≤20)，第二行输入n个整数，要求依次完成以下工作：

1）以这n个整数生成一棵用链式存储结构存储的二叉排序树

2）按递增顺序输出该二叉排序树中所有数

3）输入一个整数key ，对该二叉排序树进行查找，若在该二叉排序树中存在这个整数key ，则输出find ，否则输出not find；

4）输入一个整数key，若该二叉排序树中不存在这个整数key，则将key 插入到该二叉排序树中，使插入后仍为原性质的二叉排序树 否则不必插入；

5）在 4）的基础上，按递减顺序输出该二叉排序树中的所有数。

四 、要求：

1）实现二叉查找树的定义；

2）实现二叉查找树的查找、插入操作。

五 、步骤：

1.程序：

#include<stdio.h>  
typedef struct node  
{  
int data;//定义数据域  
struct node* lchild, * rchild;//指向左右结点的指针  
} nodeb,*bitree;//定义二叉排序树的结点结构  
  
void inOrder(bitree t, int* i)  
{//中序遍历  
    if (t)  
    {  
        inOrder(t->lchild, i);   
        (*i)++;  
        if (*i == 1)  
            printf("%d ", t->data);  
        else  
            printf("%d ", t->data);  
        inOrder(t->rchild, i);  
    }  
}  
  
void destOrder(bitree t, int* i)  
{//递减输出  
    if (t)  
    {  
        destOrder(t->rchild, i);  
        (*i)++;  
        if (*i == 1)  
            printf("%d ", t->data); else  
            printf("%d ", t->data);  
        destOrder(t->lchild, i);  
    }  
}  
  
void searchNode(bitree t, bitree* f, bitree* p, int key)   
{  
    *p = t;   
    *f = NULL;  
    while (*p != NULL && ((*p)->data != key))   
    {//在二叉树t中查找整数为key的结点，若找到，则p指向该结点。  
        *f = *p;  
        if (key < (*p)->data) //寻找的key小于该数  
            *p = (*p)->lchild; //在左子树中寻找  
        else  
            (*p) = (*p)->rchild;//否则在右子树中寻找  
    }  
}  
bitree createBtree(int n)  
{//建立有n个整数的二叉树  
    bitree p, q, f, t;   
    int i, d;  
    t = NULL;  
    for (i = 0; i < n; i++)   
   {  
    p = NULL;   
    scanf_s("%d", &d);  
    searchNode(t, &f, &p, d);  
    if (!p) //当该数在二叉排序树中不存在  
    {  
        q = new nodeb; //建立新节点  
        q->data = d; //并对该节点赋值  
        q->lchild = q->rchild = NULL; //令左右节点为空  
        if (f == NULL)  
            t = q;  
        else if (d < f->data)  
            f->lchild = q;   
        else  
            f->rchild = q;  
       }  
    }  
    return t;  
}  
int insertNode(bitree* t, int key)  
{//在二叉排序树中插入key结点，返回操作结果情况  
    bitree p, f, s;  
    searchNode(*t, &f, &p, key);   
    if (!p)  
    {//思路同上  
        s = new nodeb;  
        s->data = key;  
    s->lchild = s->rchild = NULL;   
    if (!f)  
        *t = s;  
    else if (key < f->data)  
        f->lchild = s;  
    else  
        f->rchild = s; return 1;  
}  
else  
  return 0;  
}  
  
int main()  
{  
    bitree t, p, f;  
    int d, j, n, key, i;  
    scanf_s("%d", &d);//输入数据的组数  
    for (j = 0; j < d; j++) {  
        scanf_s("%d", &n);  
        t = createBtree(n);  
        //调用createbintree()算法建立二叉排序树t  
        i = 0;  
        inOrder(t, &i);  
        //调用改进中序遍历按递增顺序输出该二叉排序树中的元素  
        printf("\n");  
        scanf_s("%d", &key);  
        searchNode(t, &f, &p, key);  
        //调用searchNode()算法查找要查找的整数  
        if (p)  
            printf("find\n");  
        //输出查找的结果  
        else  
            printf("not find\n");  
        scanf_s("%d", &key);  
        insertNode(&t, key);  
        i = 0;  
        //调用改进的遍历算法按递减顺序输出二叉排序树的元素  
        destOrder(t, &i);  
        printf("\n");  
    }  
    return 1;  
}  

2.程序结果：
程序运行，在此次、中我使用的测试数据如下：

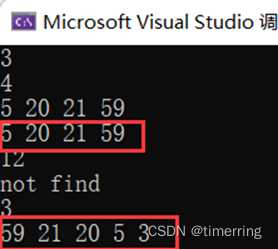
3 //数据的组数
//第一组测试数据：
4
5 20 21 59
12
3

测试结果如下：
 
分析：可知，先输入该树共4个整数，调用createbintree()算法建立二叉排序树t，然后调用改进中序遍历按递增顺序输出该二叉排序树中的元素，再输入测试样例12，调用searchNode()算法查找到，该树的结点中无12，因此输出not find，再输入测试样例3，同样该树的结点中不存在3，因此将3插入树中，最后调用改进的遍历算法按递减顺序输出二叉排序树的元素为59 21 20 5 3。

//第二组测试数据：
5
20 22 5 2 13
13
14 

测试结果如下：
 
分析：先输入该树共5个整数，调用createbintree()算法建立二叉排序树t，然后调用改进中序遍历按递增顺序输出该二叉排序树中的元素，再输入测试样例13，调用searchNode()算法查找到，该树的结点中存在13，因此输出find，再输入测试样例14，同样该树的结点中不存在14，因此将14插入树中，最后调用改进的遍历算法按递减顺序输出二叉排序树的元素。

//第三组测试数据：
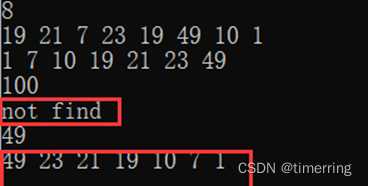
8
19 21 7 23 19 49 10 1
100
49

测试结果如下：
 
分析：先输入该树共8个整数，调用createbintree()算法建立二叉排序树t，然后调用改进中序遍历按递增顺序输出该二叉排序树中的元素，再输入测试样例100，调用searchNode()算法查找到，该树的结点中无100，因此输出not find，再输入测试样例49，该树的结点中存在49，因此无需插入，最后调用改进的遍历算法按递减顺序输出二叉排序树的元素。
由测试结果可知，算法实现了1）实现二叉查找树的定义；2）实现二叉查找树的查找、插入操作。
 

3.分析和改进：
        分析：此次、的整体思路是：首先建立二叉排序树，并且对于输入的关键字序列中的每一个整数,在正在建立的二叉排序树中查找是否已经存在该整数，若不存在，则由查找模块返回要增加结点位置的双亲结点，根据要建立的二叉排序树的性质，当要增加的整数比双亲结点的整数小的话就插到其左孩子的位置，否则插到其右孩子的位置。这样重复，直到输入结束。
在二叉排序树中进行查找的过程和二分查找类似，也是一个逐步缩小查找范围的过程。若查找成功，则是走了一条从根结点到待查结点的路径；若查找失败，则是走了一条根结点到某个叶子结点的路径。因此，查找过程中和关键字比较的次数不超过树的深度。这过程中，每进入子树前，保存当前结点，以便带回要增加结点的双亲结点。搜索直至找到要查找的整数，用一指针带回;或搜索直至叶子结点的下方，找不到要查找的整数而使空指针带回，以便判断要查找的整数是否找到。
由于含有n个结点的二叉排序树不唯一，形态和深度可能不同。故含有n个结点的二叉排序树的平均查找长度和树的形态有关。
        在递增输出的算法中，可以利用二叉排序树的一个巧妙性质，即通过中序遍历二叉搜索树得到的关键码序列是一个递增序列，以此实现递增输出。而在递减输出中，可以采用先遍历右子树，再输出结点，然后遍历左子树的方式实现递减序列的打印。
在插入算法中，在二叉排序树中插入新结点，要保证插入后的二叉树仍符合二叉排序树的定义。插入过程：若二叉排序树为空，则待插入结点*S作为根结点插入到空树中；当非空时，将待插结点关键字S->key和树根关键字t->key进行比较，若s->key = t->key,则无须插入，若s->key< t->key,则插入到根的左子树中，若s->key> t->key,则插入到根的右子树中。而子树中的插入过程和在树中的插入过程相同，如此进行下去，直到把结点*s作为一个新的树叶插入到二叉排序树中，或者直到发现树已有相同关键字的结点为止。
        改进：在基于二叉排序树的查找算法里，最后得到的时间复杂度是在O(log2(n))到O(n)之间，但是当二叉排序树只有一颗子树的时候，排序二叉树的查找就退化成了顺序查找，因此算法的效率反而不高，发现可以控制二叉排序树，让二叉排序树的左右子树均衡一些，可以让二叉排序树的左右子树的节点数目相差的绝对值不超过1，就控制住了二叉排序树的左右子树均衡程度，使基于二叉排序树的查找不至于退化成了顺序查找。我查了一下，这就是平衡二叉排序树（AVL树）的思想，即平衡二叉排序树左右子树高度差的绝对值小于或者等于1，平衡二叉排序树的左右子树也是一颗平衡二叉排序树。它的基本实现原理为在构建二叉排序树的过程中，每当插入一个结点时，先检查是否因插入而破坏了树的平衡性，若是，则找出最小不平衡子树。在保持二叉排序树特性的前提下，调整最小不平衡子树中各结点之间的链接关系，进行相应的旋转，使之成为新的平衡子树。

六 、小结：
        此次是有关二叉排序树，二叉排序树是一种动态树表。 二叉排序树的定义：二叉排序树或者是一棵空树， 或者是一棵具有如下性质的二叉树： ⑴ 若它的左子树非空，则左子树上所有结点的值均小于根结点的值； ⑵ 若它的右子树非空，则右子树上所有结点的值均大于根结点的值； ⑶ 左、右子树本身又各是一棵二叉排序树。二叉排序树的性质： 按中序遍历二叉排序树，所得到的中序遍历序列是一个递增有序序列，在对遍历进行略微的改进后，实现了递减有序序列的输出。插入、查找算法在上一部分进行了详细地分析。最后，在算法的改进部分，我针对查找算法进行了分析，当二叉排序树只有一颗子树的时候，排序二叉树的查找就退化成了顺序查找，最坏情况下效率降至O(n)，我找到了改进方案，即控制住二叉排序树的左右子树均衡程度，采用平衡二叉排序树（AVL树）的思想改进查找算法的时间复杂度。

今天的文章二叉查找树的编程与实现 C语言分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。