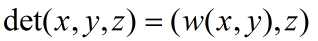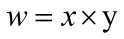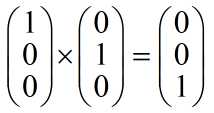本节定义向量的乘法运算:向量积
1 向量积
设T是3×3矩阵.各列分别是x,y,z:
固定x,和y时T的行列式是z的线性函数:
根据定理5,任意线性函数都可以表示成标量积:
其中w是依赖于x和y的向量:
综合以上两式可得:
w是x和y的双线性函数,于是可以将w写成x和y的乘积记做:
称为向量积.
2 向量积的性质
(i) 向量积具有反对称性
(ii)X x Y与X和Y都正交
(iii)设T是R^3中的一个旋转.则:
(iv)
(v)
(vi)

今天的文章线性代数(五十) :向量积分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/25328.html