信号的采样与混叠(时域)
在一定条件下,一个连续的时间信号完全可以用该信号在等时间间隔上的样本来表示,并且可以用这些样本的值把该信号完全恢复出来。这一非常重要的发现被称之为采样定理。
采样定理在连续时间信号(一个是连续的波形)和离散时间信号(一个是数组)之间架起了一座桥梁!!!(就好像微积分基本定理一样,把斜率和面积这两个毫不相干的概念紧密的联系在了一起。)
一维信号的采样:
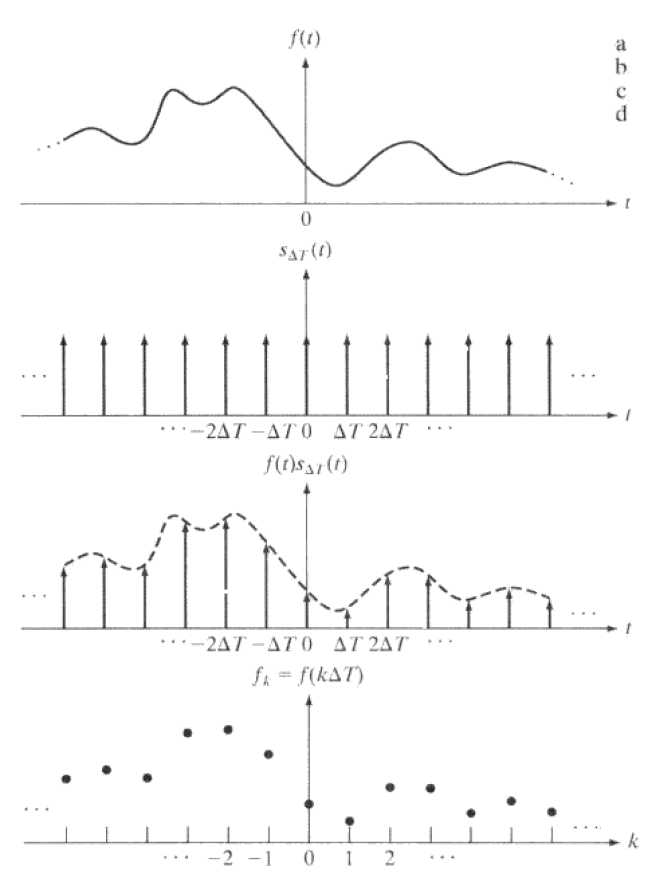
通过一个固定周期的冲击串来实现信号的采样(即,连续信号的离散化)。如下图,一个本来是连续的一维信号被分割成了很多小块,这非常像黎曼积分(Riemann integral),定积分作黎曼和的极限!
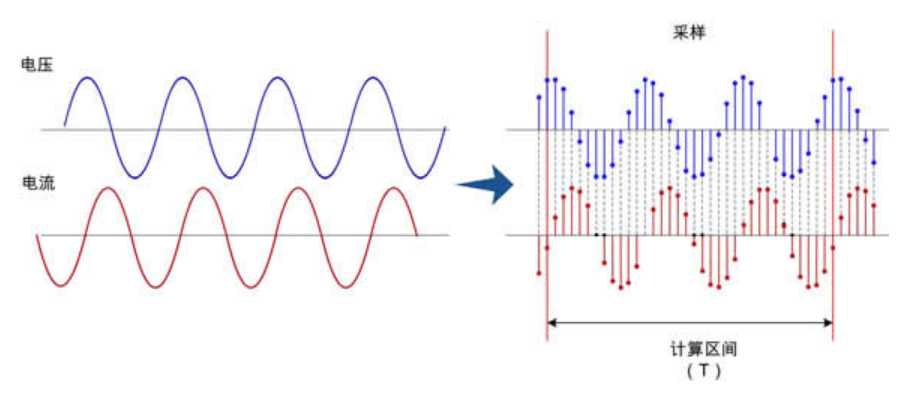
上图中原来是连续的数据通过等间隔(采样周期为T)的采样,被分割成了等间隔,具有不同幅度的冲击串,见下图。
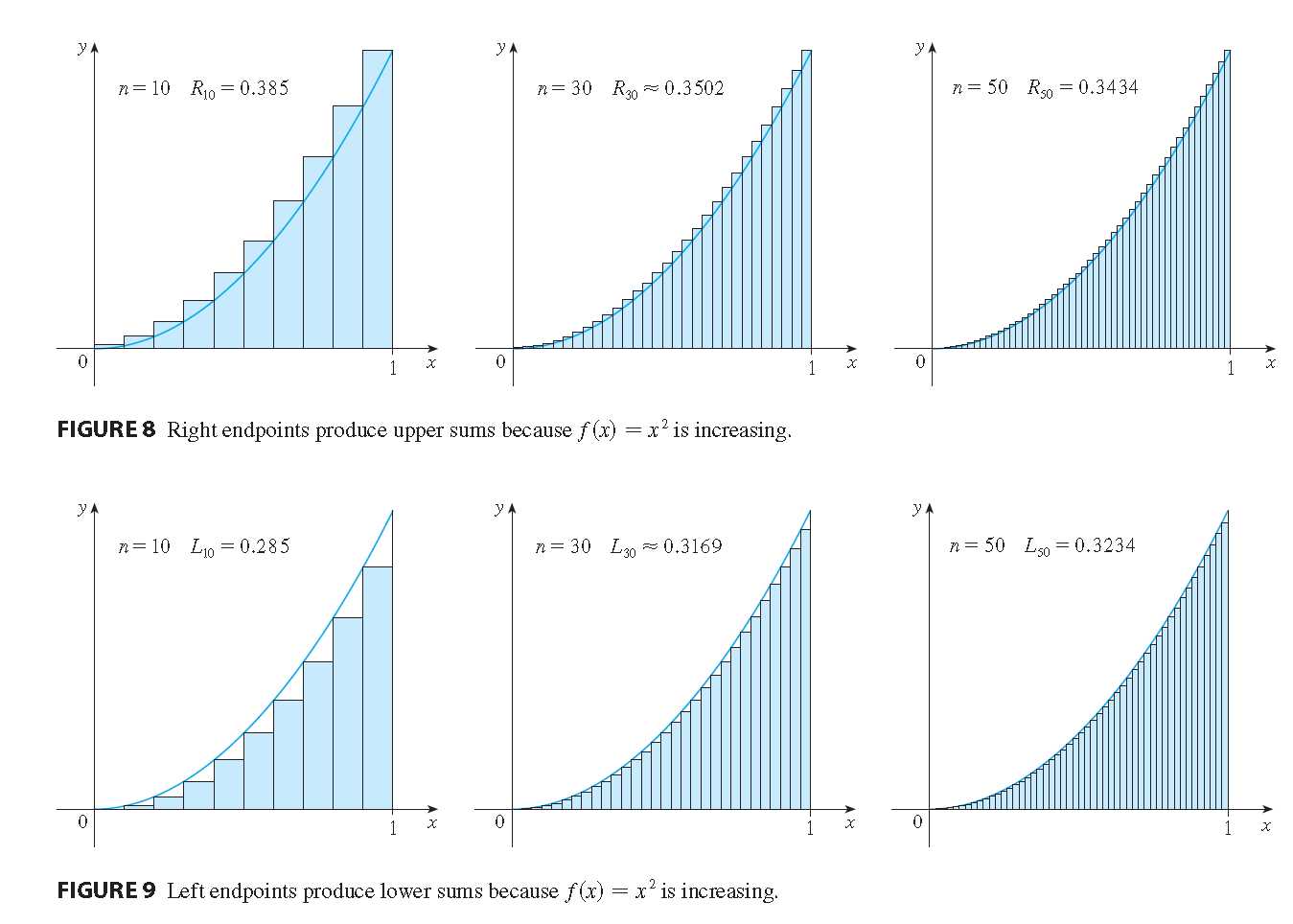
附:下图为黎曼和的极限,图中矩形的宽度就好比是采样间隔T!
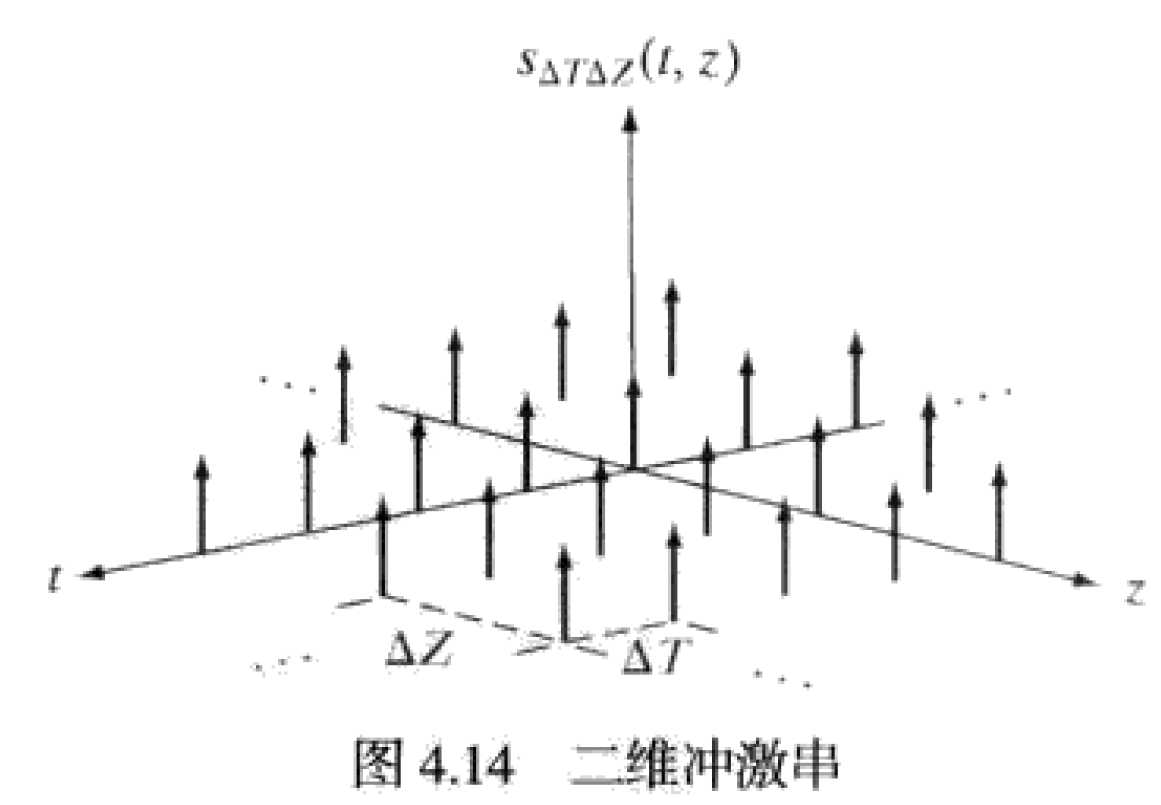
二维信号的采样:
二维信号的采样常被用于图像的数字化,相对于一维采样,他只是增加了采样的维度。不仅在X方向采样还在Y方向采样,采样后的结果是一个二维矩阵,矩阵中的每一个点代表了该位置的响应灰度。
例如,在出版业里,一幅图是由很多很小的采样点构成的,如果这些采样点的间距很小,小到你无法用肉眼分辨的话。(或者说,即便报纸上的采样点间距不是很小,但是读者眼睛距离报纸不是很近的话。)那么,报纸上的照片在我们看来就是一幅连续的图片。但是,如果你拿着放大镜或者眼睛靠着很近观察的话,你就会发现报纸上的一幅图像其实是由一个个等间隔的离散化的点拼出来的。
下面我们用Matlab软件来仿真信号的采样,以及如果采样频率(采样周期的倒数)不能满足一定要求是所带来的混叠。
Tips : 本文的后面会有一个录像说明,现在的MATLAB仿真和录像说明有一个很大的不同就是。这里的仿真是保持原始信号的频率Fo不变,不断地改变采样频率Fs.
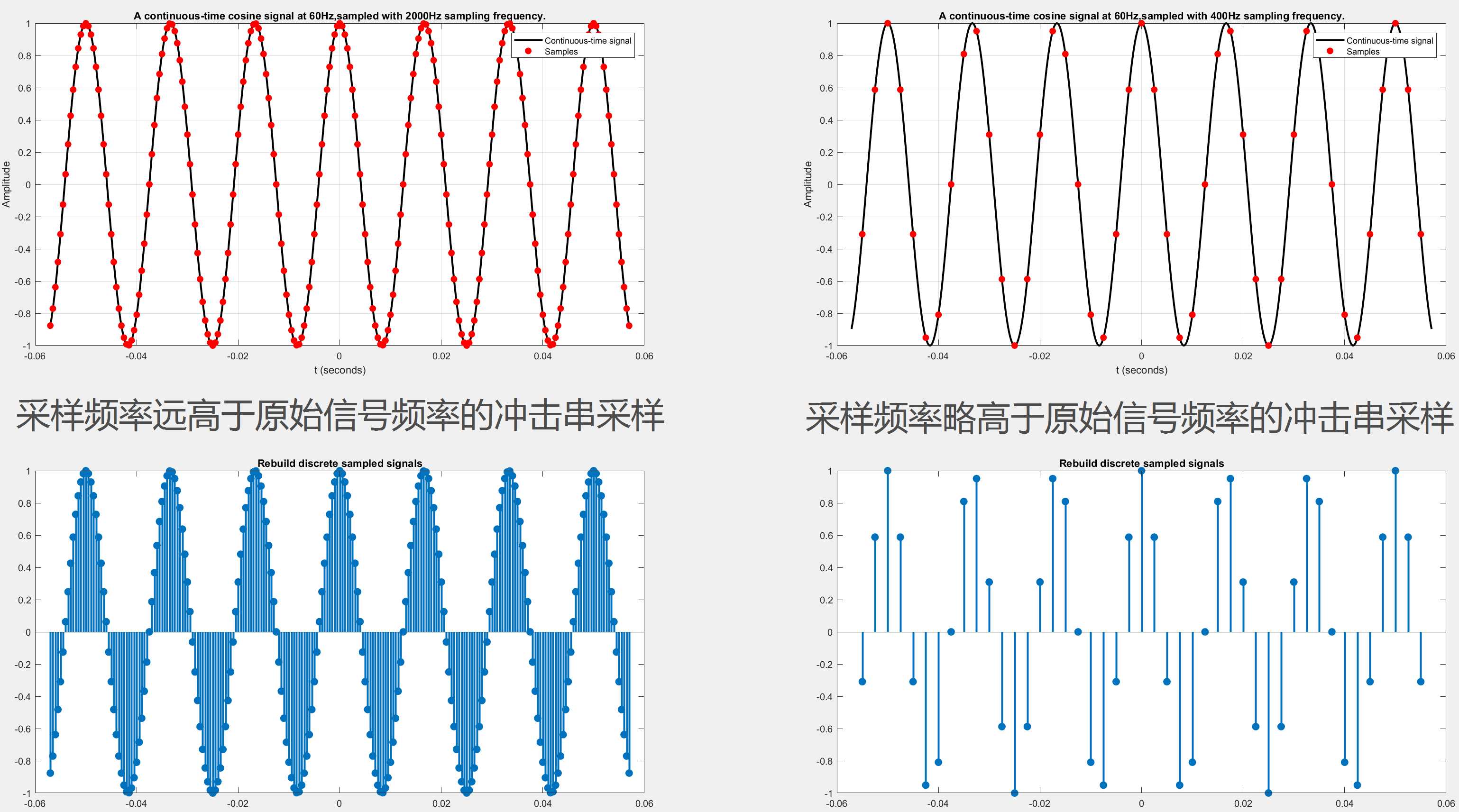
第一种情况 —— 采样频率高于原始信号频率最高频的两倍(Fs > 2*Fo)
下图所绘的是一个频率为60Hz的连续的余弦波,图中的红点为采样点。当采样冲击串的频率(2000Hz)远高于原始信号时(原始信号的33.3倍),采样点在曲线上的分布非常密集,重建后的效果也很好。如果采样频率(400Hz)只是略高于原始信号频率
(原始信号的6.6倍),则原曲线上的采样点明显不足,但不用担心,即便是这种看起来不太充足的采样还是可以重建原始的连续信号的。
点击图片放大
Matlab代码:
%% signal sampling and aliasing demo for CSDN
% Created: Late spring, 2018. (2018/05/03)
% Author: Z.Zhu, zzz0029@tigermail.auburn.edu
% Copy Rights Reserved.
% May not be copied, scanned, or duplicated, in whole or in part.
% Reference of algorithm by: Steve Eddins's Aliasing and a sampled cosine
% signal on his bolg "Steve on Image Processing"
close all;
clear all;
%% Signals with same frequency were sampled with different sampling frequencies.
Omega = 60; % freq. of continous Signal
Phi = 0; % Phase
A = 1; % Amplitude
tmin = -pi/55; % lower limit of X axis
tmax = pi/55; % uper limit of X axis
Bins = 1000; % Number of Bins
t = linspace(tmin, tmax, Bins); % Space vector
% Form a signal containing a 60(Hz) sinusoid of amplitude 1 with phase of 0.
CosineSignal = A.*cos(2.*pi.*Omega.*t + Phi);
% Plot the signal in the Space domain.
subplot(2,2,1)
plot(t,CosineSignal,'-k','LineWidth',2);
title(['A continuous-time cosine signal at ',num2str(Omega),'Hz',',sampled with 2000Hz sampling frequency.'])
ylabel('Amplitude')
xlabel('t (seconds)')
% Let's sample it with a sampling frequency of 2000Hz.
Fs = 2000; % Sampling Freq.
T = 1/Fs; % Space vector
nmin = ceil(tmin / T);
nmax = floor(tmax / T);
n = nmin:nmax;
SampleSignal2000 = A.*cos(2.*pi.*Omega.*n.*T + Phi);
hold on
plot(n*T,SampleSignal2000,'o',...
'MarkerSize',6.5,...
'MarkerEdgeColor','r',...
'MarkerFaceColor','r');
legend('Continuous-time signal','Samples','Location','northeast')
hold off
grid on
% Rebuild discrete sampled signals
subplot(2,2,3)
stem(n*T,SampleSignal2000,'filled','LineWidth',2);
title('Rebuild discrete sampled signals');
% The sampling frequency of 2000 Hz is well above 120 Hz, which is twice the frequency
% of the cosine. And you can see that the samples are clearly capturing the oscillation
% of the continuous-time cosine.
% Plot the signal in the Space domain.
subplot(2,2,2)
plot(t,CosineSignal,'-k','LineWidth',2);
title(['A continuous-time cosine signal at ',num2str(Omega),'Hz',',sampled with 400Hz sampling frequency.'])
ylabel('Amplitude')
xlabel('t (seconds)')
% Let's sample it with a sampling frequency of 400Hz.
Fs = 400; % Sampling Freq.
T = 1/Fs; % Space vector
nmin = ceil(tmin / T);
nmax = floor(tmax / T);
n = nmin:nmax;
SampleSignal400 = A.*cos(2.*pi.*Omega.*n.*T + Phi);
hold on
plot(n*T,SampleSignal400,'o',...
'MarkerSize',6.5,...
'MarkerEdgeColor','r',...
'MarkerFaceColor','r');
legend('Continuous-time signal','Samples','Location','northeast')
hold off
grid on
% Rebuild discrete sampled signals
subplot(2,2,4)
stem(n*T,SampleSignal400,'filled','LineWidth',2);
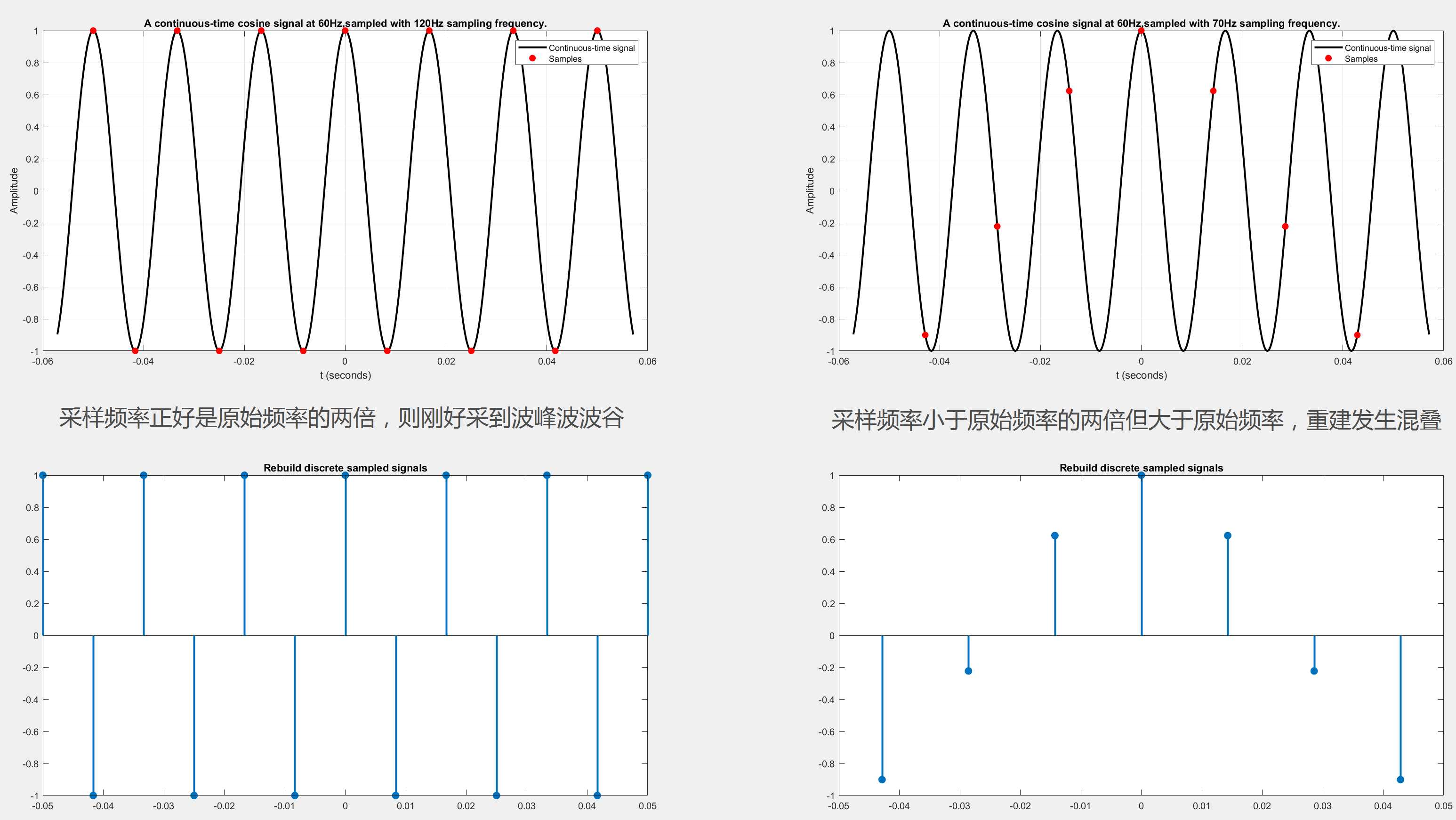
title('Rebuild discrete sampled signals');第二种情况 —— 采样频率小于原始信号频率最高频的两倍,但大于原始信号的频率(2*Fo > Fs > Fo)
下面我们逐渐降低采样率,看看会发生什么。
先是用正好两倍于原始信号频率的采样频率(120Hz)来采样(原始信号的2倍),则采到的信号,正好是余弦波的波峰或者波谷即,1和-1。(注意:我这里所使用的是相位为0的余弦波,如果相位发生改变则采集到的点,不一定正好是波峰和波谷。)
接下来,我用小于原始信号频率两倍的采样频率(70Hz)来采时(原始信号的1.16倍),采集到的信号就会发生混叠,即采集到的是一个频率低于原始信号的错误的离散信号,也无法利用该错误信号重建原始的连续信号。
点击图片放大
Matlab代码:
% Let's sample it with a sampling frequency of 120Hz.
Fs = 120; % Sampling Freq.
T = 1/Fs; % Space vector
nmin = ceil(tmin / T);
nmax = floor(tmax / T);
n = nmin:nmax;
SampleSignal120 = A.*cos(2.*pi.*Omega.*n.*T + Phi);
hold on
plot(n*T,SampleSignal120,'o',...
'MarkerSize',6.5,...
'MarkerEdgeColor','r',...
'MarkerFaceColor','r');
legend('Continuous-time signal','Samples','Location','northeast')
hold off
grid on
% Rebuild discrete sampled signals
subplot(2,2,3)
stem(n*T,SampleSignal120,'filled','LineWidth',2);
title('Rebuild discrete sampled signals');
% The samples above are still adequately capturing the shape of the cosine.Now let's drop
% the sampling frequency down to exactly 120 Hz, twice the frequency of the 60 Hz cosine.
% Plot the signal in the Space domain.
subplot(2,2,2)
plot(t,CosineSignal,'-k','LineWidth',2);
title(['A continuous-time cosine signal at ',num2str(Omega),'Hz',',sampled with 70Hz sampling frequency.'])
ylabel('Amplitude')
xlabel('t (seconds)')
% Let's sample it with a sampling frequency of 70Hz.
Fs = 70; % Sampling Freq.
T = 1/Fs; % Space vector
nmin = ceil(tmin / T);
nmax = floor(tmax / T);
n = nmin:nmax;
SampleSignal70 = A.*cos(2.*pi.*Omega.*n.*T + Phi);
hold on
plot(n*T,SampleSignal70,'o',...
'MarkerSize',6.5,...
'MarkerEdgeColor','r',...
'MarkerFaceColor','r');
legend('Continuous-time signal','Samples','Location','northeast')
hold off
grid on
% Rebuild discrete sampled signals
subplot(2,2,4)
stem(n*T,SampleSignal70,'filled','LineWidth',2);
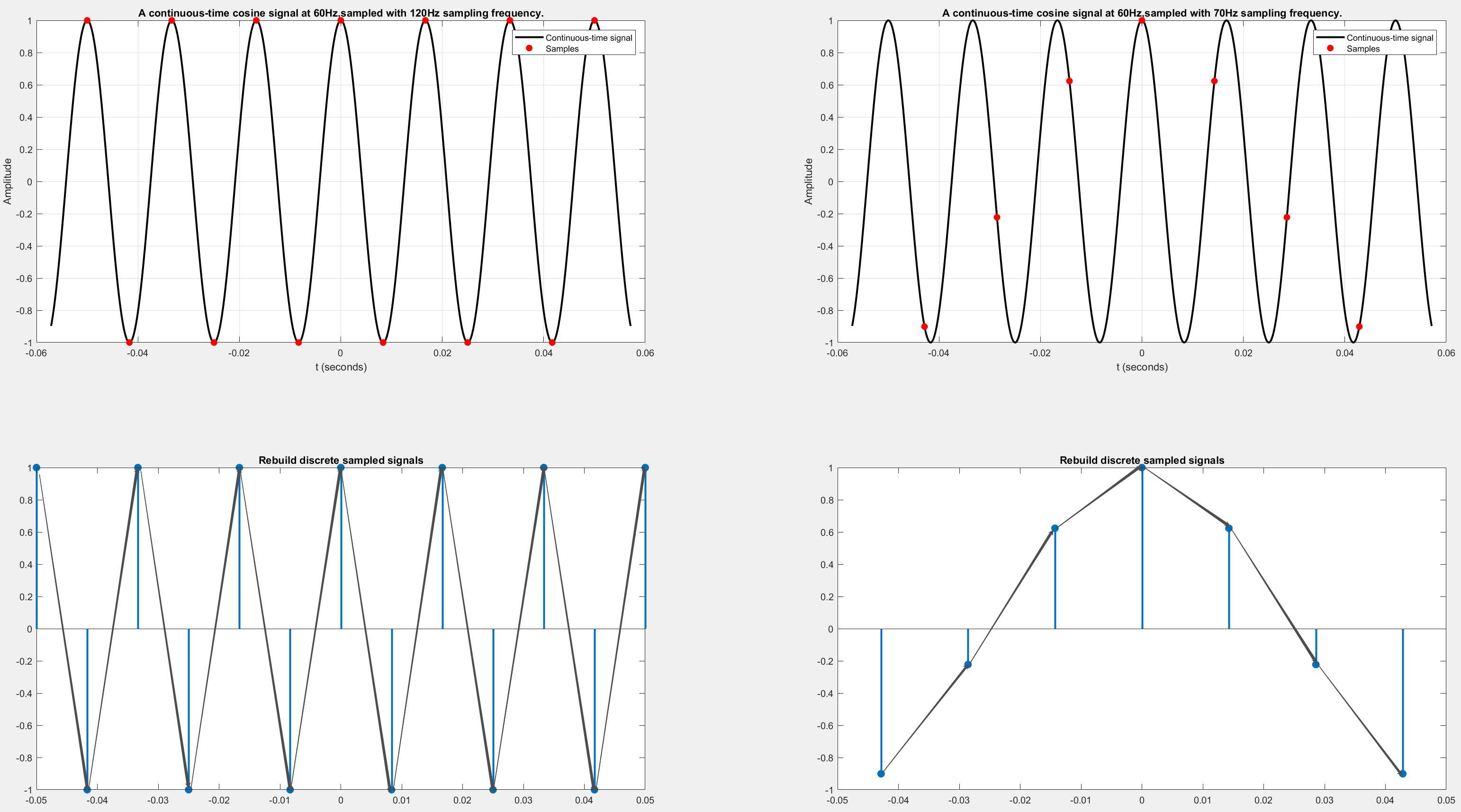
title('Rebuild discrete sampled signals');下图是利用上图中的采样点重建后的离散信号,图中我用红色的箭头大致的链接了一下图像中的离散点(真实重建的时候,不会使用直线来连接他们的,而是使用的Sinc函数。),下图的上半部分图像中的起伏和波动的频率和原始信号是相同的,而下半部分的图像的波动就明显慢了很多。
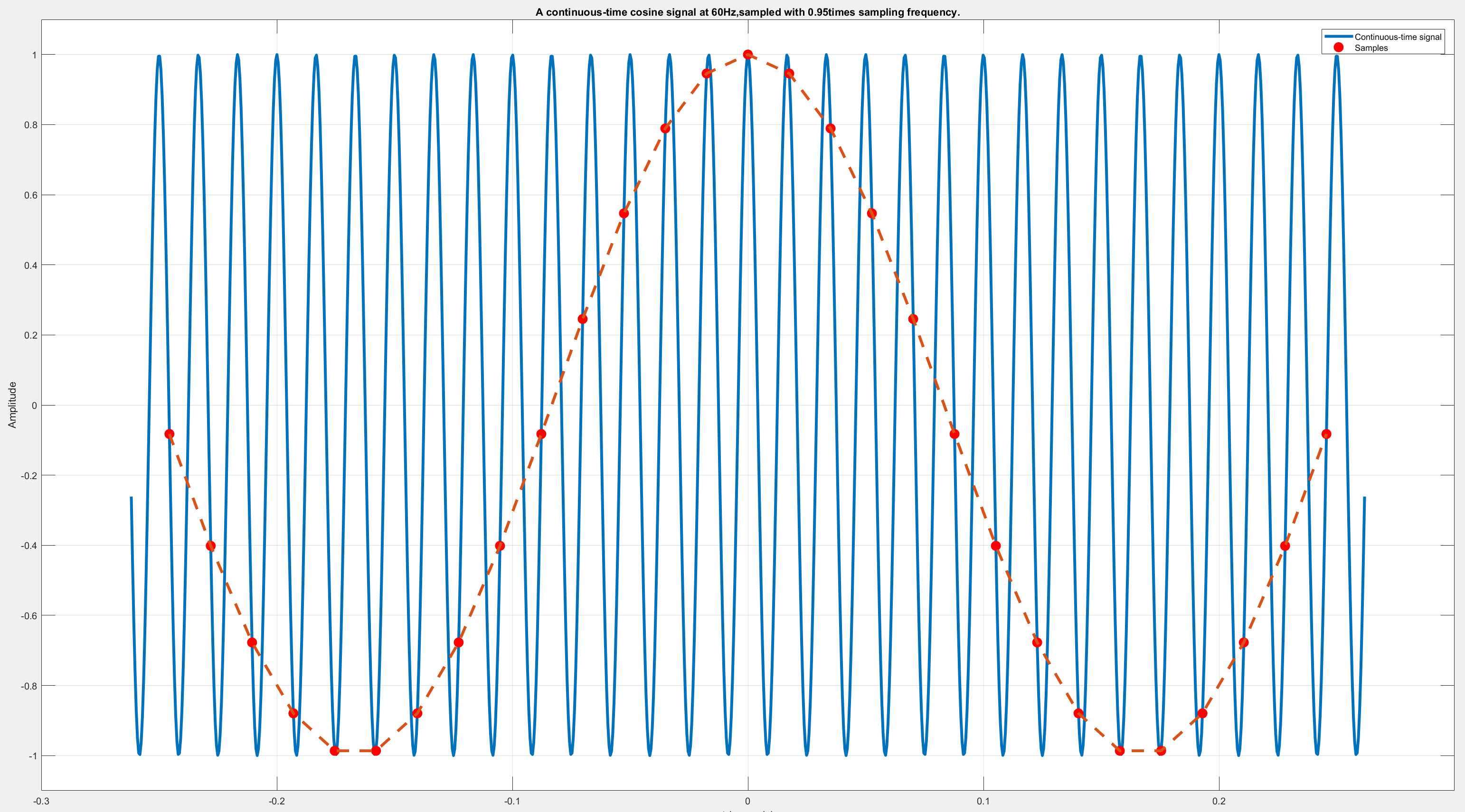
第三种情况 —— 采样频率小于原始信号的频率( Fs < Fo)
最后,当我用一个小于原始信号频率的采样信号去采样时(原始信号的0.95倍),得到了一个非常明显的“低频”信号。下图中红色的虚线是采样点的包络,很明显他要比图中快速起伏的蓝色曲线慢了很多。
点击图片放大
Matlab代码:
% Plot the signal with a wider range.
figure;
plot(t,CosineSignal,'LineWidth',3);
title(['A continuous-time cosine signal at ',num2str(Omega),'Hz',',sampled with 0.95times sampling frequency.'])
ylabel('Amplitude')
xlabel('t (seconds)')
Fs = 0.95*Omega; % Sampling Freq.
T = 1/Fs; % Space vector
nmin = ceil(tmin / T);
nmax = floor(tmax / T);
n = nmin:nmax;
SampleSignal = A.*cos(2.*pi.*Omega.*n.*T + Phi);
hold on
plot(n*T,SampleSignal,'ro', 'MarkerSize',10, 'MarkerFaceColor','r');
plot(n*T,SampleSignal,'--','LineWidth',3);
legend('Continuous-time signal','Samples','Location','northeast')
axis([ -0.3 0.3 -1.1 1.1])
hold off
grid on奈奎斯特采样定理:
上面的实验揭示了采样率Fs和所测信号频率Fo之间的关系。 只有采样率Fs必须大于被测信号最高频率Fo的两倍(采样率的一半通常被称为奈奎斯特频率Fn)才不会发生混叠,这就是著名的奈奎斯特采样定理。
Tips : 这里的录像说明和上面的MATLAB仿真一个很大的不同。这里的仿真是保持采样频率Fs不变,不断地改变原始信号的频率Fo.
举例:大家注意去看那个老式的电风扇,或者是汽车的轮子.你调1档的时候你是可以分辨出风扇的旋转速度,旋转方向的。到了二档,就有些费力了。到了三挡,你就会发现风扇还是有风,可是好像停住不转了。到了四档你又看见,风扇开始倒转了,而且倒转的速度很慢。
这也就是说高频信息和低频信息混合在一起了,扑所迷离,晦暗莫测,百转千回,让人难以捉摸(说明高转速风扇的奈奎斯特频率高于人眼所能企及的采样频率。)!
“天之苍苍,其正色耶?其远而无法至极耶?”
80年代MIT录像带教程大放送:
下面截取了我最喜欢的一个教学视频中的一小段来说明信号的采样与混叠。这是我好不容易找到又花了好多时间转出来的,还望大家不要COPY。谢谢!
整个实验要做的就是保持采样频率Fs不变,不断地增加原始信号cos(Fo*t)的频率Fo,最终必然会导致采样不足,即而出现混叠!
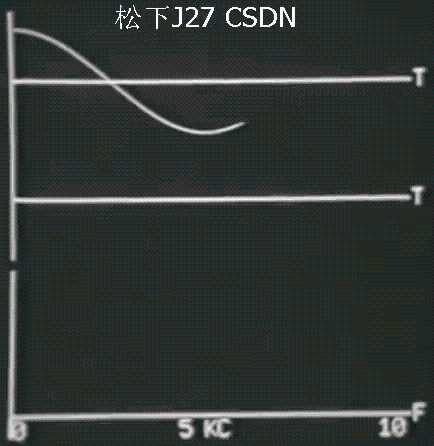
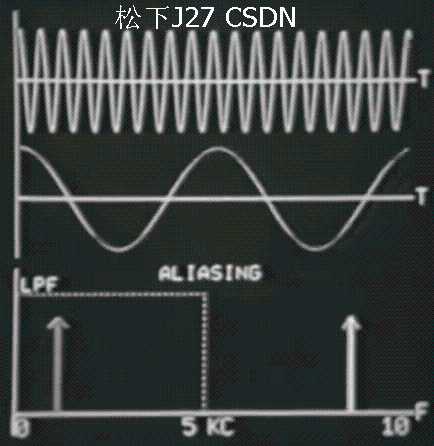
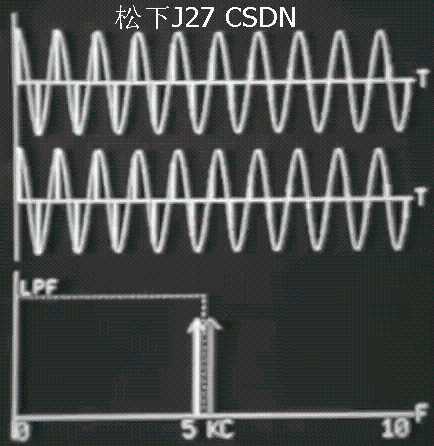
Continuous signal Part I 输入信号及其傅里叶频率
图中第一行是输入信号,第二行是准备重建的信号,第三行是驶入信号的频谱。由于频率是周期的所以下图中在10Hz附近出现了一个对称的频段。
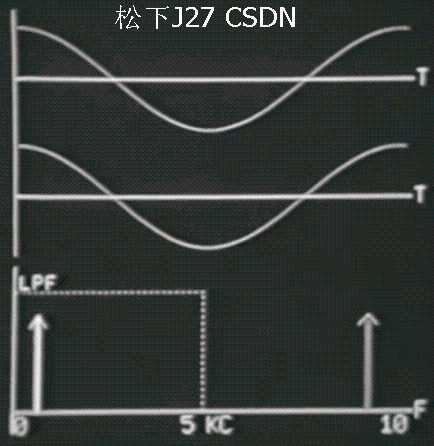
下面用CUTOFF频率(Fc)为5Hz的低通滤波器来重建信号,采样频率(Fs)则是截止频率的两倍,即 Fs = 2*Fc = 10Hz 。这时大家看到的是上面我说的第一种情况(没有混叠),即,输入信号频率的频率(肯定小于截止频率5Hz)小于采样频率(10Hz)的一半。(Fo < Fs/2)
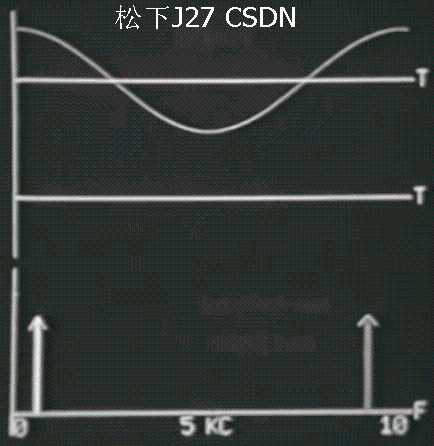
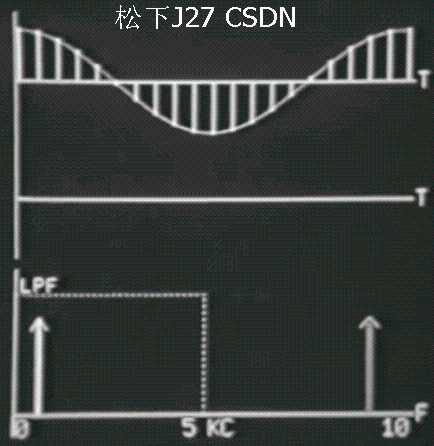
Continuous signal Part II 输入信号的重建
Continuous signal Part III 输入信号采样充分,完美复现冲入信号
下面不断的增加原始信号的频率Fo,频谱图中的冲击不断地往高频移动。重建的信号和输入信号一模一样,完美重建!请注意刚好出现混叠那个地方的临界状况。
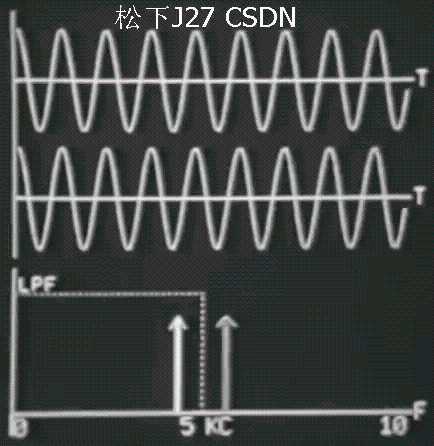
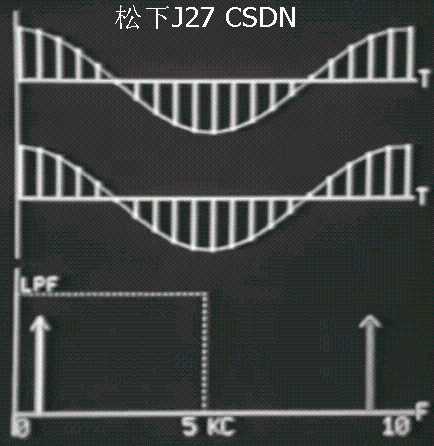
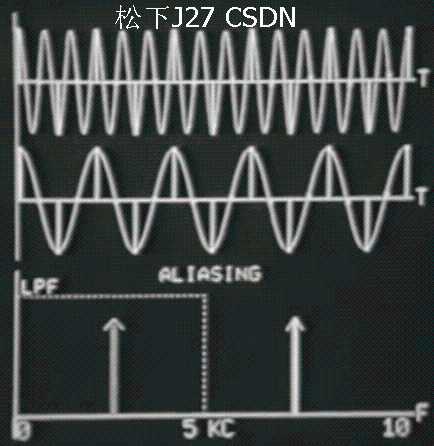
Continuous signal Part IV 输入信号采样不足,发生混叠,重建信号有误
继续增加输入信号的频率Fo直到原始频率大于采样频率的一半(即截止频率5Hz)。这就是我在上面所提到的第二种情况和第三种情况,输入信号的频率大于截止频率Fo >Fc(其中Fc=Fs/2)。重建信号的频率明显要小于输入信号的频率,而且随着输入信号的频率越来越高(第一行信号),重建后的混叠信号(第二行信号)的频率越来越低。
Continuous signal Part V 混叠信号的回滚
逐渐降低信号的频率,混叠最终消失,信号最终被完美重建。
下面我再展示一下离散信号的录像。(由于上传图像最大不能超过10M,所以我这里分批上传,还望见谅。)
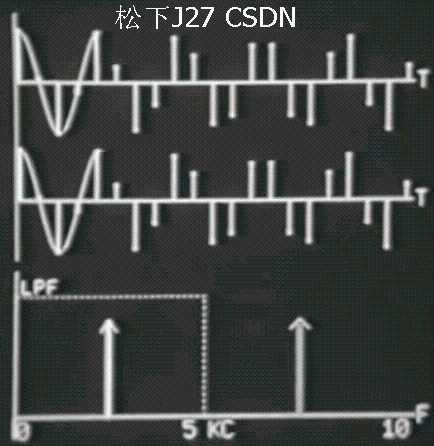
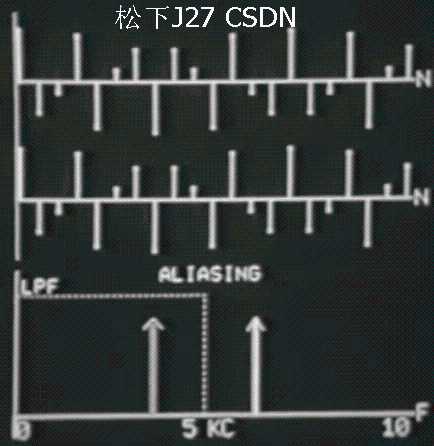
Discrete signal Part I 无混叠部分
Discrete signal Part II 混叠部分
混叠是需要避免的,可在采样之前使用抗混叠滤波器。如若已经发生了混叠,那么混叠后的那个“伪装信号”在哪?他的频率又是多少呢?这一系列的第二讲我来给大家说说。
(全文完)
作者 — 松下J27
谢谢收看,下次再见!
鸣谢:
【1】Matlab博客里面的 Steve先生,以及他的博文:
【2】https://blogs.mathworks.com/steve/2010/03/03/aliasing-and-a-sampled-cosine-signal/?s_tid=srchtitle
【3】奥本海姆主讲的MIT open course, signal and system.
《圣经》希伯来书13章8节 耶稣基督昨日今日一直到永远,是一样的。
*配图和本文无关(图为:扫罗的悔改)*
版权声明:所有的笔记,可能来自很多不同的网站和说明,在此没法一一列出,如有侵权,请告知,立即删除。欢迎大家转载,但是,如果有人引用或者COPY我的文章,必须在你的文章中注明你所使用的图片或者文字来自于我的文章,否则,侵权必究。 —-松下J27
今天的文章数字信号处理 — 信号的采样和奇妙的混叠(Aliasing) 壹分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/26788.html