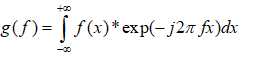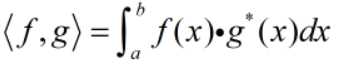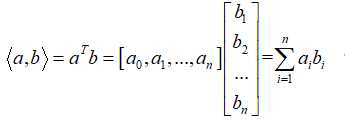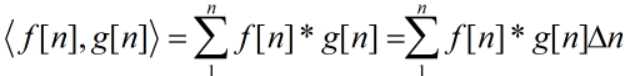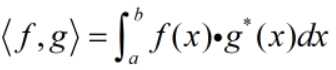小谈向量内积与函数内积

这是我的第一篇原创博客，谈谈自己在读研中的一些小思考，希望能给大家的学习带来一点启发。

对于函数内积，我想很多理工科的都理解，最常用的就是傅里叶变换，一个信号与很多个频率的基函数相乘，也就是信号与每个基函数做内积，求得在每个基函数上的占比，或者说是在该基函数上的投影大小，遍历全部基函数，就求得在全部基函数的占比。

而函数内积的定义为：

可能很多人会想为什么函数也可以有内积，为什么这样定义，它跟一般的向量内积又有什么联系呢？

回顾一下两个向量的内积：

我们直到两个向量的内积可以看作是a向量投影到b向量，也可以看作是b向量投影到a向量；如果两个向量正交，那他们的内积就为零。某种意义上，可见向量内积也可以看作是两者相似程度的度量。

回到函数的内积，若两个函数是离散的，即f[n],g[n],我们不就可以把该函数看作是一个在n维空间展开的向量

可见一个离散函数的内积下形式是跟一般向量内积的形式是一致的。
如果我们把离散的函数变成连续的，只不过是把求和函数变成积分，delta_n 变成dx。

即可得到

如果是复函数，乘上自身共轭即可。

本人才疏学浅，若有错误，欢迎交流指出
码字不易，喜欢的话，点个赞吧

今天的文章小谈向量内积与函数内积分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。