线性判别分析(LDA)降维

一、什么是线性判别分析？

线性判别分析(Linear discriminant Analysis，LDA)与PCA类似也是一种特征抽取的算法，它能够提高数据分析过程中的计算效率。PCA是寻找数据集中方差最大的方向作为主成分分量的轴，而LDA是最优化分类的特征子空间。LDA和PCA都是用来降低数据维度的线性转换技巧。PCA属于无监督算法，LDA属于监督算法。相对于PCA算法而言，LDA更适合对于分类特征的提取。

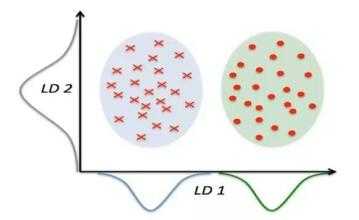
上图中，叉叉表示类别1，实心圆表示类别2，LD1表示x轴，LD2表示y轴。其中，类别1和类别2都满足正态分布，我们对类别1和类别2分布在x轴和y轴上进行投影，在x轴方向上，通过线性判定，我们可以将类别1和类别2区分开，所以它是一个好的线性判定。而y轴方向的线性判定保持了数据集的较大方差，而无法将类别1和类别2进行区分，所以它不是一个好的线性判定。

二、如何来做线性判别分析？

在使用线性判别分析之前，还需要满足几个假设条件。第一个假设是数据需要满足正态分布，第二个就是各个类别数据具有相同的协方差矩阵，且样本的特征是相互独立的。即使没有满足这些条件，LDA还是可以很好的工作，LDA一共包含了6个步骤：

1、标准化处理

import pandas as pd
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split

if __name__ ==

今天的文章线性判别分析(LDA)降维分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。