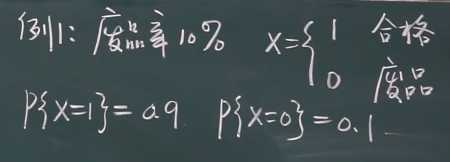一、0-1分布

0-1分布是指一件事情，要么发生，要么不发生，发生的概率是p，不发生的概率则是1-p；
或者说一件事物，要么是状态1、要么是状态0，状态1的概率是p，状态0的概率则是1-p。
$\begin{array}{ccc}X& 1& 0\\ P& p& 1-p\end{array}$

0-1分布概率为：

P { X = k } = p k ( 1 − p ) 1 − k ， 其 中 k = { 0 , 1 } P\{X=k\}=p^k(1-p)^{1-k}，其中k=\{0,1\} P{
X=k}=pk(1−p)1−k，其中k={
0,1}

例：

比如说根据大量样品统计计算出，生产出一件产品，合格的概率是0.9，是废品的概率是0.1。
那么
P { X = 1 } = 0. 9 1 ( 1 − 0.9 ) 1 − 1 = 0.9 P\{X=1\}=0.9^1(1-0.9)^{1-1}=0.9 P{
X=1}=0.91(1−0.9)1−1=0.9 P { X = 0 } = 0. 9 0 ( 1 − 0.9 ) 1 − 0 = 0.1 P\{X=0\}=0.9^0(1-0.9)^{1-0}=0.1 P{
X=0}=0.90(1−0.9)1−0=0.1

二、几何分布

事件发生的概率为 $p$ ，前 $k-1$ 次不发生，第 $k$ 次发生的概率为：
P { X = k } = ( 1 − p ) k − 1 × p ， 其 中 k = 1 , 2 , 3… P\{X=k\}=(1-p)^{k-1}\times p，其中k=1,2,3… P{
X=k}=(1−p)k−1×p，其中k=1,2,3...

例如：射击中，射中的概率为0.6，连续射击4次没中，第5次才射中的概率为
P { X = 5 } = ( 1 − 0.6 ) 5 − 1 × 0.6 = 0. 4 4 × 0.6 = 0.01536 P\{X=5\}=(1-0.6)^{5-1}\times 0.6=0.4^4\times 0.6=0.01536 P{
X=5}=(1−0.6)5−1×0.6=0.44×0.6=0.01536

三、二项分布

事件发生的概率为 $p$ ，做了 $n$ 次实验，发生了 $k$ 次的概率：
P { X = k } = C n k p k ( 1 − p ) n − k ， 其 中 k = 0 , 1 , 2 , 3… n P\{X=k\} = C_n^kp^k(1-p)^{n-k}，其中k=0,1,2,3…n P{
X=k}=Cnk​pk(1−p)n−k，其中k=0,1,2,3...n
记为：
$$X\sim B(n,p)$$
0-1分布是二项式分布特例，此时$n=1,k=0,1$

四、泊松分布

日常生活中，大量事件是有固定频率的。

• 某医院平均每小时出生3个婴儿
• 某公司平均每10分钟接到1个电话
• 某超市平均每天销售4包xx牌奶粉
• 某网站平均每分钟有2次访问

它们的特点就是，我们可以预估这些事件的总数，但是没法知道具体的发生时间。已知平均每小时出生3个婴儿，请问下一个小时，会出生几个？

有可能一下子出生6个，也有可能一个都不出生。这是我们没法知道的。泊松分布就是描述某段时间内，事件具体的发生概率。

泊松分布是二项分布的极限情况，n是无穷大的
P { X = k } = lim ⁡ n → ∞ C n k × p k × ( 1 − p ) n − k = λ k k ! e − λ \begin{aligned} P\{X=k\}=&\lim_{n→∞} C_{n}^{k}\times p^{k}\times (1-p)^{n-k} \\ =&\frac{λ^{k}}{k!}e^{-λ} \end{aligned} P{
X=k}==​n→∞lim​Cnk​×pk×(1−p)n−kk!λk​e−λ​
记为：
$$X\sim P(\lambda )$$

上面就是泊松分布的公式。等号的左边，P 表示概率，k 表示数量，λ 表示事件的频率，此处等于3。

接下来两个小时(此处λ=3*2=6)，一个婴儿都不出生的概率是：
P { X = 0 } = 6 0 0 ! e − 6 ≈ 0.0025 P\{X=0\}=\frac{6^{0}}{0!}e^{-6}\approx 0.0025 P{
X=0}=0!60​e−6≈0.0025

接下来一个小时(此处λ=3)，至少出生两个婴儿的概率是：
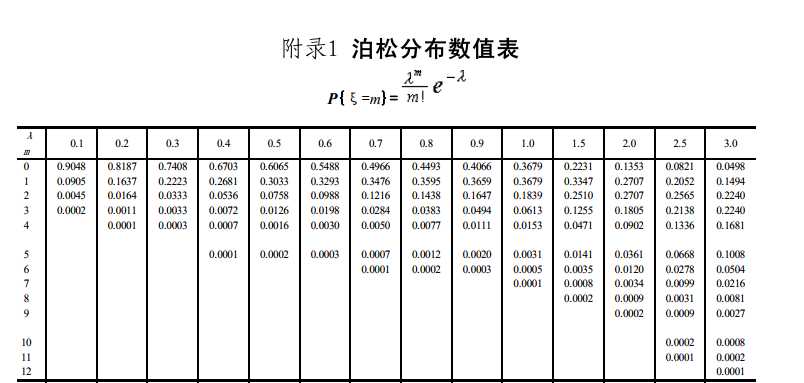
P { X ≥ 2 } = 1 − P { X < 2 } = 1 − P { X = 1 } − P { X = 0 } = 1 − 3 1 1 ! e − 3 − 3 0 0 ! e − 3 ≈ 1 − 0.1494 − 0.0498  (查表) ≈ 0.8009 \begin{aligned} P\{X\ge2\} =&1-P\{X\lt2\}\\ =&1-P\{X=1\}-P\{X=0\}\\ =&1-\frac{3^{1}}{1!}e^{-3}-\frac{3^{0}}{0!}e^{-3}\\ \approx&1-0.1494-0.0498 ~\text{(查表)} \\ \approx& 0.8009 \end{aligned} P{
X≥2}===≈≈​1−P{
X<2}1−P{
X=1}−P{
X=0}1−1!31​e−3−0!30​e−31−0.1494−0.0498 (查表)0.8009​

例1（摘自《泊松分布与美国枪击案》）：
已知某家小杂货店，平均每周售出2个水果罐头。请问该店水果罐头的最佳库存量是多少？

各个参数的含义：
P：每周销售k个罐头的概率。
X：水果罐头的销售变量。
k：X的取值（0，1，2，3…）。
λ：每周水果罐头的平均销售量2。
　
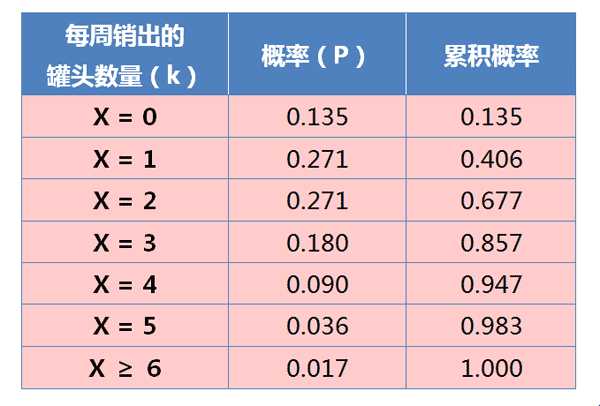
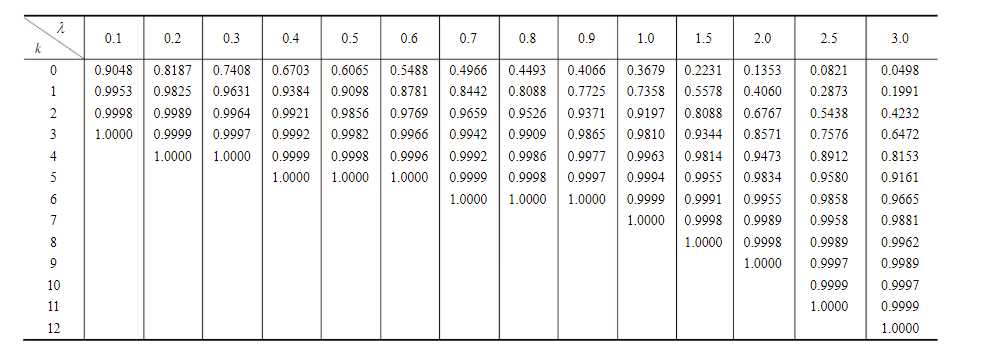
从上表可见，如果存货4个罐头，95%的概率不会缺货（平均每19周发生一次）；如果存货5个罐头，98%的概率不会缺货（平均59周发生一次）。

例2（摘自视频）：
电话台平均每分钟接到3次电话，符合泊松分布$X\sim P(3)，\lambda =3$，问每分钟接到电话不超过5次的概率？
解：
P { X = k } = λ k k ! e − λ = 3 k k ! e − 3 P\{X=k\}=\cfrac{λ^{k}}{k!}e^{-λ}=\cfrac{3^{k}}{k!}e^{-3} P{
X=k}=k!λk​e−λ=k!3k​e−3
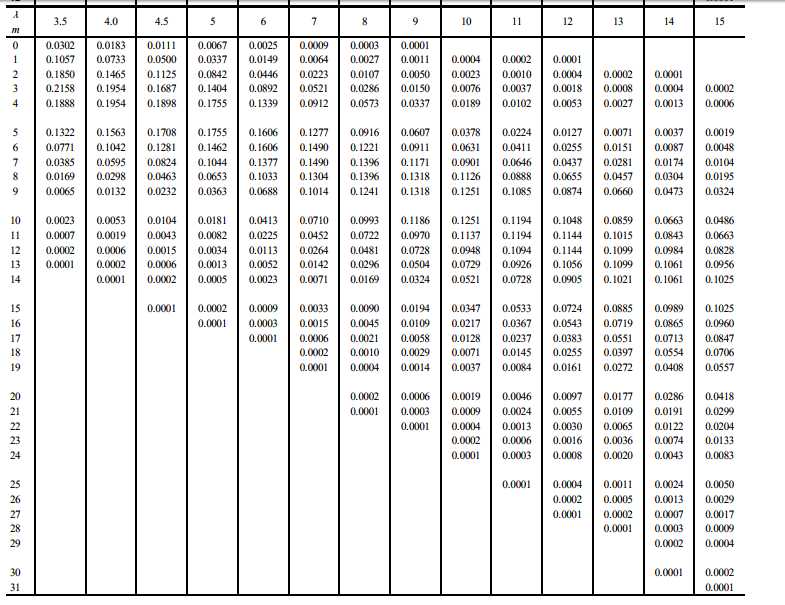
P { X ≤ 5 } = ∑ k = 0 5 3 k k ! e − 3 = 0.916 P\{X\leq5\}=\displaystyle\sum_{k=0}^5\cfrac{3^{k}}{k!}e^{-3}=0.916 P{
X≤5}=k=0∑5​k!3k​e−3=0.916 (查表)
网上有泊松分布累加表与数值表两种，后者需要累加起来，如下是累加表：

泊松分布数值表：

参考资料：
《泊松分布与美国枪击案》
《泊松分布和指数分布：10分钟教程》
《如何通俗理解泊松分布？》
《概率论与数理统计》教学视频全集（宋浩）泊松分布
《泊松分布函数表》

五、超几何分布

如下图所示，总共100个学生，男生60人，女生40人，取10个学生，问取的10人中男生人数为k的概率是多少？

总共有$C_{100}^{10}种情况$，取k个男生的情况有$C_{60}^k{C}_{40}^{10-k}$种，概率为：
P { X = k } = C 60 k C 40 10 − k C 100 10 ， 其 中 k = 0 , 1 , 2… , 10 P\{X=k\}=\cfrac{C_{60}^kC_{40}^{10-k}}{C_{100}^{10}}，其中k=0,1,2…,10 P{
X=k}=C10010​C60k​C4010−k​​，其中k=0,1,2...,10

参考资料：
《概率论与数理统计》教学视频全集（宋浩）超几何分布

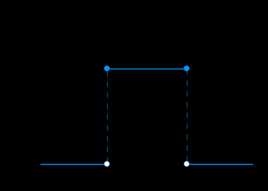
六、均匀分布

均匀分布也叫矩形分布，它是对称概率分布，在相同长度间隔的分布概率是等可能的。
均匀分布的概率密度函数为：
$$f(x)=\{\begin{array}{ll}\frac{1}{b-a}& a\le x\le b\\ 0& \text{else}\end{array}$$
X服从均匀分布记为：
$$X\sim U[a,b]$$

如下图所示，$\frac{1}{b-a}\times (b-a)=1$，即是$f(x)$的积分面积，即总概率之和为1：

分布函数为
$$f(x)=\{\begin{array}{ll}0& x<a\\ \frac{x-a}{b-a}& a\le x<b\\ 1& x\ge b\end{array}$$

七、指数分布

参考四、泊松分布
指数分布是事件的时间间隔的概率。下面这些都属于指数分布。

• 婴儿出生的时间间隔
• 来电的时间间隔
• 奶粉销售的时间间隔
• 网站访问的时间间隔

指数分布密度函数：
$$f(x)=\{\begin{array}{ll}\lambda e^{-\lambda x}& x>0\\ 0& x\le 0\end{array}$$
分布函数：
$$f(x)=\{\begin{array}{ll}1-e^{-\lambda t}& x>0\\ 0& x\le 0\end{array}$$
X服从指数分布，记为：
$$X\sim \exp (\lambda )$$

指数分布的公式可以从泊松分布推断出来。如果下一个婴儿要间隔时间 t ，就等同于 t 之内没有任何婴儿出生。
P { X > t } = P { X = 0 } = ( λ t ) k k ! e − λ t = ( λ t ) 0 0 ! e − λ t = e − λ t \begin{aligned} P\{X>t\} &=P\{X=0\}\\ &=\cfrac{(λt)^{k}}{k!}e^{-λt}\\ &=\cfrac{(λt)^{0}}{0!}e^{-λt}\\ &=e^{-λt} \end{aligned} P{
X>t}​=P{
X=0}=k!(λt)k​e−λt=0!(λt)0​e−λt=e−λt​

反过来，事件在时间 t 之内发生的概率，就是1减去上面的值。
P { X ≤ t } = 1 − P { X > t } = 1 − e − λ t P\{X\le t\}=1-P\{X>t\}=1-e^{-λt} P{
X≤t}=1−P{
X>t}=1−e−λt
接下来15分钟，会有婴儿出生的概率为：
P { X ≤ 0.25 } = 1 − e − 3 × 0.25 ≈ 0.5276 P\{X\le 0.25\}=1-e^{-3\times0.25}\approx0.5276 P{
X≤0.25}=1−e−3×0.25≈0.5276
接下来的15分钟到30分钟，会有婴儿出生的概率是：
P { 0.25 ≤ X ≤ 0.5 } = P { X ≤ 0.5 } − P { X ≤ 0.25 } P\{0.25\le X\le 0.5\}=P\{X\le 0.5\}-P\{X\le 0.25\} P{
0.25≤X≤0.5}=P{
X≤0.5}−P{
X≤0.25}
参考资料：
《泊松分布和指数分布：10分钟教程》
《概率论与数理统计》教学视频全集（宋浩）指数分布

八、正态分布

正态曲线呈钟型，两头低，中间高，关于直线 $x=\mu$ 对称，并在$x=\mu$处取得最大值$\frac{1}{\sigma \sqrt{2\pi }}$，因其曲线呈钟形，因此人们又经常称之为钟形曲线。

若随机变量X服从一个数学期望为$\mu$、方差为${\sigma }^2$的正态分布，记为：
$$X\sim N(\mu ,{\sigma }^2)$$

方差公式： ${\sigma }^2=\frac{\sum _{i=1}^N(x_i-\mu {)}^2}{N}$
标准差公式：$\sigma =\sqrt{{\sigma }^2}$

期望值μ决定曲线的左右位置，标准差σ决定分布的幅度。μ不变，σ值越小越陡峭。

正态分布的密度函数为：$$\varphi (x)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{1}{2}(\frac{x-\mu }{\sigma }{)}^2}$$

当 $\mu =0,\sigma =1$ 时的正态分布是标准正态分布，记为$X\sim N(0,1)$。标准正态分布可以查表求值。

查考资料：
《百度百科-正态分布》
《数学乐-正态分布》
《标准正态分布表》
《概率论与数理统计》教学视频全集（宋浩）正态分布
《正态分布（高斯分布）》

今天的文章八种概率分布模型分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。