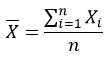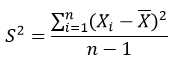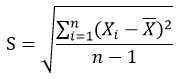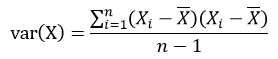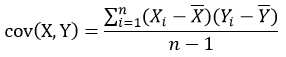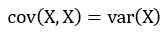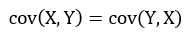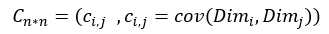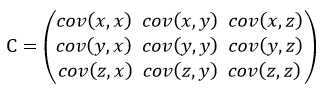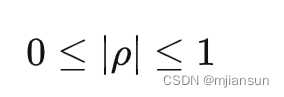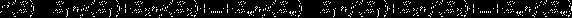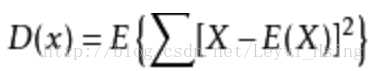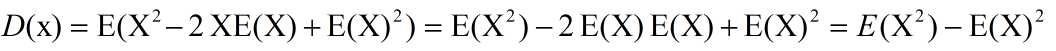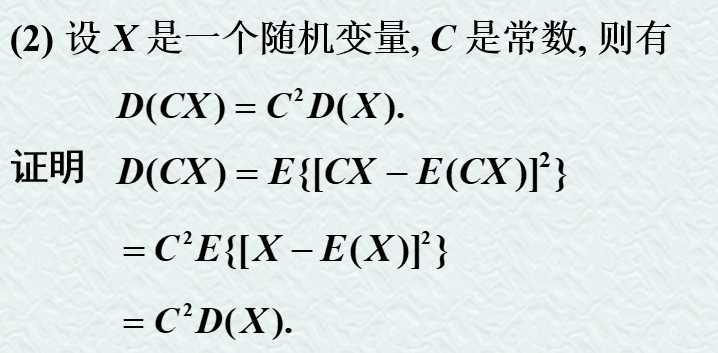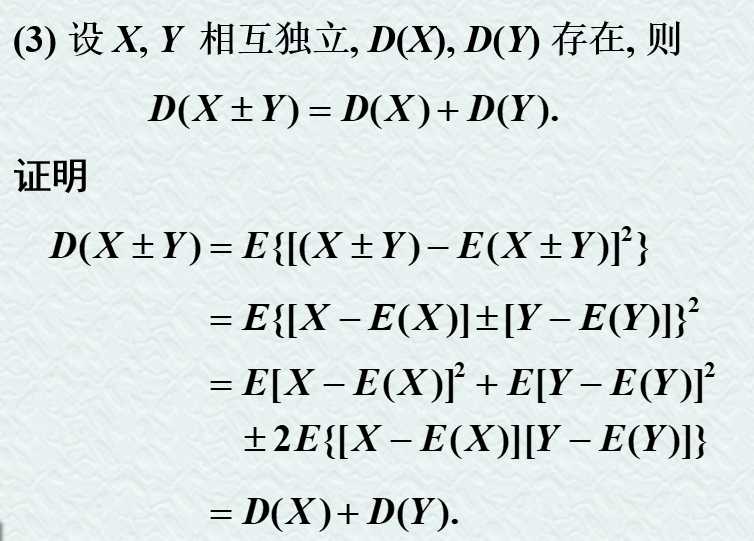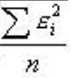1. 写在前面

平均值，标准差，方差，协方差都属于统计数学；期望属于概率数学。

2. 统计数学

2.1 平均值，标准差，方差

统计学里最基本的概念就是样本的均值、方差、标准差。首先，我们给定一个含有n个样本的集合，下面给出这些概念的公式描述：

均值：

方差：

标准差：

均值描述的是样本集合的中间点，它告诉我们的信息是有限的。

方差（variance)是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。统计中的方差（样本方差）是各个数据分别与其平均数之差的平方的和的平均数。在许多实际问题中，研究方差即偏离程度有着重要意义。方差是衡量源数据和期望值相差的度量值。

而标准差给我们描述的是样本集合的各个样本点到均值的距离之平均。

以这两个集合为例，[0, 8, 12, 20]和[8, 9, 11, 12]，两个集合的均值都是10，但显然两个集合的差别是很大的，计算两者的标准差，前者是8.3后者是1.8，显然后者较为集中，故其标准差小一些，标准差描述的就是这种“散布度”。之所以除以n-1而不是n，是因为这样能使我们以较小的样本集更好地逼近总体的标准差，即统计上所谓的“无偏估计”。而方差则仅仅是标准差的平方。

方差和标准差的区别：

方差与我们要处理的数据的量纲是不一致的，多了个平方，虽然能很好的描述数据与均值的偏离程度，但是处理结果是不符合我们的直观思维的。 而标准差的根号就抵消了这个平方，就能相对直观了描述数据与均值之间的偏离程度。

2.2 协方差

标准差和方差一般是用来描述一维数据的，但现实生活中我们常常会遇到含有多维数据的数据集，最简单的是大家上学时免不了要统计多个学科的考试成绩。面对这样的数据集，我们当然可以按照每一维独立的计算其方差，但是通常我们还想了解更多，比如，一个男孩子的猥琐程度跟他受女孩子的欢迎程度是否存在一些联系。协方差就是这样一种用来度量两个随机变量关系的统计量，我们可以仿照方差的定义：

来度量各个维度偏离其均值的程度，协方差可以这样来定义：

协方差的结果有什么意义呢？如果结果为正值，则说明两者是正相关的（从协方差可以引出“相关系数”的定义），也就是说一个人越猥琐越受女孩欢迎。如果结果为负值， 就说明两者是负相关，越猥琐女孩子越讨厌。如果为0，则两者之间没有关系，猥琐不猥琐和女孩子喜不喜欢之间没有关联，就是统计上说的“相互独立”。

从协方差的定义上我们也可以看出一些显而易见的性质，如：

2.3 协方差矩阵

前面提到的猥琐和受欢迎的问题是典型的二维问题，而协方差也只能处理二维问题，那维数多了自然就需要计算多个协方差，比如n维的数据集就需要计算个协方差，那自然而然我们会想到使用矩阵来组织这些数据。给出协方差矩阵的定义：

这个定义还是很容易理解的，我们可以举一个三维的例子，假设数据集有三个维度，则协方差矩阵为：

可见，协方差矩阵是一个对称的矩阵，而且对角线是各个维度的方差。

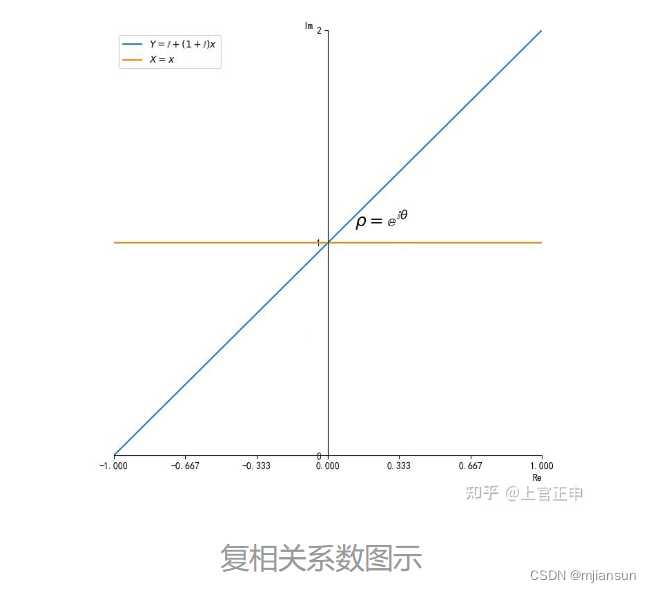
2.4 相关系数以及复相关系数的几何意义

很显然，协方差表示两个变量的观测值对均值的偏离构成的向量的内积。两个向量的夹角越小，说明两个变量越是正相关，两个向量夹角越大，说明两个变量越是负相关。其实两个向量的夹角的余弦值就是相关系数

 显然

3. 概率论

3.1 期望（相当于统计数学中的均值）

离散型

离散型随机变量X的取值为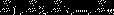，为X对应取值的概率，可理解为数据出现的频率，则：

连续型

3.2 方差

E(X)表示期望，X表示原始数据，其结果就为方差。当方差很小时，X的值形成的簇比较接近它们的期望值。方差的平方根被称为标准差(standard deviation)。D(X)还可以简化为：

 这里我是这么理解的：E的作用就是求平均，既然求完平均了，那么E(X)不就是一个常数了嘛，既然是常数了，拿平均自己那还是自己呀，也就是E(E(X))那不就是E(X)嘛。既然是这样那就好理解了，E(2XE(X))=2E(X)E(X)，E(X)的平方那也是常数，求平均还是自己。

另外再看一个例子：

3.3 标准差

方差的平方根被称为标准差(standard deviation)。简单来说，标准差是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准差，代表大部分的数值和其平均值之间差异较大；一个较小的标准差，代表这些数值较接近平均值。

这里标准差和方差的区别与统计学中一样。

4. 均方误差

均方误差一般被用在机器学习的预测值与真实值之间的距离。

标准差（Standard Deviation），中文环境中又常称均方差，但不同于均方误差（mean squared error，均方误差是各数据偏离真实值的距离平方和的平均数，也即误差平方和的平均数，计算公式形式上接近方差，它的开方叫均方根误差，均方根误差才和标准差形式上接近），标准差是离均差平方和平均后的方根，用σ表示。标准差是方差的算术平方根。 
从上面定义我们可以得到以下几点： 
1、均方差就是标准差，标准差就是均方差 
2、均方误差不同于均方差 
3、均方误差是各数据偏离真实值的距离平方和的平均数 
举个例子：我们要测量房间里的温度，很遗憾我们的温度计精度不高，所以就需要测量5次，得到一组数据[x1,x2,x3,x4,x5],假设温度的真实值是x，数据与真实值的误差e=x-xi 
那么均方误差MSE= 
总的来说，均方差是数据序列与均值的关系，而均方误差是数据序列与真实值之间的关系，所以我们只需要搞清楚真实值和均值之间的关系就行了。

参考

 全网独家讲透“协方差”与“相关系数”，成数学高手！ – 知乎

今天的文章平均值，标准差，方差，协方差，期望，均方误差分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。