层次聚类(Hierarchical Clustering)——BIRCH算法详解及举例

1 BIRCH概述

BIRCH（Balanced Iterative Reducing and Clustering Using Hierarchies）的主要动机是两个方面，一是处理大数据集，二是对异常值的鲁棒性。该算法中引入两个概念：聚类特征（Clustering　Feature，CF）和聚类特征树（CF-tree），通过这两个概念对簇进行概括，利用各个簇之间的距离，采用层次方法的平衡迭代对数据集进行规约和聚类。

2 聚类特征（CF）

CF是BIRCH增量聚类算法的核心，使用CF概括描述各簇的信息，设某簇中有N个D维数据点 { x → n } ( n = 1 , 2 , . . . , N ) \{\overrightarrow x_n\}(n=1,2,…,N) {
x
n​}(n=1,2,...,N),则该簇的聚类特征定义为三元组：
$$CF=(N,LS,SS)$$
其中N是簇中点的数目，矢量LS是个各点的线性求和即${\sum }_{n=1}^N{\overrightarrow{x}}_n=({\sum }_{n=1}^N{x}_{n1},{\sum }_{n=1}^N{x}_{n2},...,{\sum }_{n=1}^N{x}_{nD})$
标量SS是各数据点的平方和即${\sum }_{n=1}^N{\overrightarrow{x}}_n^2={\sum }_{n=1}^N{\overrightarrow{x}}_n^T{\overrightarrow{x}}_n={\sum }_{n=1}^N{\sum }_{i=1}^D{x}_{ni}^2$

举个例子
假设簇一有三个数据点(2, 5)、(3, 2)和(4, 3)，根据定义，簇一的聚类特征是
$$CF1=(3,(2+3+4，5+2+3),(2^2+5^2)+(3^2+2^2)+(4^2+3^2))=(3,(9，10)，67)$$

CF具有可加性：CF1=（n1,LS1,SS1），CF2=（n2,LS2,SS2），则CF1+CF2=（n1+n2, LS1+LS2, SS1+SS2）表示将两个不相交的簇合并成一个大簇的聚类特征。

举个例子
设簇C2的CF2=（3，（35,36），857），那么，由簇C1和簇C2合并而来的簇C3的聚类特征CF3计算如下：
CF3=(3+3, (9+35, 10+36), (67+857))=(6, (44, 46), 924)

聚类特征本质上是给定簇的统计汇总，可以有效地对数据进行压缩，而且基于聚类特征可以很容易地推导出簇的许多统计量和距离度量。
假设给定簇中有N个D维数据点，可用以下公式定义簇的质心$X_0$，半径R和直径D
簇质心：$${\overrightarrow{x}}_0=\frac{{\sum }_{i=1}^N{\overrightarrow{X}}_i}{N}=\frac{LS}{N}$$
簇半径：$$R=\sqrt{\frac{{\sum }_{i=1}^N({\overrightarrow{X}}_i-{\overrightarrow{X}}_0{)}^2}{N}}=\sqrt{\frac{NSS-L{S}^2}{N^2}}$$
簇直径：$$D=\sqrt{\frac{{\sum }_{i=1}^N{\sum }_{j=1}^N({\overrightarrow{X}}_i-{\overrightarrow{X}}_j{)}^2}{N(N-1)}}=\sqrt{\frac{2NSS-2L{S}^2}{N(N-1)}}$$
其中R是成员对象到质心的平均距离，D是簇中两两数据点的平均距离，这两个统计量都反映了簇内紧实度。
不同簇间的距离度量通常用曼哈顿距离，公式如下：
$$D_0=\sqrt{\frac{{\sum }_{i=1}^{N_1}{\sum }_{j=N_1+1}^{N_1+N_2}({\overrightarrow{X}}_i-{\overrightarrow{X}}_j{)}^2}{N_1{N}_2}}=\sqrt{\frac{S{S}_1}{N_1}+\frac{S{S}_2}{N_2}-\frac{2L{S}_{1}L{S}_2}{N_1{N}_2}}$$

3 聚类特征树（CF-tree）

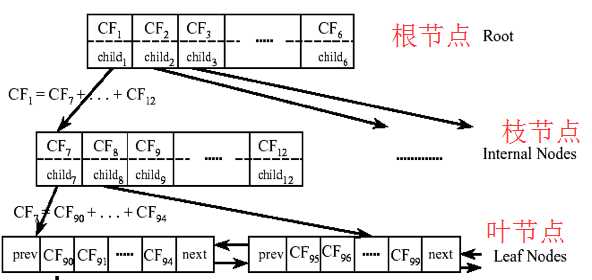
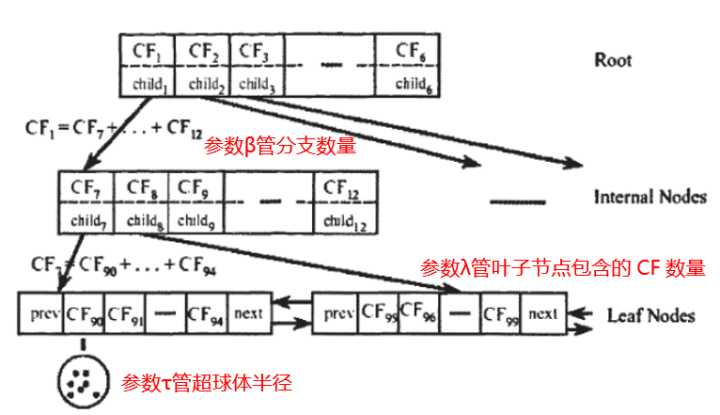
CF树存储了层次聚类的簇的特征，有三个参数：枝平衡因子$\beta$、叶平衡因子$\lambda$和空间阈值$\tau$。CF树由根节点、枝节点和叶节点构成，非叶节点中包含不多于$\beta$个形如$[C{F}_i,chil{d}_i]$的条目（entry）。其中$C{F}_i$表示该节点上子簇的聚类特征信息，指针$chil{d}_i$指向该节点的子节点。叶节点中包含不多于$\lambda$个形如$[C{F}_i]$的条目，此外每个叶节点中都包含指针prev指向前一个叶节点和指针next指向后一个叶节点。空间阈值$\tau$用于限制叶节点的子簇的大小，即所有叶节点的各条目对应子簇的直径D（或半径R）不得大于$\tau$，行如下图

枝平衡因子β，表示枝节点最大的孩子数，所有内部节点的分支不得多于 β 个,
叶平衡因子λ，表示叶子节点允许包含的最大CF数；
空间阈值 τ，表示 叶节点每个CF的最大样本半径或直径，所有类簇的半径不得大于 τ

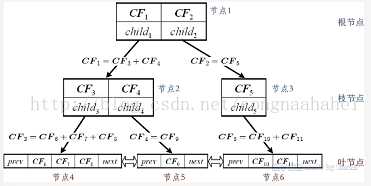
例：β=2，λ=3


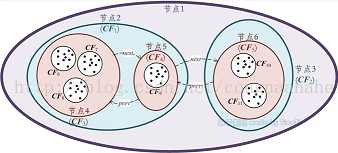
各节点及其元项代表的簇间的关系如左图所示，需要说明的是，CF树上不保存任何数据点，仅有树的结构信息以及相关的聚类特征信息，因此CF树可以达到压缩数据的效果。

4 聚类特征树的生成

最开始的 CF 树 是空的，没有任何样本，我们一边添加数据，一边进行学习。

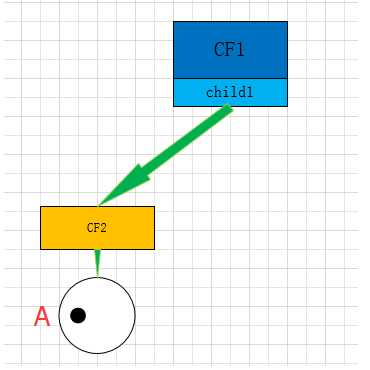
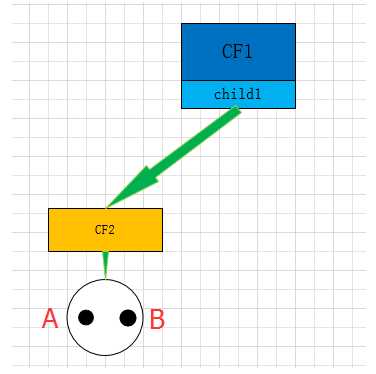
首先，读入第一条数据 A，构造一个叶子节点和一个子簇。

当引入第二个样本B时，需要判断，样本A和样本B是否在半径为 τ 的超球体范围内？

如果在，也就是说他们属于同一个CF，根据 CF 可加性，更新CF

如果不在，我们需要一个新的CF三元组，来容纳这个新的值

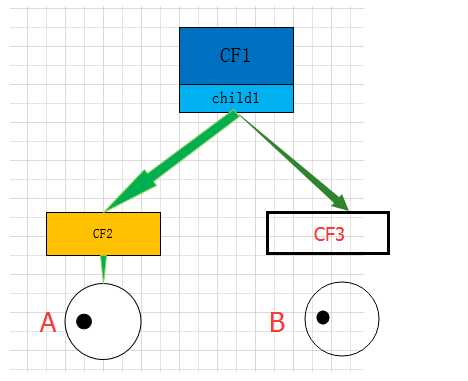
假设我们设置枝平衡因子β=2，即内部节点的分支不得多于2个。

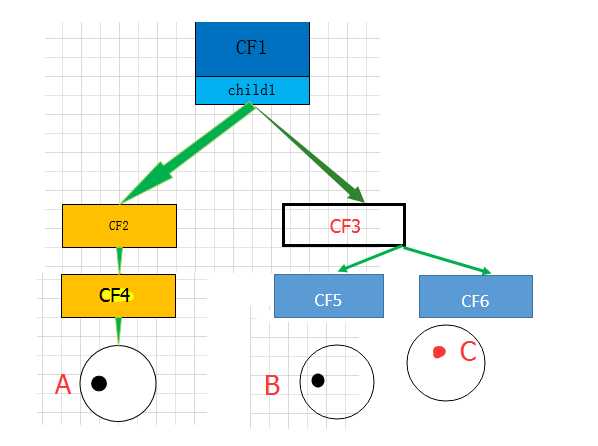
这时候来了一个点C，离CF3最近，但不属于A，B两个超球体范围内，本应该将它单独设一个分支，但是CF1的分枝数已经达到最大值，此时，我们只能选择继续向下分裂

5 总结

形象得理解了 CF 树建立的过程，我们尝试总结一下步骤：

1、初始化枝平衡因子β，叶平衡因子λ和空间阈值τ；

2、在数据库中逐个选取数据点，将数据点插入到CF树上：

（i） 从根节点开始，自上而下选择最近的孩子节点

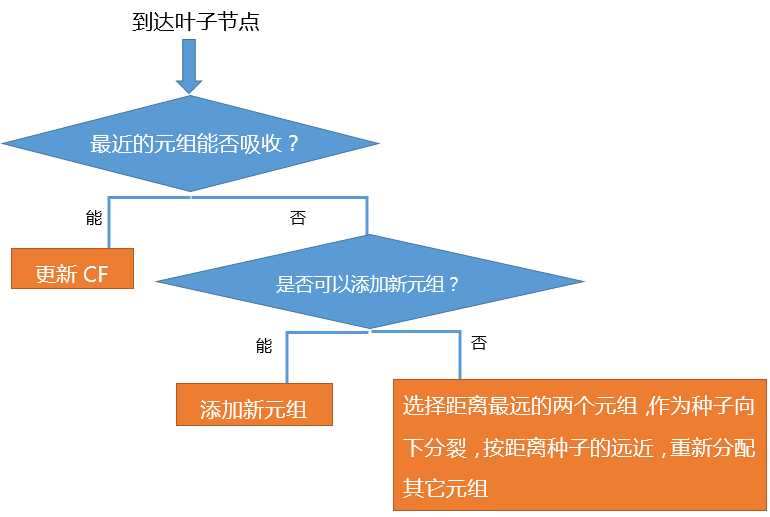
（ii） 到达叶子节点后，

3、更新每个非叶节点的CF信息，如果分裂节点，在父节点中插入新的元组，检查分裂，直到根节点

了解了CF树构建的过程，我们自然就可以理解为什么Birch算法适合于处理大数据。

（1）CF 结构概括了簇的基本信息，并且是高度压缩的，它存储了小于实际数据点的聚类信息。每个新添加的数据其作为个体消失了，将信息融入的集合簇中
（2）增量式的学习方法，不用一次将数据全部加载到内存，可以一边添加数据一边进行学习

参考文献1
参考文献2

今天的文章层次聚类(Hierarchical Clustering)——BIRCH算法详解及举例分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。