1. 流形学习概述

流形学习manifold learning，于2000年在Science杂志上首次提出，是一大类基于流形的框架，是机器学习、模式识别中的一种方法，在维数约简（降维）方面具有广泛的应用。它的主要思想是将高维的数据映射到低维，使低维的数据能够反映原高维数据的某些本质结构特征。不同于一般意义上的数据降维方法，典型如autoencoders 等通过学习得到一种参数化的模型，能够适用于任何输入向量，通常意义上的流形学习方法属于非参数方法。流形学习的前提是有一种假设，即某些高维数据，实际是一种低维的流形结构嵌入在高维空间中。流形学习的目的是将其映射回低维空间中，揭示其本质。作为一种数据降维的方式，流形学习还能够刻画数据的本质。数学意义上的流形笼统来说属于微分几何的一个分支，比较代表性的流形学习方法有等量隐射ISOMAP 、局部线性嵌入LLE、拉普拉斯特征图Laplacian Eigenmaps 、SNE与t-SNE。

2.流形的定义

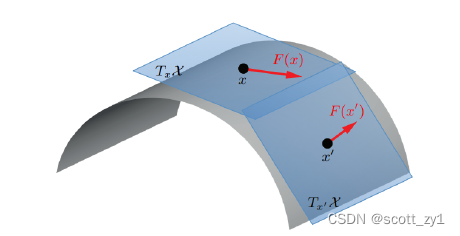
数学概念上的流形（manifold）一词源于国内拓扑学奠基人江泽涵院士翻译于德语mannigfaltigkeit（德国数学家黎曼首次提出）。笼统地讲，流形是局部欧几里德的拓扑空间。最简单的一个例子就是地球表面，它是嵌入在三维空间中的二维曲面。从地球上每个局部点看，地球似乎都是平的。更正式地说，d维流形  是定义的一个特殊空间，空间中的每个点 都有一个邻域在拓扑上等价于一个d维欧式空间，称为切空间（tangent space），表示为 。如下图所示。

黎曼流形是一个在切空间中每个点都关联内积运算的可微流形，这假设了数据点位置具有光滑性。內积运算导出距离、角度和体积的概念。內积运算的这些集合被称为黎曼度量（內积、距离、角度和体积）。可以证明，任何足够光滑的黎曼流形可以嵌入到更高维的欧几里德空间中。

汇总常用的流形学习方法，并与参数化方法Autoencoder对比如下。

3. classical MDS

最简单的流行学习算法就是multidimensional scaling(MDS)，其本质是寻找一组低维向量集，使得数据点之间的两两相似性能够尽可能接近或表达高维数据的两两相似性。具体而言，假定一个矩阵的纬度为，每一行可以表示为,定义一个Gram矩阵表示相似性如下：

以矩阵的形式定义,其中,     称为中心矩阵，现在可以定义数据嵌入后的应变量：

其中  称为中心嵌入向量，直观而言，上述表达式衡量了高维数据空间  与 低维数据嵌入在相似性上的匹配程度。最小化上述loss function 就称为classical MDS。

基于数据降维的理论可知，对于一个矩阵的最佳线性近似可采用rank 为 的截断SVD表示如下

                        ​​​​​​​        ​​​​​​​                        

其中  为半正定矩阵，令 ， 可得到最优嵌入满足：

因此得到的嵌入向量表示为                 

接下来可基于欧式距离的平方而不是原始特征，将classical MDS应用于数据集，具体而言

首先计算二次欧式距离矩阵   ,展开形式如下：

 观察可知， 与 仅仅只是在行和列相差一个比例系数 -2，由此可令

上式展开，即

根据上述分析，令    是中心kernel 矩阵降维后rank 为  的截断SVD矩阵，则 ，基于原始数据得到中心化处理矩阵 ，对应的PCA嵌入, 由此基于 可推导如下

        ​​​​​​​                       

由此得到   , 则, 即classical MDS 等价于PCA。

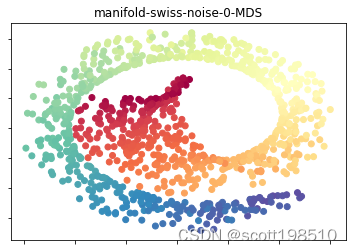
4. Kernel PCA

classical MDS是找到数据的最佳线性投影，以保持所有点之间的两两相似性。在本节中，我们考虑非线性投影。具体而言，在线性投影或嵌入中，通过定义内积矩阵来衡量相似性，在kernel PCA中采用kernel function ​​​​​​​ 来替代内积 。

                ​​​​​​​        ​​​​​​​        

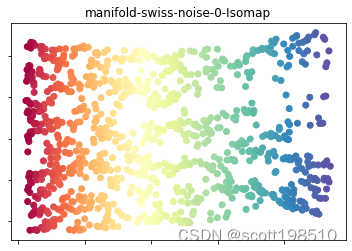
5.ISOMAP

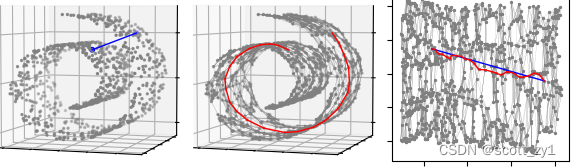
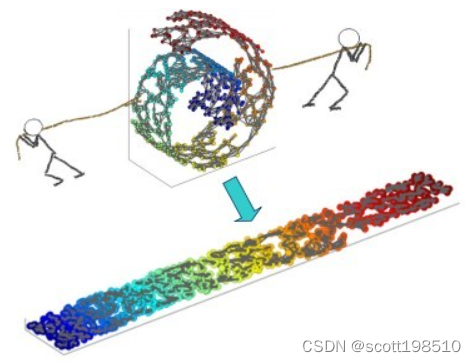
        对于非线性的流形数据，如果使用线性降维方法得到的效果不尽人意，比如下图中瑞士卷。在 ISOMAP 中，首先引入一个测地线的概念，在距离度量定义时，测地线可以定义为空间中两点的局域最短路径。形象的理解，在一个球面上，两点之间的测地线就是过这两个点的大圆的弧线。

           那么，对于非线性流形，ISOMAP 则是通过构建邻接图，利用图上的最短距离来近似测地线。在构造邻接图时，我们使用最近邻算法，对于一个点连接距离其最近的 k 个点，两点之间的距离我们则一般使用传统的欧式距离。则任意两点之间的测地线距离可以利用构建的邻接图上的最短路径进行估计，图上的最短路径问题我们可以通过 Dijkstra 或 Floyd-Warshall 算法计算。得到样本的距离矩阵后，ISOMAP 算法则使用 MDS 方法计算得到低维空间的坐标映射。

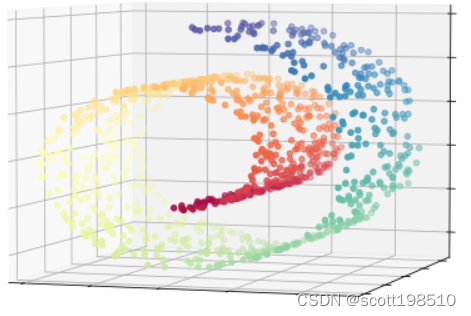
       上图中给出了利用 ISOMAP 对瑞士卷降至2D的一个格式化过程。第一幅图中标注了2个蓝色的点，其中蓝色的直线为这2个点在三维空间中的欧式距离。第二幅图中，同样是相同的两个点，我们首先利用最近邻算法 (k=10) 将瑞士卷所有的点连接为一个邻接图，其中红色的路径为这 2个点在邻接图上的最短路。第三幅图是通过 ISOMAP 算法降维至 2D的结果，其中蓝色的直线是这两个点在2D空间中的欧式距离，红色路径是 3D最短路在2D结果中的连线，可以看出两者很相近。

6. LLE方法　　　

6.1 LLE的直观理解

　   在上述ISOMAP 方法中，采用等距映射算法有一个问题就是，需要找所有样本全局的最优解，当数据量很大，样本维度很高时，计算非常耗时，鉴于这个问题，LLE通过放弃所有样本全局最优的降维，只是通过保证局部最优来降维。同时假设样本集在局部是满足线性关系的，进一步减少的降维的计算量。

6. 2 LLE思想

　　LLE首先假设数据在较小的局部是线性的，也就是说，某一个数据可以由它邻域中的几个样本来线性表示。比如我们有一个样本,我们在它的原始高维邻域里用K-近邻思想找到和它最近的三个样本 然后我们假设可以由线性表示，即：   

　　其中，为权重系数。在通过LLE降维后，我们希望在低维空间对应的投影和对应的投影也尽量保持同样的线性关系，即:                       

　　也就是说，投影前后线性关系的权重系数是尽量不变或者最小改变的。

　　从上面可以看出，线性关系只在样本的附近起作用，离样本远的样本对局部的线性关系没有影响，因此降维的复杂度降低了很多。

6.3 LLE算法流程

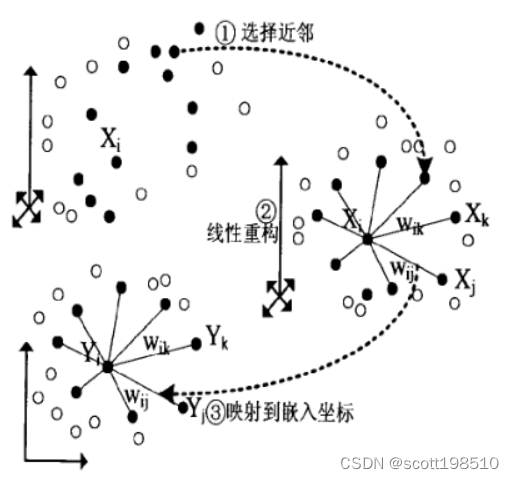
　　　　整个LLE算法的实现过程用一张图可以表示如下：

        ​​​​​​​        

　　从图中可以看出，LLE算法主要分为三步，第一步是求K近邻的过程，这个过程使用了和KNN算法一样的求最近邻的方法。第二步，就是对每个样本求它在邻域里的K个近邻的线性关系，得到线性关系权重系数W，具体过程在第三节第一部分。第三步就是利用权重系数来在低维里重构样本数据，具体算法及实现可详见本专栏博客 LLE原理及推导过程。

6.4 LLE的一些改进算法

　　LLE算法很简单高效，但是却有一些问题，比如如果近邻数k大于输入数据的维度时，我们的权重系数矩阵不是满秩的。为了解决这样类似的问题，有一些LLE的变种产生出来。比如：Modified Locally Linear Embedding(MLLE)和Hessian Based LLE(HLLE)。对于HLLE，它不是考虑保持局部的线性关系，而是保持局部的Hessian矩阵的二次型的关系。而对于MLLE，它对搜索到的最近邻的权重进行了度量，我们一般都是找距离最近的k个最近邻就可以了，而MLLE在找距离最近的k个最近邻的同时要考虑近邻的分布权重，它希望找到的近邻的分布权重尽量在样本的各个方向，而不是集中在一侧。

　　另一个比较好的LLE变种是Local tangent space alignment(LTSA)，它希望保持数据集局部的几何关系，在降维后希望局部的几何关系得以保持，同时利用了局部几何到整体性质过渡的技巧。

　　这些算法原理都是基于LLE，基本都是在LLE这三步过程中寻求优化的方法。

6.5 LLE总结

　　　LLE是广泛使用的图形图像降维方法，它实现简单，但是对数据的流形分布特征有严格的要求。比如不能是闭合流形，不能是稀疏的数据集，不能是分布不均匀的数据集等等，这限制了它的应用。下面总结下LLE算法的优缺点。

　     LLE算法的主要优点有：

　　　  1）可以学习任意维的局部线性的低维流形

　　　  2）算法归结为稀疏矩阵特征分解，计算复杂度相对较小，实现容易。

　   LLE算法的主要缺点有：

　　   1）算法所学习的流形只能是不闭合的，且样本集是稠密均匀的。 

　　   2）算法对最近邻样本数的选择敏感，不同的最近邻数对最后的降维结果有很大影响。

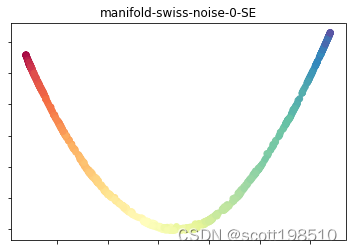
7. Laplacian Eigenmaps

Laplacian Eigenmaps 即拉普拉斯特征图，采用由图定义的距离近似于流形上的距离，基于原始的数据结点连接关系构造一个连接矩阵，数据点连接在一起的就有相似性，否则相似性为0。最终构造出Graph Laplacian matrix（图拉普拉斯矩阵）。

        ​​​​​​​        ​​​​​​​        ​​​​​​​        

 具体而言，通过优化如下loss function来找到最佳嵌入

                ​​​​​​​        

其中相似性度量采用高斯函数

        ​​​​​​​        ​​​​​​​        ​​​​​​​        ​​​​​​​        

        ​​​​​​​        

同时，为了避免得到退化的解 ， 添加约束条件 , 是对角矩阵，用于存储每个节点的自由度 .具体实现可详见本专栏博客Laplacian Eigenmaps原理及推导过程。

8. SNE与 t-SNE方法

SNE是通过仿射(affinitie)变换将数据点映射到概率分布上，主要包括两个步骤：

• SNE构建一个高维对象之间的概率分布，使得相似的对象有更高的概率被选择，而不相似的对象有较低的概率被选择。
• SNE在低维空间里在构建这些点的概率分布，使得这两个概率分布之间尽可能的相似。

 t-SNE是SNE的推广， 为了实现前面提到的保留数据的局部特征，同样应该如下要求：原先距离近的数据，降维之后距离应该也很近；原先距离远的数据，降维之后距离应该也很远。

前几种流形学习都是通过计算某种相似性或者距离，将高维的数据点向低维投影实现降维，t-SNE 中主要是将“距离的远近关系”转化为一个概率分布，每一个概率分布就对应着一个“样本间距离远近”的关系。而降维前后的数据都各自对应着一个概率分布，我们就希望这两个概率分布足够的接近。具体实现可详见本专栏博客 t-SNE原理与推导。

9.总结

        PCA、LDA等线性降维方法处理流形数据时会出现某种程度的“拥挤”或“踩踏”，上述针对流形处理都采取了某种转换，将高维数据中的距离关系进行转换，从而等效到低维空间中的数据结构并保持原有的数据本质结构。目前使用最多的还是LLE和t-SNE。

10.参考文献

1..J.B. Tenenbaum, V. de Silva, and J. C. Langford. A global geometric framework for nonlinear dimensionality reduction. Science, vol. 290, pp. 2319–2323, 2000.

2. S. T. Roweis and L. K. Saul. Nonlinear dimensionality reduction by locally linear embedding. Science, vol. 290, pp. 2323–2326, 2000.

3..M. Belkin, P. Niyogi, Laplacian Eigenmaps for Dimensionality Reduction and Data Representation. Neural Computation, Vol. 15, Issue 6, pp. 1373 –1396, 2003 .

4.Geoffrey Hinton and Sam Roweis. Stochastic Neighbor Embedding

5.Laurens van der Maaten, Geoffrey Hinton. Visualizing Data using t-SNE

6. Probabilistic Machine Learning

今天的文章机器学习中的流形学习算法 Manifold Learning分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。