My blog

思路：

n个顶点，所以要做n次矩阵乘法 (因为求回路,如果是求通路的话，就是n-1次。)，（所有的矩阵都放在一个二维数组里了~）

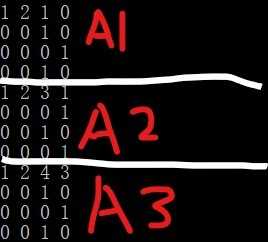
所有的矩阵都放在同一个mapp数组了，如图：看图可以解释清楚，

复杂度有点大哦~~~~~~~ 但是 不想写那些头疼的算法了……

最后求可达矩阵，只需要遍历A1的所有点，然后根据A1里点的坐标比如（i，j） 对应A2 A3（i+k*n，j）k:[0,n] 的坐标 看里面的数据是不是>0 如果是则p[i][[j]=1

最后遍历p ，如果全都是1 则判断为可达矩阵，否则不是。

代码：

/*利用邻接矩阵判断有向图是否为强连通图*/
/*思路，求可达矩阵*/
#include <iostream>
#include <cstring>
#include <string>
#include <cmath>
#include <algorithm>
#include <cstdio>
#include <queue>
#include <stack>
#define Max 1001
#define ll long long
#define inf 0x3f3f3f3f
using namespace std;
int mapp[Max][Max],p[Max][Max];
int n,m;
int main() {
	memset(mapp,0,sizeof(mapp));//大矩阵
	memset(p,0,sizeof(p));//可达矩阵 
	//顶点是从1开始标号的。
	cout<<"输入顶点的个数和弧的个数:"<<endl;
	cin>>n>>m;
	cout<<"输入各个弧的起点和终点："<<endl;
	while(m--) {
		int u,v;
		cin>>u>>v;
		mapp[u][v]++;
	}
	//邻接矩阵构造成功，检验
//	for(int i=1;i<=n;i++)
//	{
//		for(int j=1;j<=n;j++)
//		cout<<mapp[i][j]<<" ";
//		cout<<endl;
//	}
	//矩阵相乘
	//n个顶点，所以要做n次矩阵乘法 ，（所有的矩阵都放在一个二维数组里了~） 
	/*
	1 1 2
	1 2 3
	1 3 4
	1 4 5
	...
	1 n-2 n-1
	*/
	//正确 
	for(int l=1;l<=n;l++)
	{
		for(int i=1; i<=n; i++) {
		for(int j=1; j<=n; j++) {
			//每一行与每一列相乘的答案 
			for(int k=1; k<=n; k++) {
				mapp[i+l*n][j]+=mapp[i][k]*mapp[k+(l-1)*n][j];
				}
			}
		}
	 } 
	
//	//检验 正确 
//	for(int i=1;i<=n*n;i++)
//	{
//		for(int j=1;j<=n;j++)
//		{
//			cout<<mapp[i][j]<<" ";
//		}cout<<endl;
//	}
	//可达矩阵 
	for(int i=1;i<=n;i++)
	{
		p[i][i]=1; 
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			for(int k=0;k<=n;k++)
			{
//				cout<<"!!~~"<<mapp[i+k*n][j]<<endl;
				if(mapp[i+k*n][j])
				{
//					cout<<"!!! "<<i+k*n<<" "<<j<<endl;
						p[i][j]=1;
					}
			 } 
		}
	 } 
	 int flag=0;
	 //可达矩阵 
	 cout<<"可达矩阵："<<endl; 
	 for(int i=1;i<=n;i++)
	 {
	 	for(int j=1;j<=n;j++)
	 	{
		 	cout<<p[i][j]<<" ";
		 	if(p[i][j]==0)flag=1;
		 	else continue;
		 }
		 cout<<endl;

	 }
	 if(flag) cout<<"No"<<endl; 
	 else cout<<"Yes"<<endl; //是强连通图 
	return 0;
}
/*
4 7
1 1
1 2 
1 2
1 3
2 3
3 4
4 3
*/

今天的文章离散数学实践作业——判断有向图是不是强连通图分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。