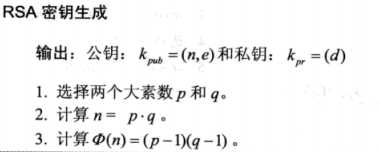非对称加密/公钥密码学（基础）

非对称加密/公钥密码学

非对称密码学和公钥密码学表示相同的东西；绝大多数非对称加密算法都基于数论函数。

先简单介绍一下对称加密算法的特点以及缺点（为什么需要非对称加密算法）：

特点：
加密和解密使用相同的秘钥；
加密函数和解密函数相同或非常类似。

缺点：
密钥的分配传输不安全；
每对用户都需要一个密钥对时，密钥个数太多；
对于用户的欺骗没有防御机制。

非对称加密：

用户A使用用户B的公钥加密明文，用户B得到密文后，使用自己的私钥解密。

上述过程中，用户B无法使用自己的公钥解密密文，只能用自己的私钥解密，其原理是 单向函数。

单向函数：

非对称加密的安全机制：

1.密钥建立：在不安全信道上建立密钥的协议有若干种，包括Diffie-Hellman密钥交换协议（DHKE）协议或RSA密钥传输协议。
2.不可否认性：可以通过数字签名算法（比如RSA、DSA或ECDSA）实现不可否认性和消息完整性。
3.身份标识：在类似银行智能卡或手机等的应用中，可使用质询-响应协议与数字签名相结合的方法识别实体。
4.加密：可使用类似RSA或Elgamal的算法对消息进行加密。

非对称加密算法的三种类型：

1.整数分解：基于因式分解大整数非常困难，代表算法RSA；
2.离散对数：最典型的包括Diffie-Hellman密钥交换、Elgamal加密或数字签名算法(DSA);
3.椭圆曲线(EC)：离散对数算法的一个推广就是椭圆曲线公钥方案；最典型的包括椭圆曲线Diffie-Hellman密钥交换(ECDH)和椭圆曲线数字签名算法(ECDSA)。

学习公钥算法前需要了解的知识：
1.欧几里得算法

假设 r(0) > r(1)

2.欧拉函数

3.费马小定理

4.欧拉定理

RSA加密算法


RSA密钥的生成（正确性不做介绍）：

RSA加密算法实例：


实际中，RSA模数n应至少为1024位，使p和q至少为512位。

小贴士：在实际运用中，可能会对RSA算法做填充。

离散对数 和 椭圆曲线 的了解可前往https://blog.csdn.net/qmickecs/article/details/76585303

数字签名：私钥签名，公钥解签名。

哈希函数：哈希函数不属于加密。

数据加密解密过程（详）：

1.用户A使用哈希函数生成明文X的摘要M，然后使用自己的私钥加密摘要M，生成数字签名N；

2.用户A使用对称加密算法加密明文X，得到密文Y（对称加密算法的密钥为K）;

3.用户A使用用户B的公钥加密对称加密算法的密钥K，得到EK；

4.用户A将数字签名N、密文Y、EK同时传给用户B;

5.用户B用自己的私钥解密EK，得到对称加密算法的密钥K；

6.用户B使用对称加密算法的密钥K解密密文Y，得到明文X;

7.用户B使用用户A的公钥解密数字签名N，得到摘要M；

8.用户B使用哈希函数哈希明文X，得到摘要M2;

9.用户B将摘要M与摘要M2做比对，如果相同，就说明明文在传输过程中没有发生改变；同时第7步也可证明，是用户A传过来的数据。

（之所以使用对称加密算法加密明文，不直接使用公钥加密明文，是因为对称加密算法的效率高）

实际中，CA证书的使用替代了上述部分步骤：

图片转自：https://blog.csdn.net/lk2684753/article/details/100160856

今天的文章非对称加密/公钥密码学（基础）分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。