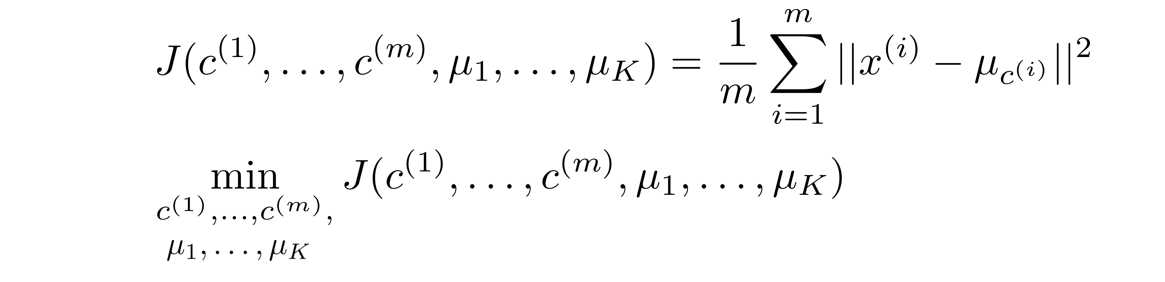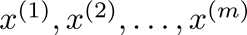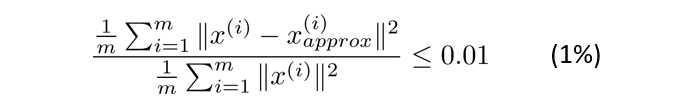【机器学习】聚类分析与主成分分析(附例题源码)

往期文章
【机器学习】回归分析
 【机器学习】Logistic回归
 【机器学习】神经网络
 【机器学习】支持向量机

文章目录

K-means算法

直观理解

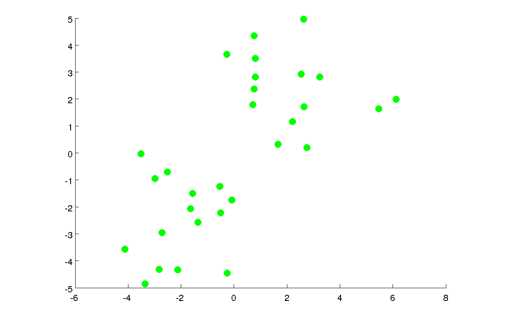
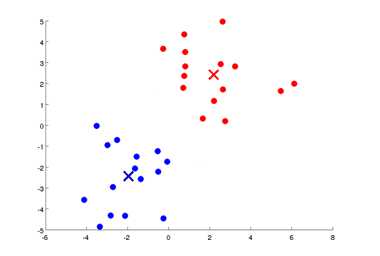
假入我有一个如上图所示无标签的数据集，现在我想将其分为两个簇，K-Means算法具体操作如下：

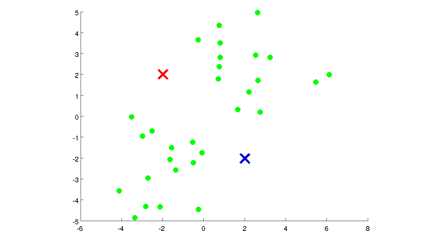
随机生成两点，这两点叫做聚类中心。

进入迭代，进行簇分配和移动聚类中心。

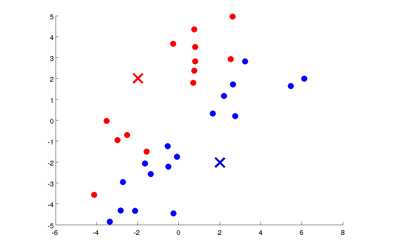
首先进行簇分配：

遍历每个绿点，看这个绿点是与红色聚类中心更近，还是与蓝色聚类中心更近，来将每个数据点分配给两个聚类中心之一。

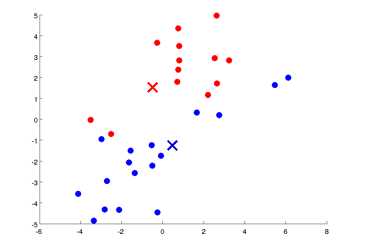
然后移动聚类中心：

将红色和蓝色的聚类中心分别移动到各自簇的均值点处，例如我将所有红色点加起来算出均值点所在的位置就是红色聚类中心应该移到的地方。

重复步骤2，当聚类中心不再改变时，也就是K均值聚合时，就可完成分类。

算法思路：

输入，包括输入K和一系列无标签的数据集，注意 $x^{(i)}$ 是n维向量，K是表示聚类出簇的个数，后面会说明如何选择K。

随机初始化，然后进入迭代。 $μ$ 表示聚类中心，例如上边的红色和蓝色的聚类中心可分别表示为 $μ_1$ 和 $μ_2$ 。

变量 $c^{(i)}$ 表示第1到K个最接近 $x^{(i)}$ 的聚类中心，也就是进行簇分配，所以 $c^{(i)}$ 是一个在1~K之间的数。

优化目标

在得出优化目标之前，我们先来了解几个变量：

$c^{(i)}$ ：被分配到的簇的聚类中心的索引值，例如第 $i$ 个样本与第五个聚类中心最近，则 $c^{(i)}=5$ 。

$μ_k$ ：第k个聚类中心。

$μ_{C^{(i)}}$ ：样本 $x^{(i)}$ 当前所属的簇，例如属于第五个簇，则 $μ_5$ 。

在理解这三个变量后，我们可得出优化目标为：

对于这个目标函数，我们要找出合适的 $c^{(1)},…,c^{(m)}$ 使得函数最小化。

随机初始化

这里的随机初始化是指算法开始时，随机设定的聚类中心，下面我们来说一下随机初始化的步骤：

聚类中心的数量小于样本数，即K<m。
随机生成聚类中心 $μ_i,…,μ_k$ 。

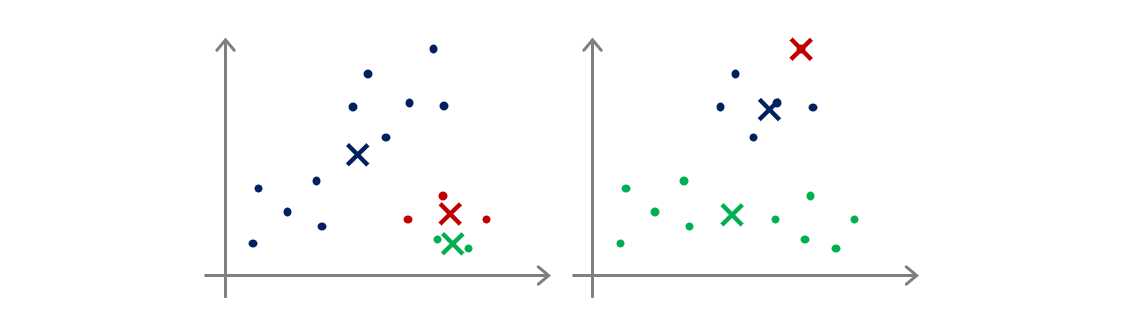
但随机生成的聚类中心可能会使结果陷入局部最优，如下图所示：

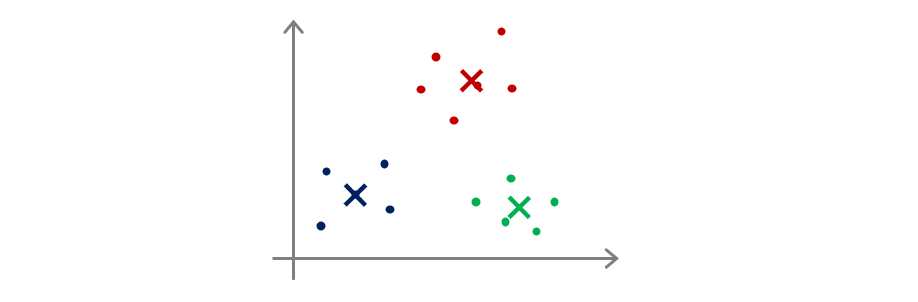
如果我们要确保结果是全局最优，如下图所示，则需要多次进行初始化，并多次运行K-Means算法

以下是相关算法，重复执行初始化和K-Means算法100次，最终取代价函数最小的那个值即可：

聚类中心个数(K)的选择

目前来说，还没有自动选择K的算法，我们只能通过可视化的图，算法的输出等等来确定K。

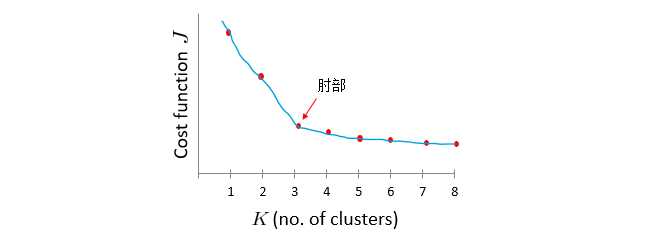
下面我们来介绍一种在选择K值时常常用到的方法，叫**“肘部法则”**。

首先我们改变K值，例如当K=1时，也就意味着所有的数据都会分到一类，然后计算出代价函数 $J$ ，继续令K=2，K=3，…，会得到类似下图所示的曲线，我们找出曲线趋于平缓的转折点，也就是**“肘部”**，这个肘部对应的K值就是聚类中心的个数。

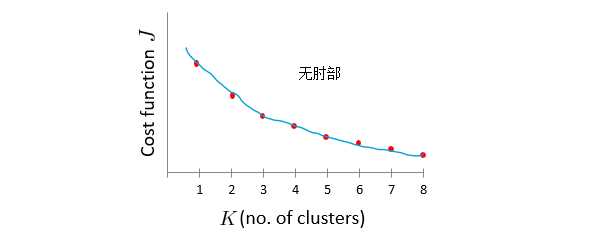
但有时候，我们得到的曲线可能不会出现肘部，也就是没有清晰的拐点，选择K=6,7,8好像都可以，优点模棱两可。

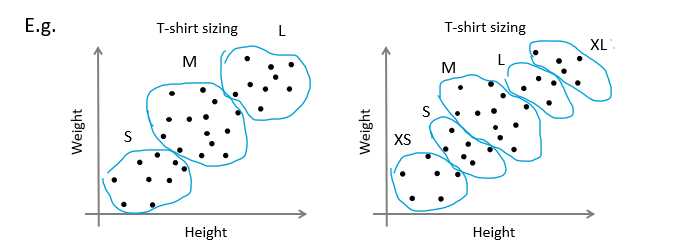
下面我们来介绍另外一种方法，就是根据我们的分类目的来进行选择，例如现在我们来对销售T恤的码数来进行分类，首先在得到大量顾客的身高和体重后，如果我最终的目的是划分为大，中，小三个码，那么我可以令K=3，如果我分为XS，S，M，L，XL则五个码，则令K=5。

降维

现在我们来介绍无监督学习的第二种算法叫做降维。

理解降维

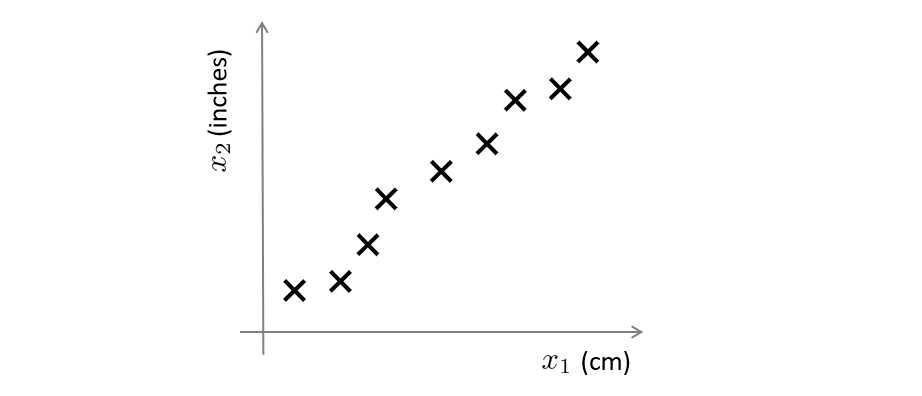
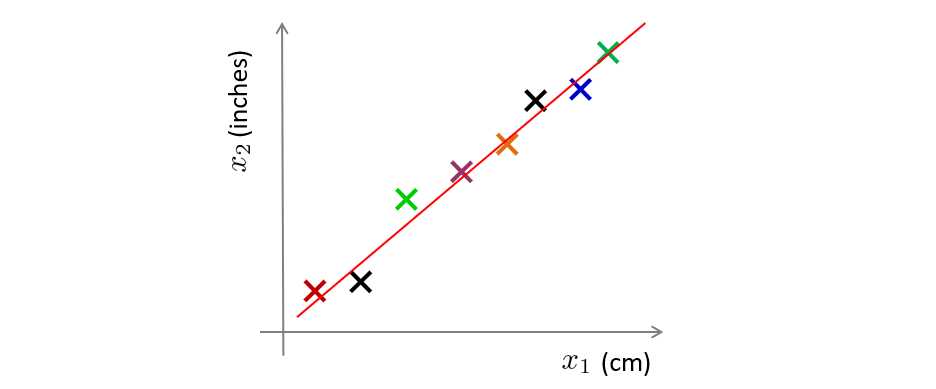
现在我们有一些样本，每个样本含有多个特征，其中 $x_1$ 表示用厘米作为单位表示物体长度， $x_2$ 表示用英寸作为单位表示物体长度。

但这样会造成长度冗余，且占用内存，我们试着将 $x_1$ 和 $x_2$ 用一种方法同时表示，也就是将数据从二维降到一维，那么如何进行降维呢？

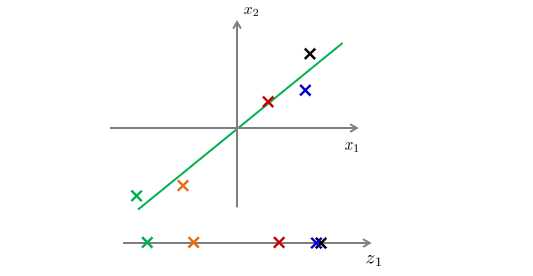
首先我们将数据点标上不同的颜色（为了更直观去理解），然后画出一条直线。

然后特征数据点投影到线上，建立新的特征 $z_1$ ：

$x^{(1)}→z^{(1)}$

$x^{(2)}→z^{(2)}$

$. . .$

$x^{(m)}→z^{(m)}$

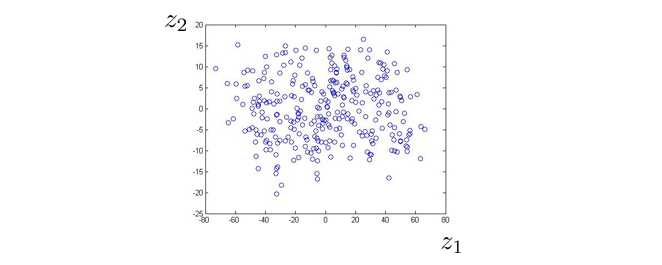
现在我只需要一个数就能确定数据点的位置了，从而减少了占用的内存：

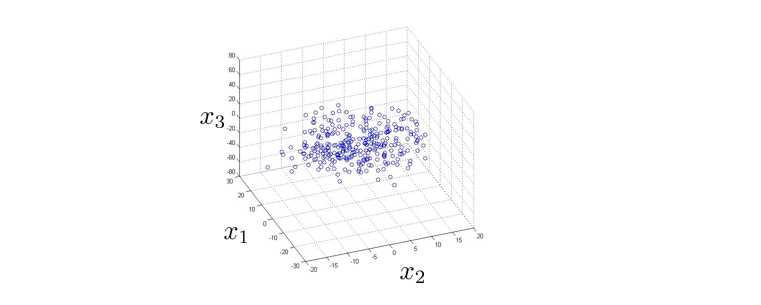
下面再来看看如何将数据从三维降到二维：

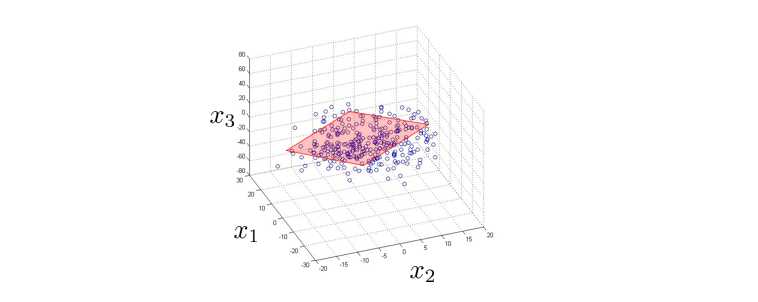
首先我们画一个平面，使数据点均匀分布在平面两侧：

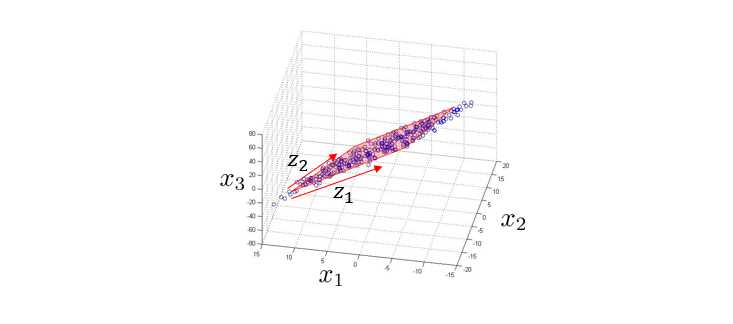
然后将数据点投影到平面上：

这时候我们就可以两个新特征 $z_1$ 和 $z_2$ 来表示数据点的位置了。

主成分分析（PCA）

直观理解

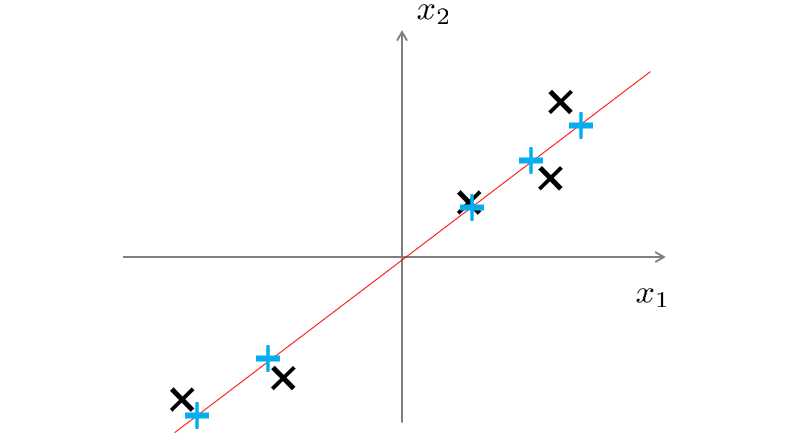
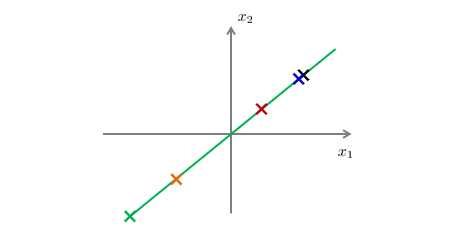
现在有一个二维的数据集，现在我想降为一维，而PCA要做的是找到一个平面（这里是直线），使得数据点与投影点之间的距离平方和（投影误差）最小，如下图：

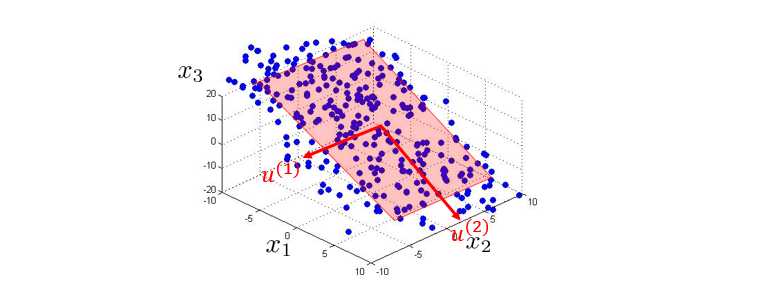
对于三维降二维问题，PCA则找出由向量 $u^{(1)}$ 和 $u^{(2)}$ 展开的平面，此平面同样使得投影误差最小。

同理，对于 $n$ 维空间降成 $k$ 维，我们要做的是将这些数据点投影到这 $k$ 个向量展开的线性子空间上。

算法步骤

给定一个训练集：

进行均值标准化

首先算出样本的均值：

$μ_j=\frac{1}{m}\sum^m_{i=1}x^{(i)}_j$

然后用 $x_j-μ_j$ 取代每个特征 $x^{(i)}_j$ .

计算出协方差矩阵以及求协方差

这里我直接调用python的包进行求解，如果想了解原理，可以看看文末参考资料链接。

压缩重现

上面我们已经讲到了将数据进行压缩的方法，那么如何将压缩后的数据 $z^{(i)}$ 还原回高维 $x^{(i)}$ 呢。

现在我们有一组数据已经完成降维：

其中 $z=U_{reduce}^Tx$ ，矩阵 $U_{reduce}$ 也是调包解决，原理可以看文末参考资料链接。

$U_{reduce}$ （n×k）协方差矩阵的特征向量单位化后按列排列出的矩阵，是正交矩阵，转置与逆相同。

现在我们对数据进行还原，因为是有损压缩，还原后的x，只是与原来的x比较接近，并不完全相等，利用上式可得 $x≈U_{reduce} z$ .

主成分数量选择

首先我们知道，PCA的作用就是最小化投影误差: $\frac{1}{m}\sum^m_{i=1}{||x^{(i)}-x^{(i)}_{approx}||}^2$

下面再来定义一下数据的总变化量（样本与原点总距离）： $\frac{1}{m}\sum^m_{i=1}{||x^{(i)}||}^2$

我们想选择k的值，也就是主成分个数，通常是使得下面不等式成立的最小k值：

算法：

先尝试 $k = 1$ ,若不满足不等式，则尝试 $k = 2$ ，依次类推，直到找到满足不等式的 $k$ .

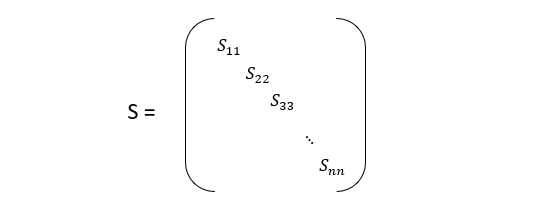
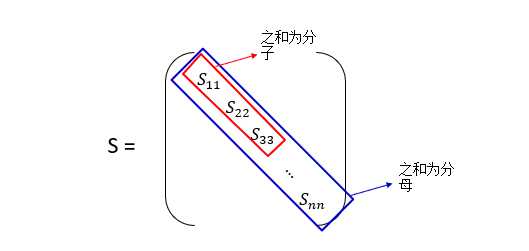
注意，当我们调包进行奇异值分解的时候还会返回一个对角矩阵S（下面有代码，可以先看看调用部分）

如果我们给定一个 $k$ ，上面的不等式可以简化成，这样做的好处是我们只需要调用一次奇异值分解即可，因为S是不变的。

$1-\frac{\sum_{i=1}^kS_{ii}}{\sum^n_{i=1}S_{ii}}≤0.01$

例如 $k = 3$ 时，分子是前三了数相加，而分母是整体相加。

我们逐渐增加 $k$ ，直到找到时不等式满足的 $k$ .

注意事项

PCA可以通过降维来提高算法的速度，但不适合用来防止过拟合问题，防止过拟合还是需要正规化来解决。

建议首先考虑用原始数据，而不是一上来就使用PCA去降维，如果达不到目的才使用PCA。

吴恩达机器学习练习7（题目和数据在下面获取）

K-Means

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.io as sio

数据可视化

data = sio.loadmat('E:\happy\ML&DL\My_exercise\ex7-k-means & PCA\data\\ex7data1.mat')
data.keys()

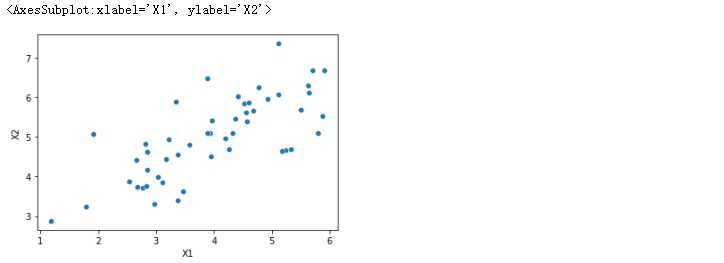
data1 = pd.DataFrame(data.get('X'), columns=['X1', 'X2'])
data1.head()

sns.scatterplot(data=data1,x='X1' ,y='X2')

data = sio.loadmat('E:\happy\ML&DL\My_exercise\ex7-k-means & PCA\data\\ex7data2.mat')
data.keys()

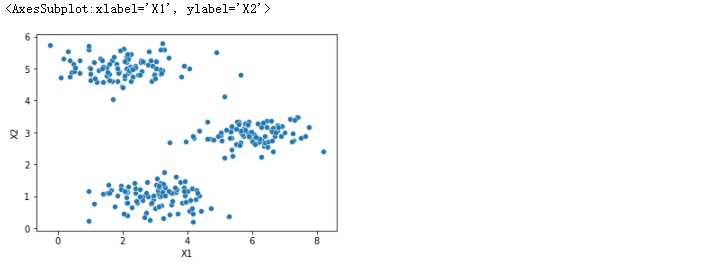
data2 = pd.DataFrame(data.get('X'), columns=['X1', 'X2'])
data2.head()

sns.scatterplot(data=data2,x='X1' ,y='X2')

聚类中心初始化

def random_init_centroids(X, k):
    X = X.values
    r = X.shape[0] #行数
    c = X.shape[1] #列数
    centroids = np.zeros((k, c))
    index = np.random.randint(0, r, k) #样本中随机抽取k个数作为聚类中心
    
    for i in range(k):
        centroids[i,:] = X[index[i],:]
    
    return centroids

random_init_centroids(data2, 3)

簇分配

def find_cluster(X, centroids):
    X = X.values
    n = X.shape[0]
    k = centroids.shape[0]
    index = np.zeros(n) #用于记录每个样本所属的聚类中心
    
    for i in range(n):
        min = 10e8
        for j in range(k):
            m = np.sum((X[i,:] - centroids[j,:]) ** 2)
            if m < min:
                min = m
                index[i] = j
                
    return index

centroids = random_init_centroids(data2, 3)
index = find_cluster(data2, centroids)

移动聚类中心

def move_centroids(X, k, index):
    X = X.values
    r = X.shape[0] #行数
    c = X.shape[1] #列数
    centroids = np.zeros((k, c))
    
    for i in range(k):
        cluster = np.where(index == i) #属于一个簇的样本
        centroids[i,:] = (np.sum(X[cluster,:], axis=1) / len(cluster[0]))
        
    return centroids

move_centroids(data2, 3, index)

运行K-Means

def run_k_means(X, centroids, k, max_iter=10):
    for i in range(max_iter):
        index = find_cluster(X, centroids)
        centroids = move_centroids(X, k, index)

    return index, centroids

centroids = random_init_centroids(data2, 3)
index, centroids = run_k_means(data2, centroids, 3)

index

centroids

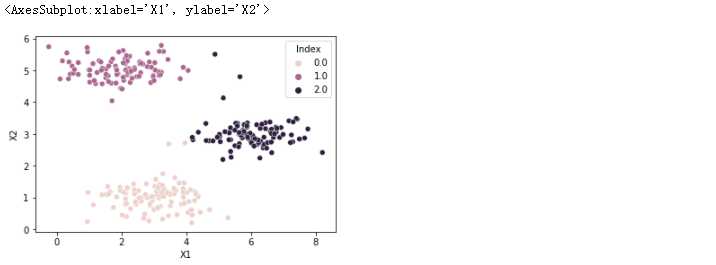
data2['Index'] = index 
data2

sns.scatterplot(data=data2, x='X1', y='X2', hue='Index')

K-Means图像压缩

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

def random_init_centroids(X, k):
    r = X.shape[0] #行数
    c = X.shape[1] #列数
    centroids = np.zeros((k, c))
    index = np.random.randint(0, r, k) #样本中随机抽取k个数作为聚类中心
    
    for i in range(k):
        centroids[i,:] = X[index[i],:]
    
    return centroids

def find_cluster(X, centroids):
    n = X.shape[0]
    k = centroids.shape[0]
    index = np.zeros(n) #用于记录每个样本所属的聚类中心
    
    for i in range(n):
        min = 10e8
        for j in range(k):
            m = np.sum((X[i,:] - centroids[j,:]) ** 2)
            if m < min:
                min = m
                index[i] = j
                
    return index

def move_centroids(X, k, index):
    r = X.shape[0] #行数
    c = X.shape[1] #列数
    centroids = np.zeros((k, c))
    
    for i in range(k):
        cluster = np.where(index == i) #属于一个簇的样本
        centroids[i,:] = (np.sum(X[cluster,:], axis=1) / len(cluster[0]))
        
    return centroids

def run_k_means(X, centroids, k, max_iter=10):
    for i in range(max_iter):
        index = find_cluster(X, centroids)
        centroids = move_centroids(X, k, index)

    return index, centroids

将图片下载为ndarray形式，这里也可以直接导入数据中的bird_small.mat

from skimage import io

pic = io.imread('E:\happy\ML&DL\My_exercise\ex7-k-means & PCA\data\\bird_small.png')
io.imshow(pic)

pic.shape

数据预处理，先进行归一化和降维

np.max(pic)

#归一化
pic = pic / 255
#降维
pic = np.reshape(pic, (pic.shape[0] * pic.shape[1], pic.shape[2]))
pic.shape

由题目可知图像中由16中颜色，那我们可选择k=16

#运行K-Means
centroids = random_init_centroids(pic, 16)
index, centroids = run_k_means(pic, centroids, 16)

centroids.shape, index.shape

#将每个像素点与聚类中心进行匹配
pic_zip = centroids[index.astype(int),:]
pic_zip.shape

final_pic = pic_zip.reshape(128,128,3)

#可以发现，压缩后的图片特征并没有改变
io.imshow(final_pic)

利用sklearn实现

from sklearn.cluster import KMeans

model = KMeans(n_clusters=16, n_init=100, n_jobs=-1)

model.fit(pic)

index = model.predict(pic)
index.shape

centroids = model.cluster_centers_
centroids.shape

final_pic = centroids[index, :].reshape(128,128,3)

io.imshow(final_pic)

主成分分析

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.io as sio

data = sio.loadmat('E:\happy\ML&DL\My_exercise\ex7-k-means & PCA\data\\ex7data1.mat')
data

X = data.get('X')
X.shape

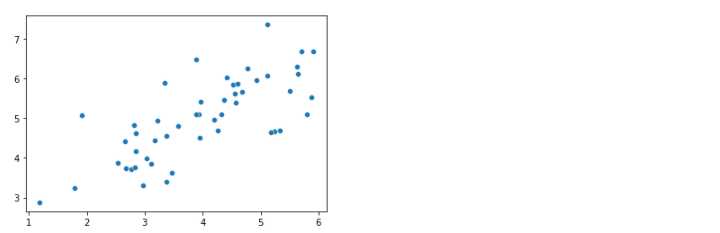
sns.scatterplot(data=X, x=X[:,0], y=X[:,1])

降维

先进行数据归一化，计算出协方差矩阵，再调用svd进行奇异值分解

def pca(X):
    #归一化
    X = (X - X.mean()) / X.std()
    
    #协方差矩阵
    X = np.matrix(X)
    cov = (X.T * X) / X.shape[0]
    
    #奇异值分解
    U, S, V = np.linalg.svd(cov)
    
    return U, S, V

U, S, V = pca(X)
U.shape, S.shape, V.shape

得到主成分U后，进行降维，k是维数，我们现在将这个二维数组降为一维

$z=U_{reduce}^Tx$

def dimension_reduction(X, U, k):
    U_reduce = U[:,:k]
    X = np.matrix(X)
    
    return X * U_reduce

z = dimension_reduction(X, U, 1)
z.shape

压缩重现

$x≈U_{reduce} z$

def reproduce_data(z, U, k):
    U_reduce = U[:,:k]
    return z * U_reduce.T

X_recover = reproduce_data(z, U, 1)
X_recover.shape

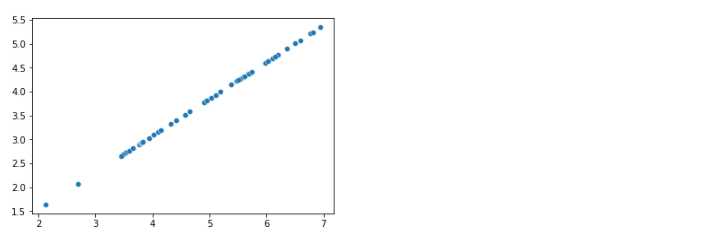
X_recover = np.array(X_recover)
sns.scatterplot(data=X_recover, x=X_recover[:,0], y=X_recover[:,1])

PCA处理面部特征

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.io as sio

mat = sio.loadmat('E:\happy\ML&DL\My_exercise\ex7-k-means & PCA\data\\ex7faces.mat')
mat

X = mat.get('X')
#调整图像的方向,每行的数据代表一个面部特征，这些在题目中有说到
X = np.array([x.reshape(32,32).T.reshape(1024) for x in X])
X.shape

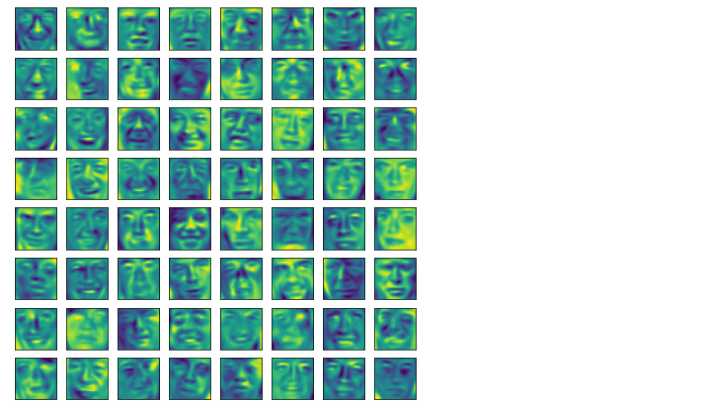
#画出n个面部
def plot_image(X):
    size = int(np.sqrt(X.shape[1]))

    # 随机选64个训练样本
    sample_images = X[:64, :]
    
    fig, ax_array = plt.subplots(nrows=8, ncols=8,
                                    sharey=True, sharex=True, figsize=(8, 8))

    for r in range(8):
        for c in range(8):
            ax_array[r, c].imshow(sample_images[8 * r + c].reshape((size, size)))
            plt.xticks(np.array([]))
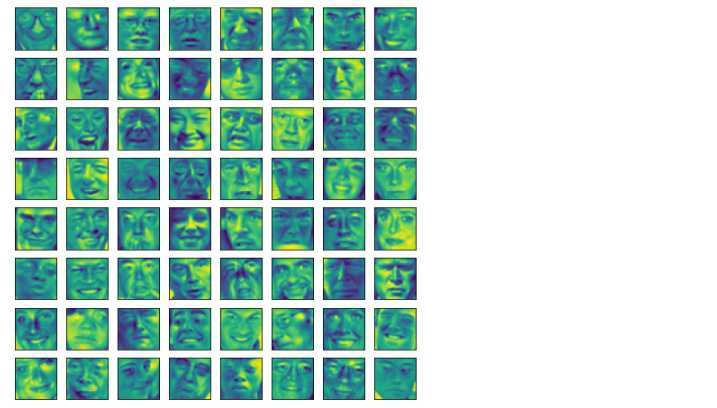
            plt.yticks(np.array([]))

plot_image(X)

#归一化
def normalize(X):
    #注意这里是每一列进行归一化，每列对应一种特征
    n = X.shape[1]
    
    for i in range(n):
        X[:, i] = (X[:, i] - X[:, i].mean()) / X[:, i].std()
        
    return X

def pca(X):
    X_norm = normalize(X)
    
    X_norm = np.matrix(X_norm)
    cov = (X_norm.T * X_norm) / X_norm.shape[0]
    
    U, S, V = np.linalg.svd(cov)
    
    return U, S, V

def dimension_reduction(X, U, k):
    U_reduce = U[:,:k]
    X = np.matrix(X)
    
    return X * U_reduce

def reproduce_data(Z, U, k):
    U_reduce = U[:,:k]
    return Z * U_reduce.T

#运行pca，得到主成分U
U, S, V = pca(X)
U.shape

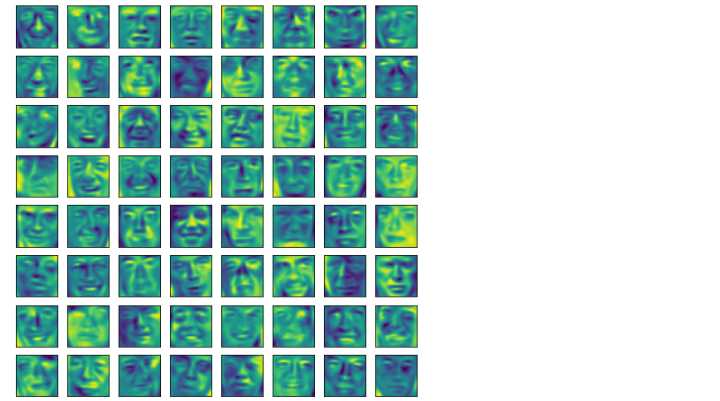
#降维(k=100)
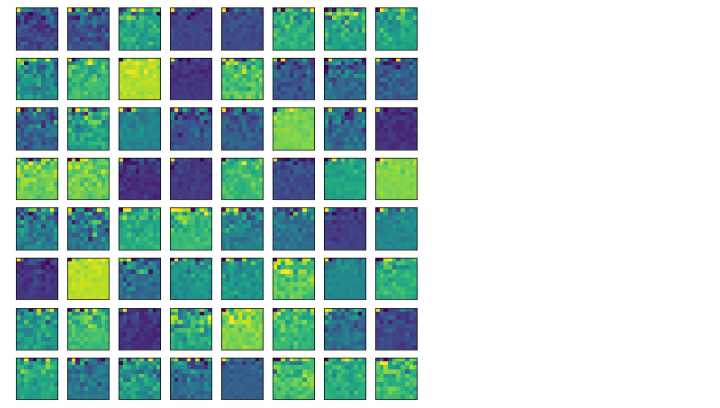
Z = dimension_reduction(X, U, 100)
plot_image(Z)

压缩重现

X_recover = reproduce_data(Z, U, 100)
plot_image(X_recover)

用sklearn进行PCA

from sklearn.decomposition import PCA

#维数k=100
model = PCA(n_components=100)
Z = model.fit_transform(X)

Z.shape

plot_image(Z)

X_recover = model.inverse_transform(Z)
X_recover.shape

plot_image(X_recover)

源码和例题获取

关注公号“大拨鼠Code”，回复“机器学习”可领取上面例题的源文件，jupyter版本的，例题和数据也一起打包了，之前的练习也在里面，感谢支持。

参考资料：

[1]https://zhuanlan.zhihu.com/p/77151308
[2]https://www.bilibili.com/video/BV164411b7dx
[3]https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes

今天的文章【机器学习】聚类分析与主成分分析(附例题源码)分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。

版权声明：本文内容由互联网用户自发贡献，该文观点仅代表作者本人。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容，请发送邮件至举报，一经查实，本站将立刻删除。
如需转载请保留出处：https://bianchenghao.cn/32088.html

【机器学习】聚类分析与主成分分析(附例题源码)

文章目录

K-means算法

直观理解

优化目标

随机初始化

聚类中心个数(K)的选择

降维

理解降维

主成分分析（PCA）

直观理解

算法步骤

压缩重现

主成分数量选择

注意事项

吴恩达机器学习练习7（题目和数据在下面获取）

K-Means

K-Means图像压缩

主成分分析

PCA处理面部特征

源码和例题获取

相关推荐

发表回复