0.前言
XGBoost不仅在单机上通过OMP实现高度并行化,还通过MPI接口与近似分位点算法(论文中是weighted quantiles sketch)实现高效的分布式并行。其中weighted quantiles sketch框架基于 ϵ -approximate quantile近似分位点算法。不得不说分位点算法在分布式系统、流式系统中使用是个很天才的想法,很多分布式算法的基石。早在2001年,M.Greenwald和S. Khanna提出了GK Summay分位点近似算法(ϵ−approximate ϕ−quantile),直到到2007年被Q. Zhang和W. Wang提出的多层level的merge与compress/prune框架进行高度优化,而被称为A fast algorithm for approximate quantiles,目前XGBoost框架套用A fast algorithm算法结构。
本文主要介绍GK Summay算法,后续博客会持续更新分布式GK Summay算法以及A fast algorithm for approximate quantiles算法,最后还会分析XGBoost中使用的weighted quantiles sketch算法,博客内容来源主要是原始论文与Emory大学的流式数据库的课程内容,本文仅提取出关键内容加入笔者的个人理解,有错误还望谅解与告知。
1.背景
ϕ−quantile 分位点概念:排序为 rank=⌊ϕN⌋ 的元素,其中 N 为序列中元素的个数。考虑以下例子数据:
11 , 21 , 24 , 61 , 81 , 39 , 89 , 56 , 12 , 51
查询
ϕ−quantile
分位点所在数据前,需要对无序数据进行排序:
排序后很容得到:
0.5−quantile
对应
rank=5
,值为39。 此外还有,
0.1−quantile
对应
rank=1
,值为11。
ϵ−approximate ϕ−quantile 分位点概念:考虑误差近似,即给定误差 ϵ 和分位点 ϕ ,只需要给定排序区间 r′∈[(ϕ−ε)N, (ϕ+ε)N] 内任意元素即可。类似地,给定 ε=0.1,ϕ=0.5 ,可得rank值在区间 {
4,5,6} 。给定区间内任意元素,都满足排序误差 ϵN 要求。
为了满足对数据近似分位点的频繁查询,考虑以下几种场景:
1. 固定不变的数据集
2. 流式数据,数据长度不断增加
3. 数据源分布存储,但数据长度固定
4. 数据源分布存储+流式数据,数据长度不断增加
对于场景1,可以对数据进行预排序,每次查询采用二分法精确查找,时间复杂度为 O(logN) 。考虑排序误差 ϵN , 我们可以对数据进行分桶,分桶长度为 ϵN 来保证误差,即分 1/ϵ 个桶,时间复杂度降低为 O(log(1/ϵ)) ,简单的离线排序和分桶都属于offline算法,无法满足场景2、3、4场景,这就需要本文介绍online算法来构建查询summary。
2. GK Summary算法
2.1 GK Summary定义
GK Summary原本是针对流式系统分位点查询设计的,基于上述场景2。对于 ϵ−approximate 分位点查询,可以构建查询summary结构,包含 m 个summary tuple的集合:
{(v1,min1,max1),(v2,min2,max2),...,(vm,minm,maxm)}
定义:
vi
为命中第
i
个summary的代表值,简单起见,
vi
定义为
rank=mini
对应值,summary的
rank
区间为
[mini,maxi]
。
约束:为了满足给定误差
ϵN
,
maxi−mini≤ϵN
。证明:显而易见。
流式数据是不断更新,这种summary结构存在缺点:每次插入中间值,需要更新插入位置后面的summary,更新复杂度高。流式数据插入更新频率比查询频率要更高,必须优先解决数据插入构建summary的复杂度。
对此,Greenwald与Khanna提出对数据插入更新友好的GK Summary结构,相对于存绝对值,GK Summary采用相对值的结构,类似地,包含 m 个summary tuple的集合:
(v0,g0,Δ0),(v1,g1,Δ1),...,(vs−1,gs−1,Δs−1)
定义:
vi
为命中第
i
个summary的代表值,
rmin(v)
为
v
所在summary的下界,
rmax(v)
为
v
所在summary的上界,则
gi
、
Δi
定义如下:
rmin(vi)−rmin(vi−1)1, i>0, i=0
rmax(vi)−rmin(vi)0, i<s−1, i=s−1
为了便于理解,
gi
、
Δi
关系如下图:
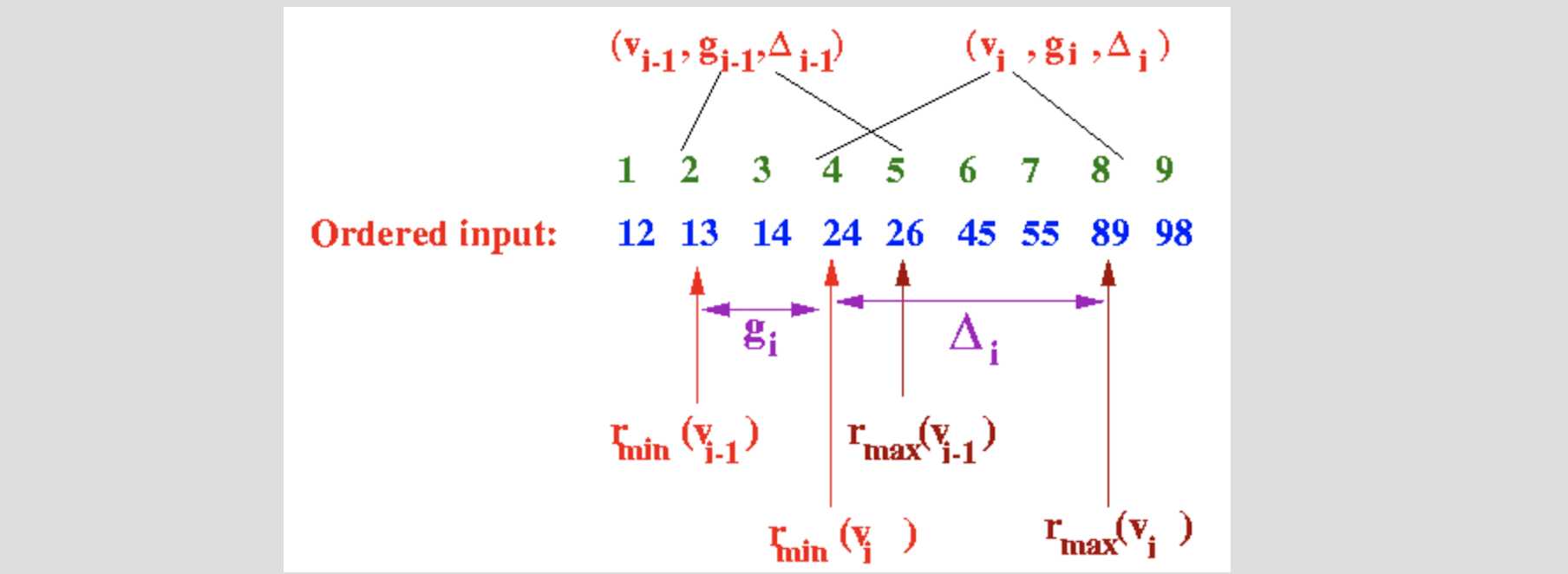
边界条件:
v0
为数据中最小值,
vs−1
为数据中最大值。等价于第一种定义的summary,排序相对值转化为绝对值,满足以下性质:
性质1: rmin(vi)=∑ij=0gi , 由 gi 定义,可以证明:
此外,边界设定
rmin(v0)=g0=1
,得证。
性质2: rmax(vi)=∑ij=0gi+Δi , 由性质1与定义 Δi=rmax(vi)−rmin(vi) 可得
性质3: ∑s−1j=0gi=N , 由性质2与边界设定 Δs−1=0 可得。
约束:为了满足给定误差 ϵN , maxi(gi+Δi)≤2ϵN 。证明如下:
设最大误差为 e=maxi(gi+Δi)/2 , 则 ∀ gi+Δi≤2e≤2ϵN
1) 首先考虑边界情况: r>N−e , 直接返回 vs−1 ,对应 rank=N ,此时误差为 N−r<e
2) 一般情况: r≤N−e , 找到最小的 j ,使得
rmax(vj)>r+e
因此,查询返回为
vj−1
, 其代表区间在
[r−e,r+e]
内,满足误差
ϵN
要求,得证。更直观的图示如下:

Summary查询过程:上述证明揭示了对于任意分位点
ϕ
,计算出排序位置
r
:1)找到最小
j
,使得
rmax(vj)>r+e
,则返回
vj−1
值,2)如果找不到则返回
vs−1
。
只要流式系统中每个时刻都维持这种summary结构,每次查询都能满足精度要求,但是流式数据实时更新,需要解决新增数据的summary更新问题。
2.2 GK Summary插入insert
流式系统数据实时更新,不断产生新数据,数据量不断增加,尽管查询近似度 ϵ 不变,随着数据量增加, ϵN 不断变大。为了保证误差,任何时刻都要保证满足约束 maxi(gi+Δi)≤2ϵN 。首先考虑数据 v 插入情况的summary更新:
1) 最小值边界情况:
v<v0
2) 最大值边界情况: v>vs−1 , 则插入summary为 (v,1,0)
3) 一般情况: vi−1≤v<vi ,则插入summary为 (v,1,gi+Δi−1)
证明:对于情况1)与2),显而易见的。对于情况3):
summary内部tuple按照对应的 v 排序,新增summary是插入到第
i−1
s−1
Δ
新增summary必须满足 g≥1 , g+Δ≤gi+Δi ,如果不满足则没有必要插入,因为前后2个summary可以覆盖新增的summary,选择 g=1 的主要原因是有利于后期summary的delete,后续会谈到,设置 Δ=gi+Δi−1 能使得 g+Δ≤2ϵN ,原则上 Δ≤⌊2ϵN⌋−1 任意值即可,后续可以看到新增非边界的summary tuple的 Δ=⌊2ϵN⌋−1 。
2.3 GK Summary删除delete与compress
每次数据插入都需要新增summary,summary不能持续增加而不删除,因此到达一定程度需要对summary进行delete。为了时刻满足 maxi(gi+Δi)≤2ϵN ,GK Summary 的delete操作:
如果存在: gj+...gi+gi+1+Δi+1≤2ϵN ,
则可以用 (vi+1,gj+...+gi+gi+1,Δi+1) 来替代 {
(vj,gj,Δj)...(vi,gi,Δi),(vi+1,gi+1,Δi+1)}
换句话说:
1)删除summary集合: {
(vj,gj,Δj)...(vi,gi,Δi)}
2)更新 (vi+1,gi+1,Δi+1)⇒(vi+1,gj+...+gi+gi+1,Δi+1)
delete操作特性:只改变 vi+1 所在summary的 gi+1 , 并不改变 Δi+1 。也就是说 Δ 越小,在满足误差约束下,具有合并更多summary的潜力。
为了追求效率,根据delete性质,GK提出compress操作,首先说明论文的概念:
1. Fullness: 如果
gi+Δi=⌊2ϵN⌋
2. Capacity:由于delete操作 Δ 不变性,因此summary达到full,
g
Δ
3. Bands:compress操作主要是减少summary总数,每个summary的元素覆盖数coverage取决于 g , 因此需要保持
g
Δ
p=⌊2ϵN⌋
对于 band=α , capactity 区间为 [2α,2α+1) , Δ 对应区间
(p−2α+1,p−2α]
summaryi
band
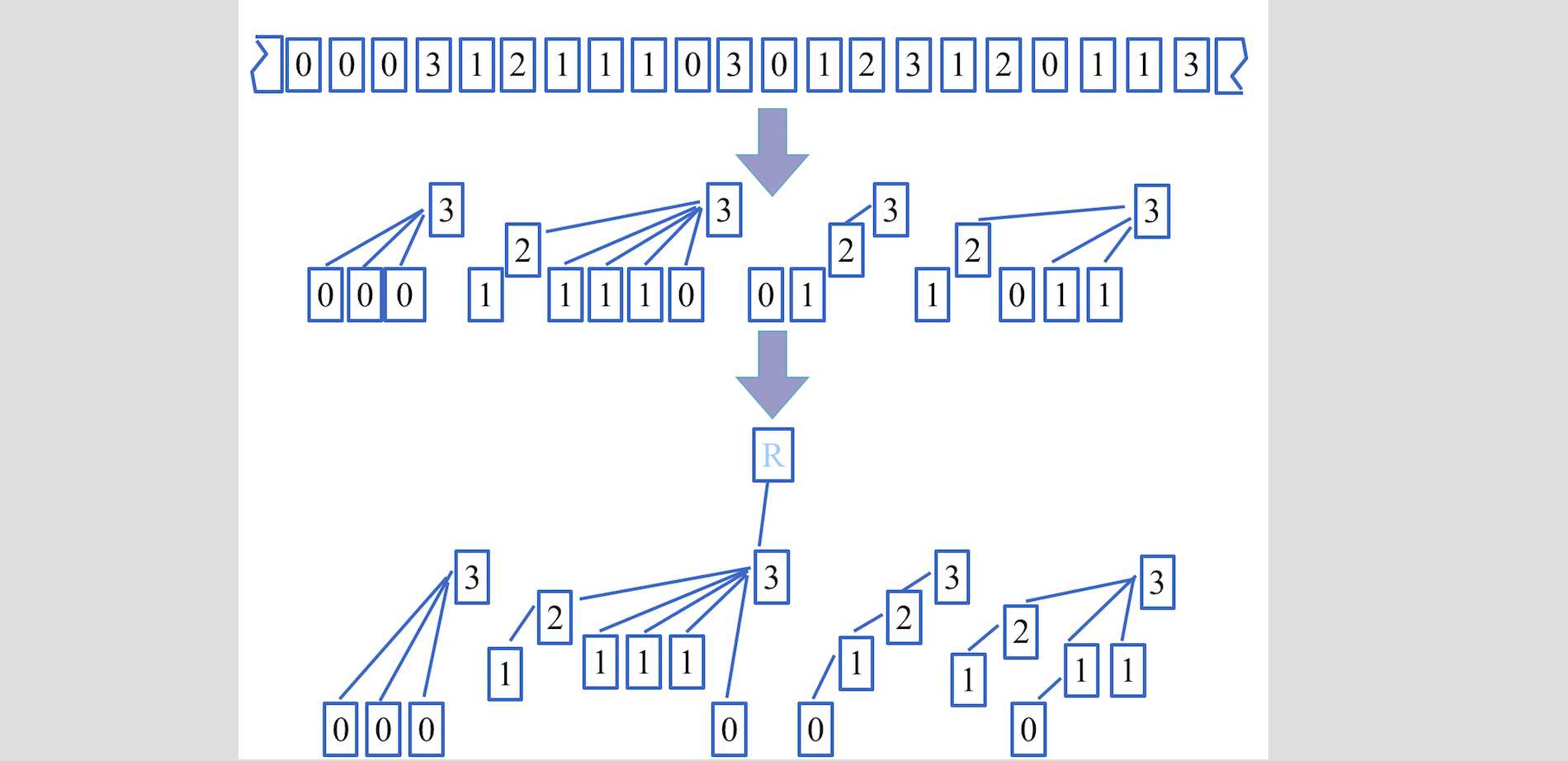
band
V
summary 更新过程中如何保证这一性质?
1)每次新数据会插入新 summary , Δ=⌊2ϵN⌋−1 , 对应 band=0 ,为最小值,除非单独节点,否则一定为右边节点的子节点。
2)合并策略:对于 summaryi , summaryi+1 合并,合并更新到 band 值较小的 summary 上。
因此,上述操作会维持这种 band 树结构性质。此外,满足上述条件,论文中给出基于 band 的compress算法:
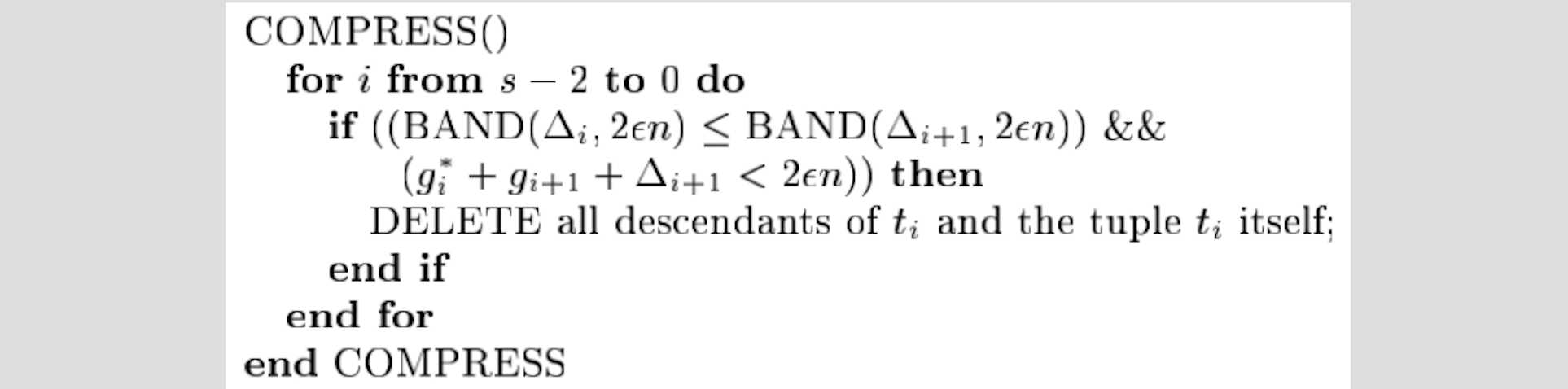
算法从右往左扫描,其中 g∗ 为当前节点与其所有子节点 g 总和,如果遇到:
BAND(Δi,2ϵn)≤BAND(Δi+1,2ϵn)
2.4 GK Summary算法
此外,需要明确compress操作执行时机:有时候原来的summary是不可合并的,但是随着数据量
N

论文还证明了以下性质和结论,由于章节内容过多,下面仅放置结论,首先继续说个概念:
Coverage:每个summary tuple会cover新增数据,对于 summaryi ,cover数据来源:1)直接cover:即单个数据插入生成的summary直接merge到 summaryi ;2)间接cover:即该数据原本被merge到 summaryj , 而 summaryj 又merge到 summaryi 。每个数据初始插入都为 (v,1,⌊2ϵN⌋−1) ,开始阶段 Δ =0,其中
g
性质1:任何时刻, band=α 的summary覆盖的数据点不可能来源于 band=β 的summary,其中 β>α
性质2:任何时刻,所有 band∈[0,α] 构成的summary集合,覆盖数据总和数上界为 2α/ϵ
性质3:任何时刻,给定 band=α ,最多 3/(2ϵ) 个父节点
性质4:任何时刻,给定 band=α ,最多 4/ϵ 个右侧兄弟节点是full的summary
性质5:任何时刻, band=α 的summary总数上界为 11/(2ϵ)
结论:任何时刻,summary的总个数上界为: 11/(2ϵ)log2(2ϵN) 。性质5直接可得该结论。
参考文献
- GK Summary算法论文:http://infolab.stanford.edu/~datar/courses/cs361a/papers/quantiles.pdf
- Emory大学Stream DB System课程关于ϵ-approximate ϕ-quantile材料:http://www.mathcs.emory.edu/~cheung/Courses/584-StreamDB/Syllabus/08-Quantile/Greenwald.html
- Emory大学Stream DB System课程关于GK Summary算法材料:
http://www.mathcs.emory.edu/~cheung/Courses/584-StreamDB/Syllabus/08-Quantile/Greenwald2.html
今天的文章GK Summay算法(ϵ−approximate ϕ−quantile)分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/32414.html
