matlab做聚类分析

转载一：

Matlab提供了两种方法进行聚类分析。

一种是利用 clusterdata函数对样本数据进行一次聚类，其缺点为可供用户选择的面较窄，不能更改距离的计算方法；

另一种是分步聚类：（1）找到数据集合中变量两两之间的相似性和非相似性，用pdist函数计算变量之间的距离；（2）用 linkage函数定义变量之间的连接；（3）用 cophenetic函数评价聚类信息；（4）用cluster函数创建聚类。

1．Matlab中相关函数介绍

1.1 pdist函数

调用格式：Y=pdist(X,’metric’)

说明：用 ‘metric’指定的方法计算 X 数据矩阵中对象之间的距离。’

X：一个m×n的矩阵，它是由m个对象组成的数据集，每个对象的大小为n。

metric’取值如下：

‘euclidean’：欧氏距离（默认）；‘seuclidean’：标准化欧氏距离；

‘mahalanobis’：马氏距离；‘cityblock’：布洛克距离；

‘minkowski’：明可夫斯基距离；‘cosine’：

‘correlation’： ‘hamming’：

‘jaccard’： ‘chebychev’：Chebychev距离。

1.2 squareform函数

调用格式：Z=squareform(Y,..)

说明： 强制将距离矩阵从上三角形式转化为方阵形式，或从方阵形式转化为上三角形式。

1.3 linkage函数

调用格式：Z=linkage(Y,’method’)

说 明：用‘method’参数指定的算法计算系统聚类树。

Y：pdist函数返回的距离向量；

method：可取值如下：

‘single’：最短距离法（默认）； ‘complete’：最长距离法；

‘average’：未加权平均距离法； ‘weighted’： 加权平均法；

‘centroid’：质心距离法； ‘median’：加权质心距离法；

‘ward’：内平方距离法（最小方差算法）

返回：Z为一个包含聚类树信息的（m-1）×3的矩阵。

1.4 dendrogram函数

调用格式：[H，T，…]=dendrogram(Z,p，…)

说明：生成只有顶部p个节点的冰柱图（谱系图）。

1.5 cophenet函数

调用格式：c=cophenetic(Z,Y)

说明：利用pdist函数生成的Y和linkage函数生成的Z计算cophenet相关系数。

1.6 cluster 函数

调用格式：T=cluster(Z,…)

说明：根据linkage函数的输出Z 创建分类。

1.7 clusterdata函数

调用格式：T=clusterdata(X,…)

说明：根据数据创建分类。

T=clusterdata(X,cutoff)与下面的一组命令等价：

Y=pdist(X,’euclid’);

Z=linkage(Y,’single’);

T=cluster(Z,cutoff);

2. Matlab程序

2.1 一次聚类法

X=[11978 12.5 93.5 31908;…;57500 67.6 238.0 15900];

T=clusterdata(X,0.9)

2.2 分步聚类

Step1 寻找变量之间的相似性

用pdist函数计算相似矩阵，有多种方法可以计算距离，进行计算之前最好先将数据用zscore函数进行标准化。

X2=zscore(X); %标准化数据

Y2=pdist(X2); %计算距离

Step2 定义变量之间的连接

Z2=linkage(Y2);

Step3 评价聚类信息

C2=cophenet(Z2,Y2); //0.94698

Step4 创建聚类，并作出谱系图

T=cluster(Z2,6);

H=dendrogram(Z2);

分类结果：{
加拿大}，{
中国，美国，澳大利亚}，{
日本，印尼}，{
巴西}，{
前苏联}

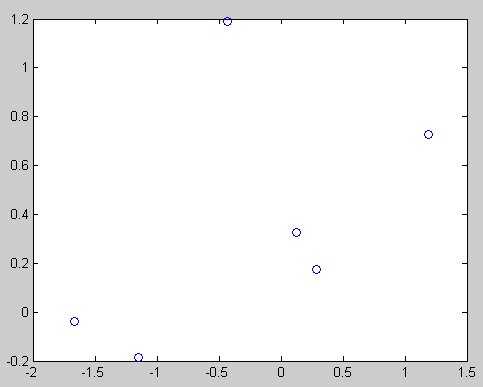
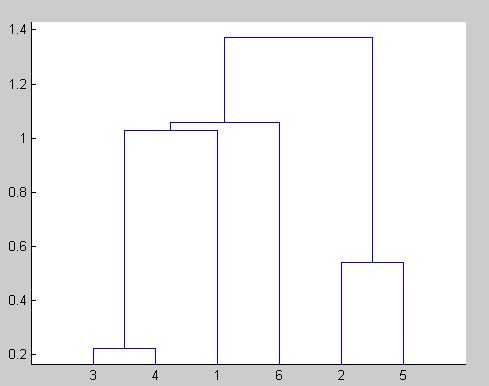
MATLAB的统计工具箱中的多元统计分析中提供了聚类分析的两种方法：
1.层次聚类 hierarchical clustering

2.k-means聚类

这里用最简单的实例说明以下层次聚类原理和应用发法。

层次聚类是基于距离的聚类方法，MATLAB中通过pdist、linkage、dendrogram、cluster等函数

来完成。层次聚类的过程可以分这么几步：

(1) 确定对象（实际上就是数据集中的每个数据点）之间的相似性，实际上就是定义一个表征对

象之间差异的距离，例如最简单的平面上点的聚类中，最经常使用的就是欧几里得距离。

这在MATLAB中可以通过Y=pdist（X）实现，例如
>> X=randn(6,2)
X =
    -0.4326     1.1892
    -1.6656    -0.0376
     0.1253     0.3273
     0.2877     0.1746
    -1.1465    -0.1867
     1.1909     0.7258
>> plot(X(:,1),X(:,2),’bo’)    %给个图，将来对照聚类结果把

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~图1~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

>> Y=pdist(X)
Y =
   Columns 1 through 14
     1.7394     1.0267     1.2442     1.5501     1.6883     1.8277     1.9648     0.5401    

2.9568     0.2228     1.3717     1.1377     1.4790     1.0581
   Column 15
     2.5092
例子中X数据集可以看作包含6个平面数据点，pdist之后的Y是一个行向量，15个元素分别代表X

的第1点与2-6点、第2点与3-6点,……这样的距离。那么对于M个点的数据集X，pdist之后的Y

将是具有M*(M-1)/2个元素的行向量。Y这样的显示虽然节省了内存空间，但对用户来说不是很易

懂，如果需要对这些距离进行特定操作的话，也不太好索引。MATLAB中可以用squareform把Y转

换成方阵形式，方阵中<i，j>位置的数值就是X中第i和第j点之间的距离，显然这个方阵应该是

个对角元素为0的对称阵。
>> squareform(Y)
ans =
          0     1.7394     1.0267     1.2442     1.5501     1.6883
     1.7394          0     1.8277     1.9648     0.5401     2.9568
     1.0267     1.8277          0     0.2228     1.3717     1.1377
     1.2442     1.9648     0.2228          0     1.4790     1.0581
     1.5501     0.5401     1.3717     1.4790          0     2.5092
     1.6883     2.9568     1.1377     1.0581     2.5092          0
这里需要注意的是，pdist可以使用多种参数，指定不同的距离算法。help pdist把。
另外，当数据规模很大时，可以想象pdist产生的Y占用内存将是很吓人的，比如X有10k个数据点

，那么X占10k*8*2Bytes=160K，这看起来不算啥，但是pdist后的Y会有10k*10k/2*8Bytes=400M

。怕了把，所以，废话说在前面，用MATLAB的层次聚类来处理大规模数据，大概是很不合适的。
(2) 确定好了对象间的差异度（距离）后，就可以用Z=linkage(Y)来产生层次聚类树了。
>> Z=linkage(Y)
Z =
     3.0000     4.0000     0.2228
     2.0000     5.0000     0.5401
     1.0000     7.0000     1.0267
     6.0000     9.0000     1.0581
     8.0000    10.0000     1.3717
对于M个元素的X，前面说了Y是1行M*(M-1)/2的行向量，Z则是(M-1)*3的矩阵。
Z数组的前两列是索引下标列，最后一列是距离列。例如上例中表示在产生聚类树的计算过程中

，第3和第4点先聚成一类，他们之间的距离是0.2228，以此类推。要注意的是，为了标记每一个

节点，需要给新产生的聚类也安排一个标识，MATLAB中会将新产生的聚类依次用M+1,M+2,….依

次来标识。比如第3和第4点聚成的类以后就用7来标识，第2和第5点聚成的类用8来标识，依次类

推。
通过linkage函数计算之后，实际上二叉树式的聚类已经完成了。Z这个数据数组不太好看，可以

用dendrogram(Z)来可视化聚类树。

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~图2~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

可以看到，产生的聚类树的每一层都是一个倒置的U型（或者说是个n型，~~），纵轴高度代表了

当前聚类中两个子节点之间的距离。横轴上标记出了各个数据点索引下标。
稍微注意以下的是，dendrogram默认最多画30个最底层节点，当然可是设置参数改变这个限制，

比如dendrogram(Z,0)就会把所有数据点索引下标都标出来，但对于成千上万的数据集合，这样

的结果必然是图形下方非常拥挤。看你的应用目的了，随你玩~

(3)初步的聚类树画完后，还要做很多后期工作的，包括这样的聚类是不是可靠，是不是代表了

实际的对象分化模式，对于具体的应用，应该怎样认识这个完全版的聚类树，产生具有较少分叉

的可供决策参考的分类结果呢？这都是需要考虑的。

MATLAB中提供了cluster, clusterdata, cophenet, inconsistent等相关函数。

cluster用于剪裁完全版的聚类树，产生具有一定cutoff的可用于参考的树。
clusterdata可以认为是pdist,linkage,cluster的综合，当然更简易一点。
cophenet和inconsistent用来计算某些系数，前者用于检验一定算法下产生的二叉聚类树和实际

情况的相符程度（就是检测二叉聚类树中各元素间的距离和pdist计算产生的实际的距离之间有

多大的相关性），inconsistent则是量化某个层次的聚类上的节点间的差异性（可用于作为

cluster的剪裁标准）。

后面这些的理解，大概需要对聚类有一个更深刻更数学的认识，我也不是很清楚，就不多说了。

from http://hi.baidu.com/coralliu/blog/item/dbde033b168fedeb15cecbe5.html

 

MATLAB提供了两种方法进行聚类分析：

1、利用clusterdata 函数对数据样本进行一次聚类，这个方法简洁方便，其特点是使用范围较窄，不能由用户根据自身需要来设定参数，更改距离计算方法；

2、分步聚类：（1）用pdist函数计算变量之间的距离，找到数据集合中两辆变量之间的相似性和非相似性；（2）用linkage函数定义变量之间的连接；（3）用cophenetic函数评价聚类信息；（4）用cluster函数进行聚类。

下边详细介绍两种方法:

1、一次聚类

Clusterdata函数可以视为pdist、linkage与cluster的综合，一般比较简单。

【clusterdata函数：

调用格式：T=clusterdata(X,cutoff)     

                     等价于Y=pdist(X,’euclid’); Z=linkage(Y,’single’); T=cluster(Z,cutoff) 】

2、分步聚类

（1）求出变量之间的相似性

用pdist函数计算出相似矩阵，有多种方法可以求距离，若此前数据还未无量纲化，则可用zscore函数对其标准化

【pdist函数：调用格式：Y=pdist(X,’metric’)

说明：X是M*N矩阵，为由M个样本组成，每个样本有N个字段的数据集

         metirc取值为：’euclidean’：欧氏距离（默认）‘seuclidean’：标准化欧氏距离;‘mahalanobis’：马氏距离… 】

pdist生成一个M*(M-1)/2个元素的行向量，分别表示M个样本两两间的距离。这样可以缩小保存空间，不过，对于读者来说却是不好操作，因此，若想简单直观的表示，可以用squareform函数将其转化为方阵，其中x(i,j)表示第i个样本与第j个样本之的距离，对角线均为0.

（2）用linkage函数来产生聚类树

【linkage函数：调用格式：Z=linkage(Y,’method’)

说明：Y为pdist函数返回的M*(M-1)/2个元素的行向量，

   method可取值：‘single’：最短距离法（默认）；’complete’：最长距离法；

                                   ‘average’：未加权平均距离法；’weighted’:加权平均法

                              ‘centroid’： 质心距离法；      ‘median’：加权质心距离法；

                               ‘ward’：内平方距离法（最小方差算法）】

返回的Z为一个(M-1)*3的矩阵，其中前两列为索引标识，表示哪两个序号的样本可以聚为同一类，第三列为这两个样本之间的距离。另外，除了M个样本以外，对于每次新产生的类，依次用M+1、M+2、…来标识。

为了表示Z矩阵，我们可以用更直观的聚类数来展示，方法为：dendrogram(Z), 产生的聚类数是一个n型树，最下边表示样本，然后一级一级往上聚类，最终成为最顶端的一类。纵轴高度代表距离列。

         另外，还可以设置聚类数最下端的样本数，默认为30，可以根据修改dendrogram(Z,n)参数n来实现，1<n<M。dendrogram(Z,0)则表n=M的情况，显示所有叶节点。

（3）用cophenetic函数评价聚类信息

【cophenet函数:   调用格式：c=cophenetic(Z,Y)

   说明：利用pdist函数生成的Y和linkage函数生成的Z计算cophenet相关系数。】

cophene检验一定算法下产生的二叉聚类树和实际情况的相符程度,就是检测二叉聚类树中各元素间的距离和pdist计算产生的实际的距离之间有多大的相关性，另外也可以用inconsistent表示量化某个层次的聚类上的节点间的差异性。

（4）最后，用cluster进行聚类，返回聚类列。