遗传算法
遗传算法的实现
遗传算法的一次迭代称为一代,每一代都有一组解。新的一组解不但可以有选择的保留一些适度值高的旧的解,而且可以包括一些由其它解结合得到的新解。最初的一组解(初始群体)是随机生成的,之后的每组解由遗传操作生成。每个解都通过一个与目标函数相关的适应度函数给予评价,通过遗传过程不断重复,达到收敛,而获得问题的最优解
-
编码:在二进制遗传算法中,自变量是以二进制字符串的形式表示的,因此需要将空间坐标转换成相应的数字串
- 如,一个三维正整数优化问题的各自变量均满足 0 ≤ x i ≤ 15 0\leq x_i \leq 15 0≤xi≤15,它的一个解为 x = [ 570 ] x=[5 7 0] x=[570],在二进制遗传算法中,这个解对应的写成 x = [ 010101110000 ] x=[0101 0111 0000] x=[010101110000],那么010101110000就是解x对应的编码
-
染色体与基因:在遗传算法中,为了与生物遗传规律对应,每一个解被称为一个个体,它对应的编码称为染色体(或者基因串)。组成染色体每一个编码元素称为基因
- 染色体010101110000有12个基因
- 当优化问题的维数和自变量的范围不同时,个体的编码长度也就不同
-
Hamming 悬崖
- 在10进制中,255+1=256;而在二进制中,如果染色体的位数是一定的,它的最大数值+1得到的是染色体放入最小数值
- 为了翻越Hamming悬崖,个体的所有位上的基因需要同时改变。由于二进制编码的遗传操作实现翻越悬崖的可能性非常小,这会使计算时出现停滞不前的现象
- 对于多维、高精度要求的连续函数优化问题,可采用10进制的实数编码遗传算法改进这一缺陷
-
初始群体一群猪出现了
- 遗传算法的初始解是随机生成的一组解,称为初始群体。在初始群体中,个体数目M越大,搜索范围就越广,效果也就越好,但是每代遗传操作时间也会越长,运行效率也较低;反之,M越小,搜索的范围越窄,每代遗传操作的时间越短,遗传算法的运算速度就可以提高,但降低了群体的多样性,有可能引起遗传算法的早熟现象(即无法获得全局最优解)
- 通常M的取值范围为20~100
- 由于初始群体中的个体是随机产生的,每个个体的基因常采用均匀分布的随机数来生成,因此初始群体中的个体素质一般不会太好,即它们的目标函数值与最优解差距较远
-
适应度函数与适度值每头猪的生存能力
- 适应度函数:为体现染色体的适应能力而引入的对每个染色体进行度量的函数
- 对一个群体中第i条染色体,通过对其目标函数值转换所得到的数值称为适度值,用 f i f_i fi表示
- 由于在遗传算法中,一次迭代后得到的是一个群体,用群体中每一个个体适度值构成的比例系数(称为存活率)作为确定个体是否应该被遗传到下一代
- 用 ∑ f i \sum f_i ∑fi表示一个群体的适度值总和,第i个染色体的适度值 f i f_i fi占总值的比例 f i / ∑ f i f_i/\sum f_i fi/∑fi被视为该染色体在下一代中可能存活的概率,即存活率
- 注:对寻找最大值的优化问题,其适应度函数可以直接选用目标函数;而对寻找最小值的最优化问题,其适应度函数可以是一个大的正数减去目标函数。总之,适度值必须为正数或零
-
遗传操作是模拟自然界生物进化过程中发生的繁殖、染色体之间的交叉和突变现象而生成新的、更优解的过程
-
遗传操作之选择大自然觉得这头猪老了,收走:按一定规则从原始群体中随机选取若干对个体作为繁殖后代的群体
- 选择根据新个体的适度值或存活率进行,个体的适度值或存活率越大,被选中的概率越大
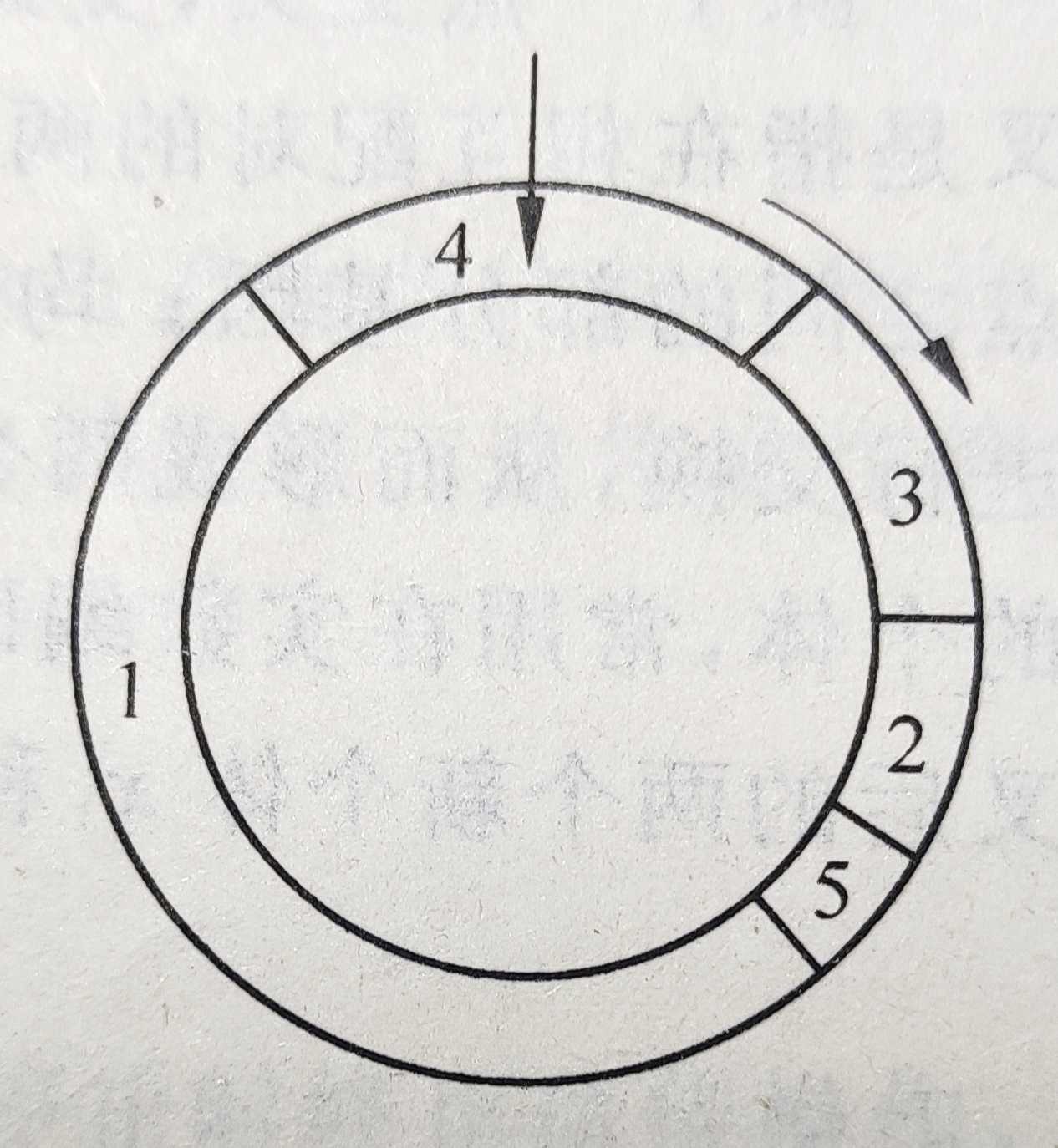
- 选择操作可以采用偏置轮盘选择(roulette wheel selection,RWS)方法
- 偏置轮盘中的区域大小与适度值成正比例,每转动一轮转盘,指针将随机地指向轮盘中的个体,这一个体就作为新一代群体中的一个个体,经过多次选择便产生初始群体
- 偏置轮盘中的区域大小与适度值成正比例,每转动一轮转盘,指针将随机地指向轮盘中的个体,这一个体就作为新一代群体中的一个个体,经过多次选择便产生初始群体
- 选择操作是从旧的群体中选出优秀者,但并不生成新的个体
-
遗传操作之交叉猪爸爸和猪妈妈有了孩子:利用来自不同染色体的基因通过交换和重组来产生新一代染色体,从而产生下一代新的个体。通过交叉操作,遗传算法的搜索能力得以大大提高
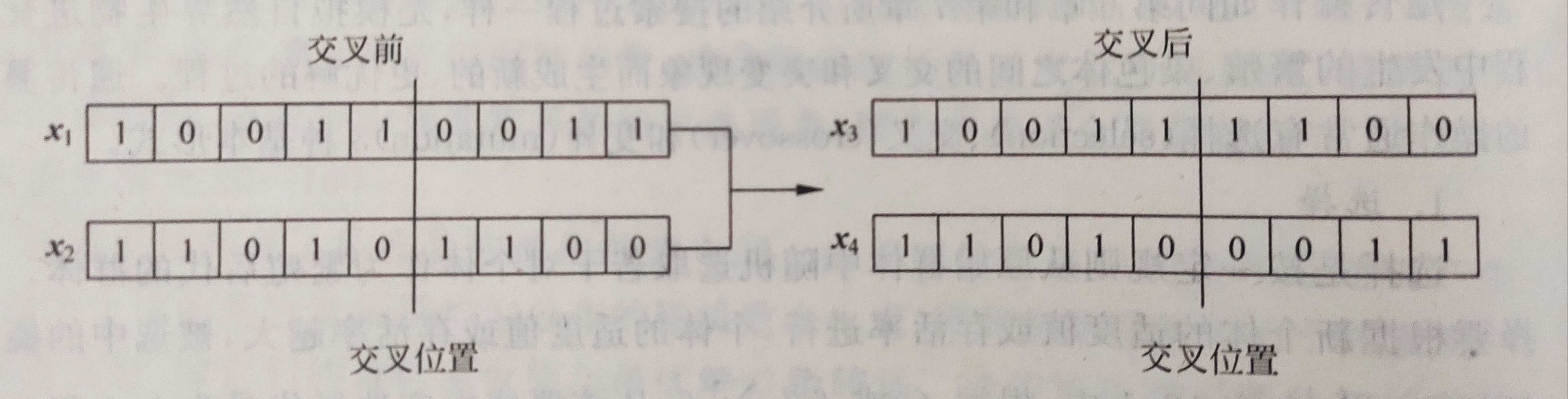
- 操作过程:在当前群体中任选取两个个体,按给定的交叉概率 P c > r a n d o m [ 0 , 1 ] P_c>random[0,1] Pc>random[0,1]在染色体的基因链上选取交叉位置,将这两个个体从该位置起的末尾部分基因互换得到两个新的染色体
- 交叉操作的方式:
- 一点交叉:在相互配对的两个个体基因编码串中随机设置一个交叉点,并交换交叉点之后的尾部基因
- 两点交叉:在相互配对的两个个体基因编码串中随机设置两个交叉点,并交换交叉点之间的部分基因
- 一致(均匀)交叉:两个相互配对的个体的每一位基因都以相同的概率进行交换,从而形成两个新的个体
- 算术交叉:由两个个体的线性组合二产生出新的个体,常用在实数编码的遗传算法中
- 设对 x 1 x_1 x1和 x 2 x_2 x2两个个体进行算术交叉,则交叉后的新个体为 x 1 ′ = α x 1 + ( 1 − α ) x 2 x_1’=\alpha x_1+(1-\alpha )x_2 x1′=αx1+(1−α)x2
x 2 ′ = ( 1 − α ) x 1 + α x 2 x_2’=(1-\alpha ) x_1+\alpha x_2 x2′=(1−α)x1+αx2
式中, α ∈ ( 0 , 1 ) \alpha \in (0,1) α∈(0,1)为一随机数
- 设对 x 1 x_1 x1和 x 2 x_2 x2两个个体进行算术交叉,则交叉后的新个体为 x 1 ′ = α x 1 + ( 1 − α ) x 2 x_1’=\alpha x_1+(1-\alpha )x_2 x1′=αx1+(1−α)x2
- 一点交叉:在相互配对的两个个体基因编码串中随机设置一个交叉点,并交换交叉点之后的尾部基因
- 交叉操作是产生新个体的主要方法之一,因此交叉概率 P c P_c Pc应取较大值。但 P c P_c Pc取过大值可能会破坏群体中的优良模式,对进化计算产生不利的影响。若 P c P_c Pc取值较小,则产生新个体的速度较慢,算法效率低
- 遗传算法交叉操作概率 P c P_c Pc的取值范围一般为0.59~0.99
-
遗传操作之变异猪宝宝变异了,有的会飞了,有的天生站不起来:变异增加了遗传算法找到接近最优解的能力,可以维持群体的多样性,防止出现早熟
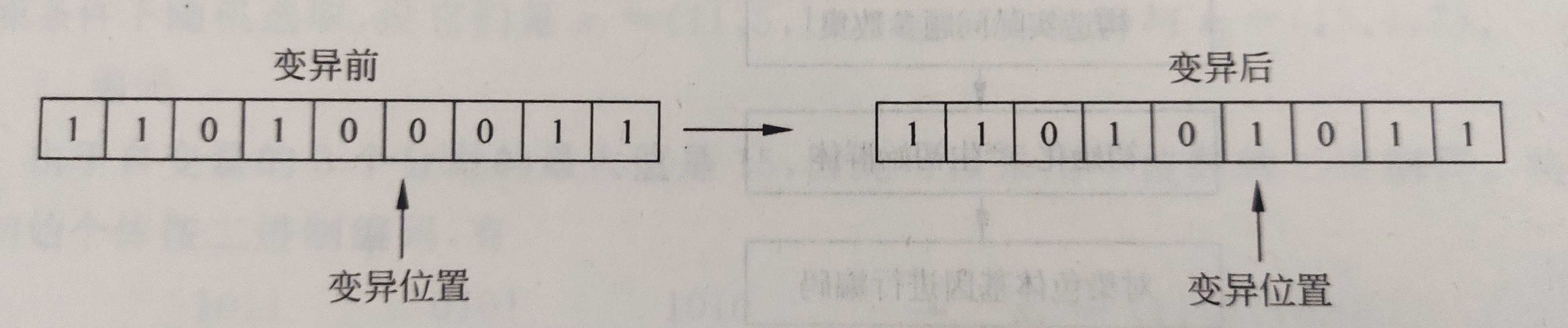
- 变异是按给定的变异概率 P m > r a n d o m [ 0 , 1 ] P_m>random[0,1] Pm>random[0,1]改变某个体的某一基因值,以生成一个新的个体
- 变异操作方式:
- 在二进制编码中,就是将变异位置处的基因由0变为1,或由0变为1
- 对于实数编码的变异操作可按下式执行 x ′ = x + 2 ( α − 0.5 ) x m a x x’=x+2(\alpha -0.5)x_{max} x′=x+2(α−0.5)xmax式中, α ∈ ( 0 , 1 ) \alpha \in (0,1) α∈(0,1)为一随机数,x为变异前个体, x m a x x_{max} xmax是x在变异操作中的最大可能改变值,x’是变异后个体
- 在二进制编码中,就是将变异位置处的基因由0变为1,或由0变为1
- 变异概率 P m P_m Pm不宜选取过大,过大可能会把群体中较好的个体变异掉,一般取0.0001~0.1,如果变异概率大于0.5,遗传算法就退化为随机搜索法
-
终止这个猪种群繁衍到终止的时候的现状
- 根据终止进化代数N,一般取值范围为100~500
- 根据适度值的最小偏差满足要求的偏差范围
- 根据适度值的变化趋势,当适度值逐渐趋于缓和或者停止时终止遗传操作,即群体中的最优个体在连续若干代没有改进或平均适度值在连续若干代基本没有改进后即可停止
-
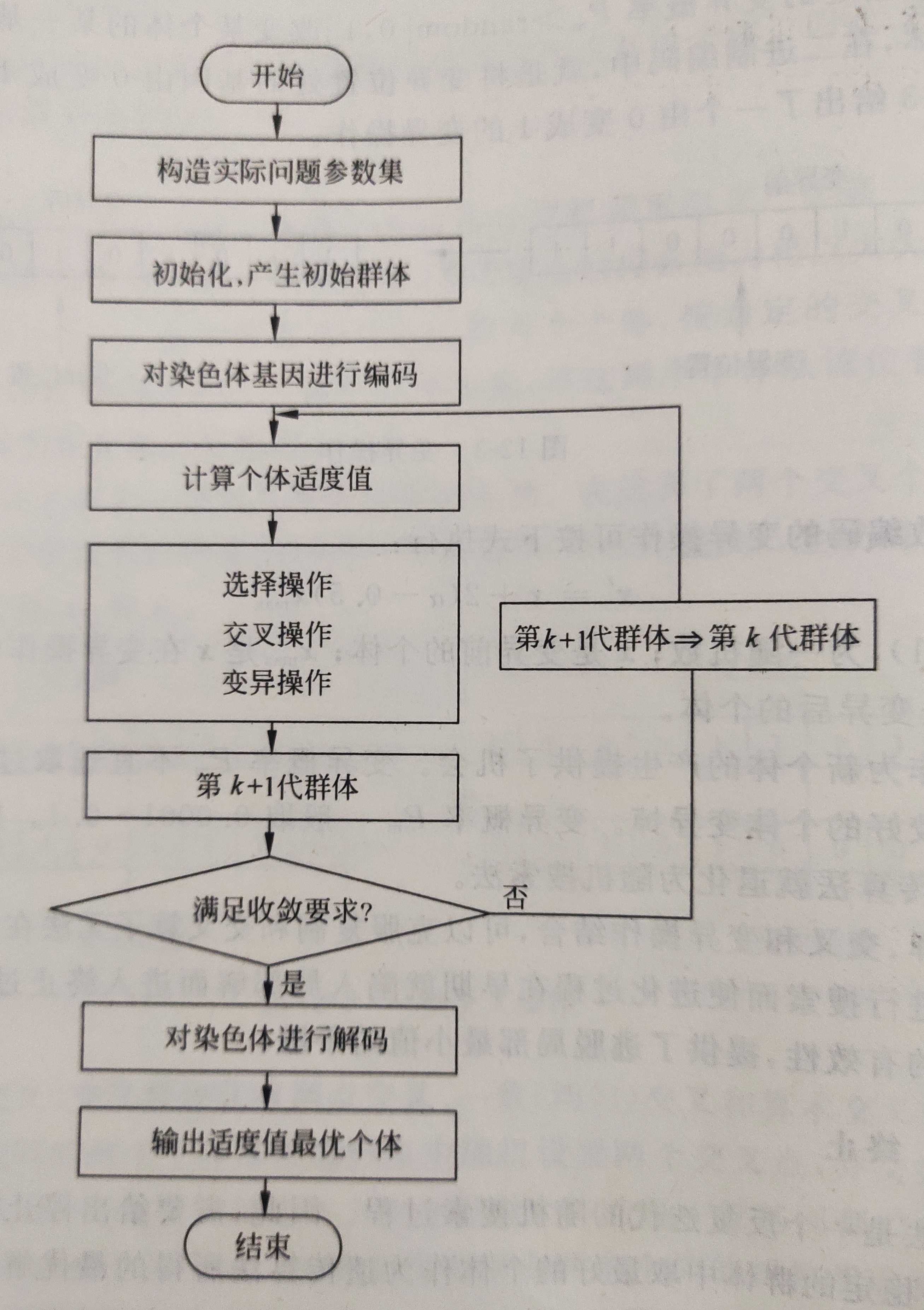
遗传算法流程图
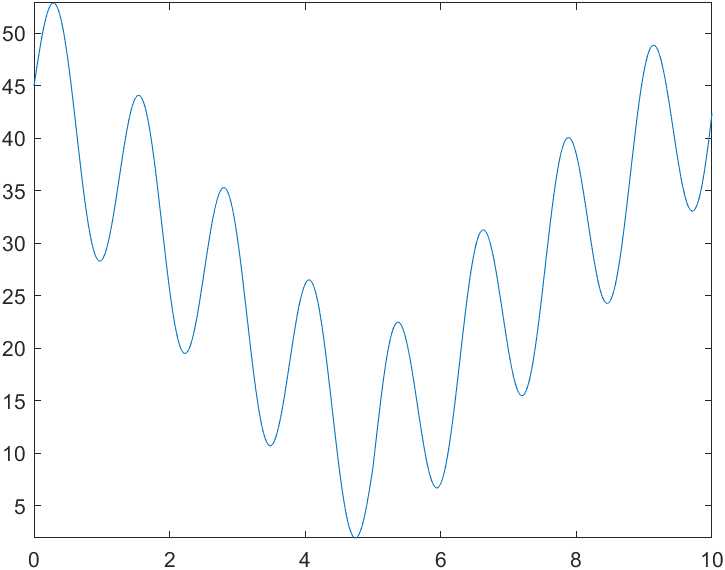
实例:
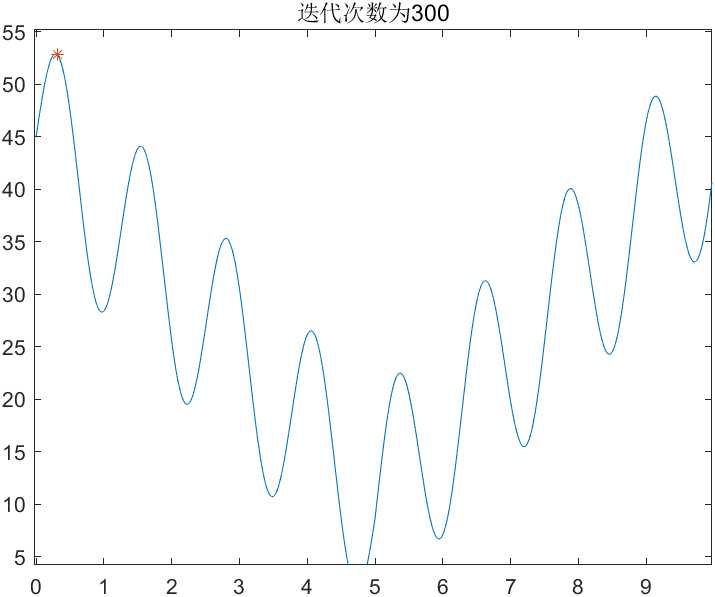
- 求解函数 y = 10 s i n ( 5 x ) + 7 ∗ ∣ x − 5 ∣ + 10 y=10sin(5x)+7*|x-5|+10 y=10sin(5x)+7∗∣x−5∣+10在定义域(0,10)上的最大值
-
主函数
function main() clear; clc; %种群大小 popsize=100; %二进制编码长度 chromlength=10; %交叉概率 pc=0.6; %变异概率 pm=0.001; %初始种群 pop = initpop(popsize,chromlength); %迭代次数 time=300; x=ones(time,1); fitvalue1=ones(time,1); for i=1:time %计算适应度值(函数值) objvalue=cal_objvalue(pop); fitvalue=objvalue; %选择操作 newpop=selection(pop,fitvalue); %交叉操作 newpop=crossover(newpop,pc); %变异操作 newpop=mutation(newpop,pm); %更新种群 pop=newpop; [bestindividual,bestfit]=best(pop,fitvalue); x(i)=binary2decimal(bestindividual); fitvalue1(i)=bestfit; end %寻找最优解 x1=binary2decimal(newpop); y1=cal_objvalue(newpop); %显示最终种群进化后的优解 figure; fplot(@(x)10*sin(5*x)+7*abs(x-5)+10,[0 10]); hold on plot(x1,y1,'*'); title(['迭代次数为' num2str(time)]); %显示每一代的最优解的迭代过程 figure; y=1:time; plot(y,x,'.'); figure; plot(y,fitvalue1,'.'); -
初始种群大小
%初始化种群大小 %输入变量: %popsize:种群大小 %chromlength:染色体长度->转化的二进制长度 %输出变量: %pop:种群 function pop=initpop(popsize,chromlength) pop=round(rand(popsize,chromlength)); -
二进制转换为十进制函数(注意二进制是用矩阵表示的)
%二进制转化为十进制函数 %输入变量: %二进制种群 %输出变量: %十进制数值 function pop2=binary2decimal(pop) [px,py]=size(pop); for i=1:py pop1(:,i)=2.^(py-i).*pop(:,i); end temp=sum(pop1,2); %精度问题,题目定义域长度为10,而10位二进制编码可以表示0~1023 pop2=temp/1023*10; -
适应度函数
%适应度函数 %输入变量:二进制数值 %输出变量:目标函数值 function [objvalue]=cal_objvalue(pop) x=binary2decimal(pop); objvalue=10*sin(5*x)+7*abs(x-5)+10; -
选择函数
%如何选择新的个体 %输入变量:pop二进制种群,fitvalue:适应度值 %输出变量:newpop选择以后的二进制种群 function [newpop]=selection(pop,fitvalue) %构造轮盘 [px,py]=size(pop); totalfit=sum(fitvalue); p_fitvalue=fitvalue/totalfit; p_fitvalue=cumsum(p_fitvalue); ms=sort(rand(px,1)); fitin=1; newin=1; while newin<=px if(ms(newin)<p_fitvalue(fitin)) newpop(newin,:)=pop(fitin,:); newin=newin+1; else fitin=fitin+1; end end -
交叉函数
%交叉变换 %输入变量:pop:二进制父代种群数,pc:交叉概率 %输出变量:newpop:交叉后的种群数 function [newpop]=crossover(pop,pc) [px,py]=size(pop); newpop=ones(size(pop)); for i=1:2:px-1 if(rand<pc) cpoint=round(rand*py); newpop(i,:)=[pop(i,1:cpoint),pop(i+1,cpoint+1:py)]; newpop(i+1,:)=[pop(i+1,1:cpoint),pop(i,cpoint+1:py)]; else newpop(i,:)=pop(i,:); newpop(i+1,:)=pop(i+1,:); end end -
变异函数
%变异 %输入变量:pop:二进制种群,pm:变异概率 %输出变量:newpop变异后的种群 function [newpop]=mutation(pop,pm) [px,py]=size(pop); newpop=ones(size(pop)); for i=1:px newpop(i,:)=pop(i,:); if(rand<pm) mpoint=round(rand*py); if mpoint<=0 mpoint=1; end if newpop(i,mpoint)==0 newpop(i,mpoint)=1; else newpop(i,mpoint)=0; end end end -
取最优值函数
%求最优适应度函数 %输入变量:pop:种族,fitvalue:种群适应度 %输出变量:bestindividual:最佳个体,bestvalue:最佳适应度值 function [bestindividual,bestfit]=best(pop,fitvalue) [px,py]=size(pop); bestindividual=pop(1,:); bestfit=fitvalue(1); for i=2:px if bestfit<fitvalue(i) bestindividual=pop(i,:); bestfit=fitvalue(i); end end
- 执行结果
-
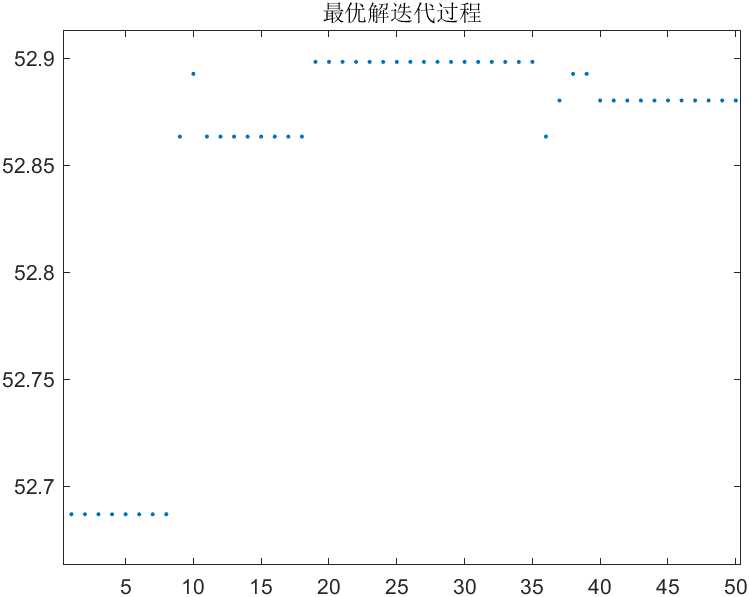
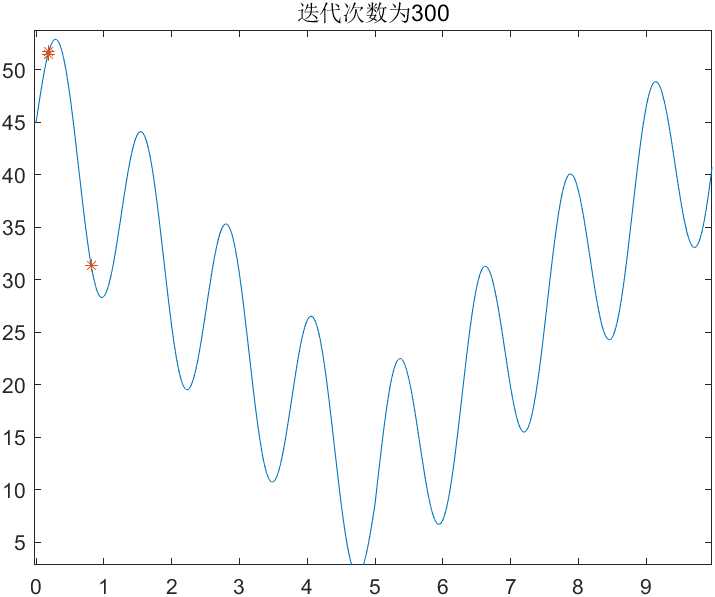
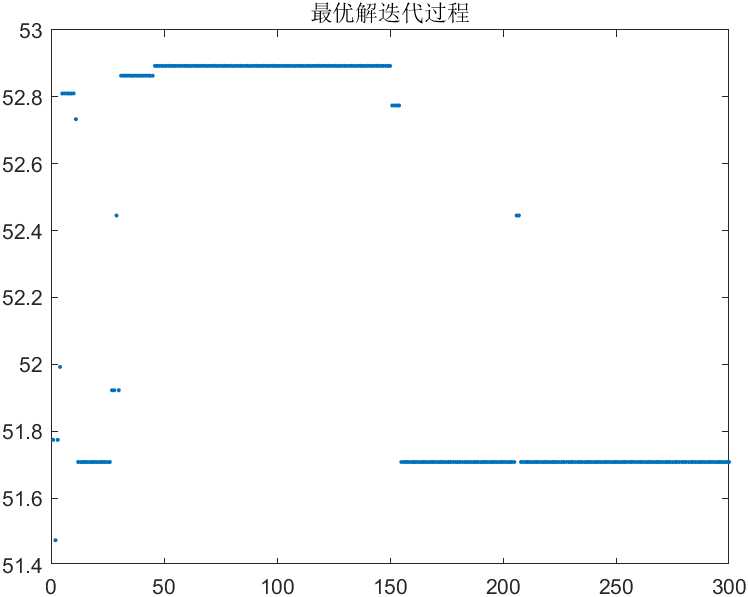
第一次执行,迭代300次
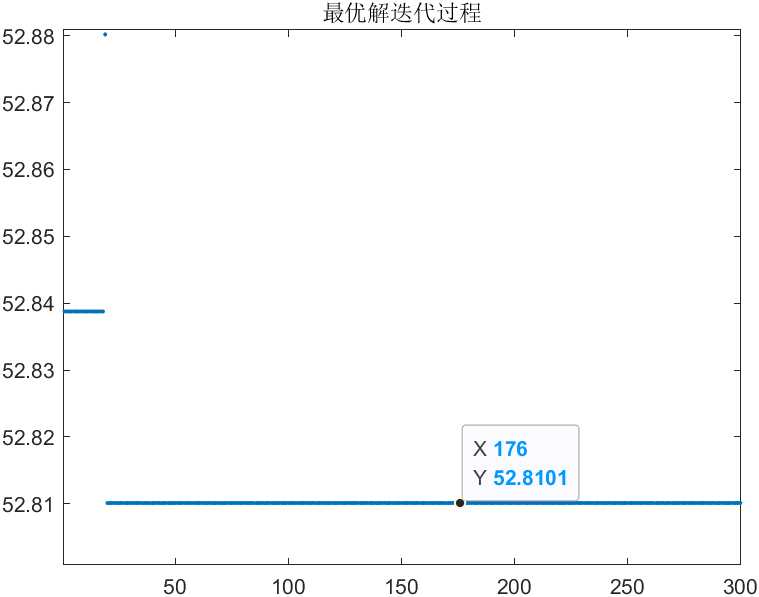
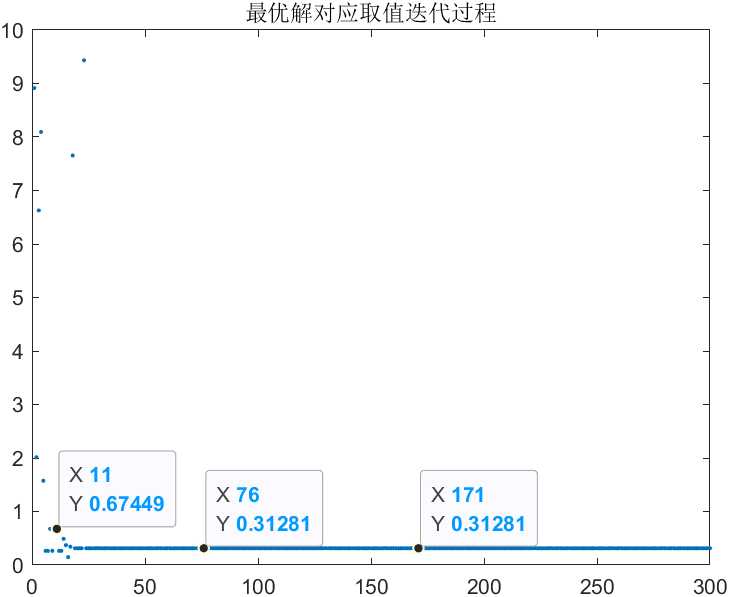
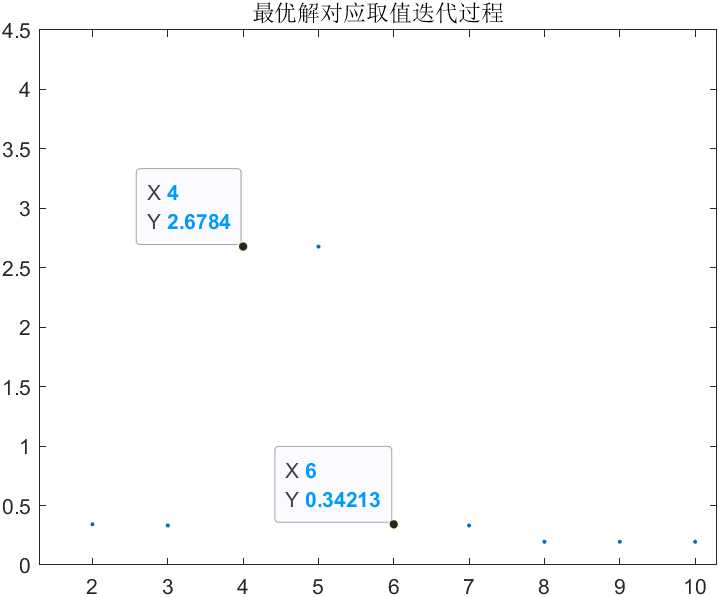
纵坐标对应X取值
-
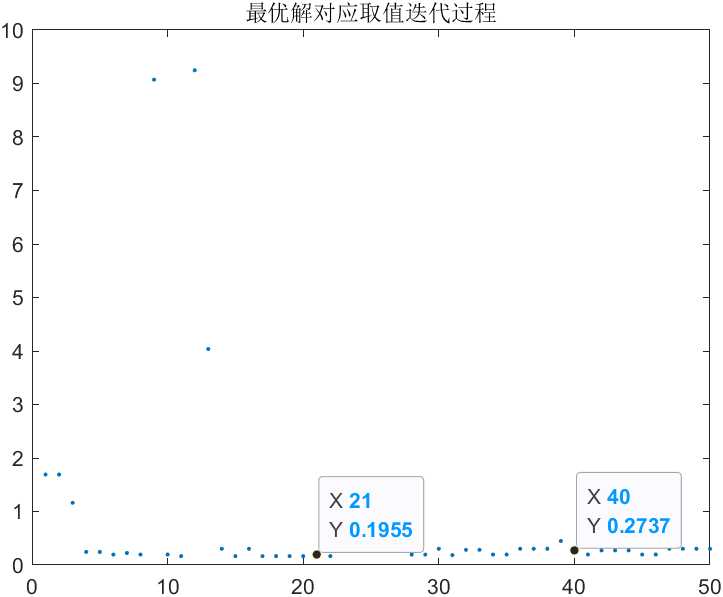
第二次执行,迭代300次
纵坐标对应X取值 -
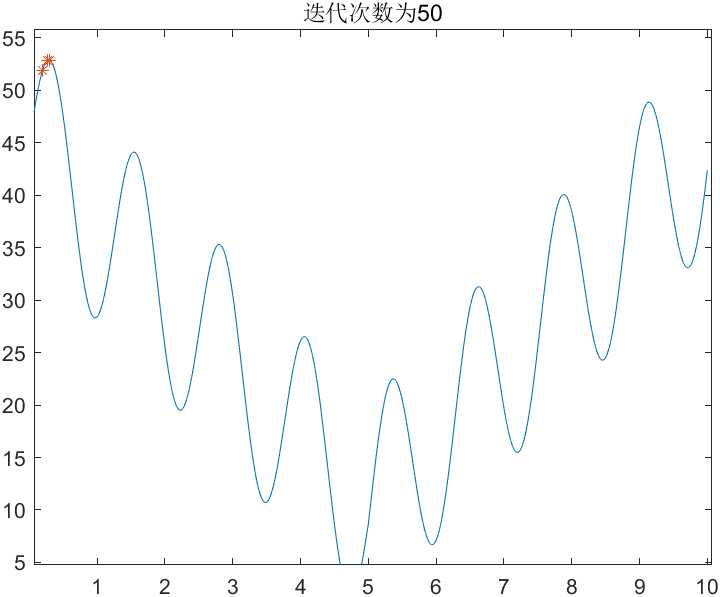
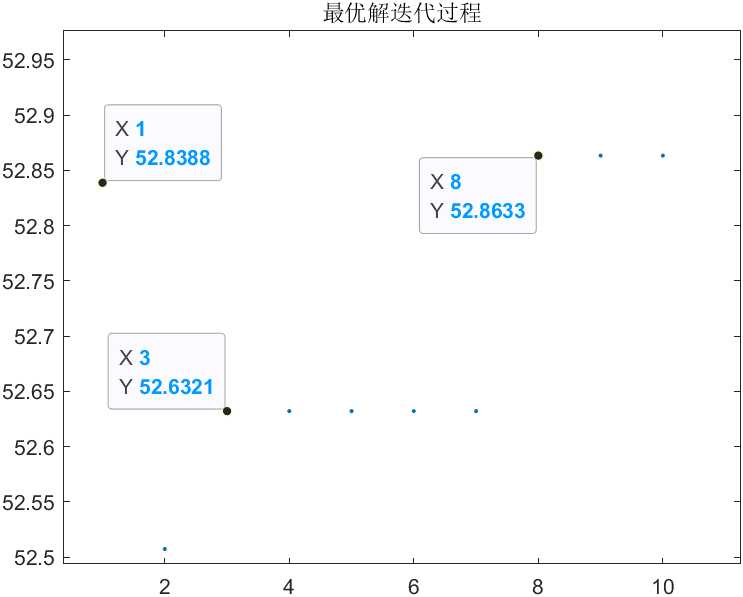
第三次执行,迭代50次
纵坐标对应X取值 -
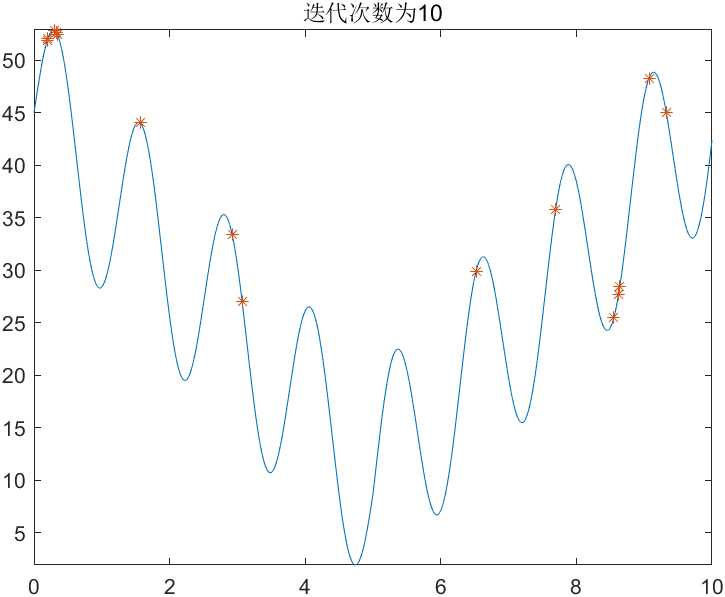
第四次执行,迭代10次
纵坐标对应X取值
-
物竞天择,适者生存
今天的文章遗传算法及matlab简单实现分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/33049.html

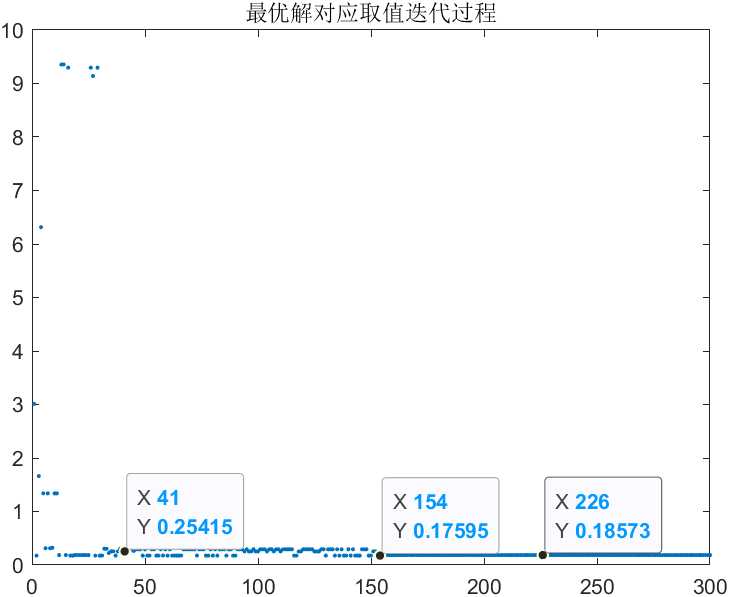 纵坐标对应X取值
纵坐标对应X取值