matlab编写的流体计算和传热

% Twodimensional heat conduction
% Finite Volume Method
% SOR
clear all;
x=[];y=[];T=[];Told=[];Su=[];Sp=[];ap=[];ae=[];aw=[];as=[];an=[];
great = 1.e20;
lambda = 10; % thermal conductivity
alfa = 10; % heat transfer coefficient
dt = great; % Time step. If great stedy state
density = 6000;% density
cp = 500;% heat capacity
Lx = 0.12; % length x-direction
Ly = 0.12; % length y -direction
Tfluid = 20; % Fluid temperature
Tinit = 50; % Initial guess and top- and bottom tempearature
%cv_x = input(‘Number of CVs in x-direction = ‘)
%cv_y = input(‘Number of CVs in y-direction = ‘)
cv_x=10;cv_y=10;
ni = cv_x+2; % grid points x-direction
nj = cv_y+2; % grid points y-direction
dx = Lx/cv_x;
dy = Ly/cv_y;
x(1) = 0;
x(2)=dx/2;
for i = 3:ni-1
   x(i)=x(i-1)+dx;
end;
x(ni)=Lx;
y(1) = 0;
y(2)=dy/2;
for j = 3:nj-1
   y(j)=y(j-1)+dy;
end
y(nj)=Ly;
% Initial values and coefficients
for i = 1:ni
  for j = 1:nj
    T(i,j) = Tinit;  %Initial temperature
    Told(i,j) = Tinit;
    T(i,1) = 50;
    T(i,nj) = 50;
    Su(i,j)=0;       %Initial indendendent source term
    Sp(i,j)=0;       %Initial dependent source term
    ae(i,j) = lambda*dy/dx;
    aw(i,j) = lambda*dy/dx;
    an(i,j) = lambda*dx/dy;
    as(i,j) = lambda*dx/dy;
    dV = dx*dy;
    ap0 = density*cp*dV/dt;
    if i==2  % convective heat transfer boundary
       Su(i,j) = Tfluid/(1/alfa+dx/(2*lambda))*dy/dV;
       Sp(i,j) = -1/(1/alfa+dx/(2*lambda))*dy/dV;
       aw(i,j) = 0;
    end;
    if i==ni-1 % insulated boundary
       ae(i,j) = 0;
    end
    if j==2 % bottom boundary, given temperature
       as(i,j)=2*lambda*dx/dy;
    end   
    if j==nj-1 % top boundary, given temperature
       an(i,j)=2*lambda*dx/dy;
    end   
    ap(i,j) = ae(i,j)+aw(i,j)+an(i,j)+as(i,j)-Sp(i,j)*dV+ap0;
  end;
end;
%%%%%%%%%%%
maxres = 1.0e-6;
maxit = 100;
time=0;
maxtime=100;
s=(cos(pi/cv_x)+(dx/dy)^2*cos(pi/cv_y))/(1+(dx/dy)^2);
omega =2/(1+sqrt(1-s^2));omega=1;
while (time < (maxtime+dt/2))
 Told=T;  
 sumres = 1;
 counter = 0;
 while (sumres>maxres&counter<maxit)
  sumres = 0;
  for i = 2:ni-1
   for j = 2:nj-1
    T(i,j)=omega*(ae(i,j)*T(i+1,j)+aw(i,j)*T(i-1,j)+an(i,j)*T(i,j+1)…
       +as(i,j)*T(i,j-1)+Su(i,j)*dV+ap0*Told(i,j))/ap(i,j)+(1-omega)*T(i,j);
    res =  abs(ap(i,j)*T(i,j)-(ae(i,j)*T(i+1,j)+aw(i,j)*T(i-1,j)+…
      an(i,j)*T(i,j+1)+as(i,j)*T(i,j-1)+Su(i,j)*dV+ap0*Told(i,j)));
    sumres=sumres+res;
   end;
  end;
  for i = 2:ni-1
   for j = 2:nj-1
    res =  abs(ap(i,j)*T(i,j)-(ae(i,j)*T(i+1,j)+aw(i,j)*T(i-1,j)+…
      an(i,j)*T(i,j+1)+as(i,j)*T(i,j-1)+Su(i,j)*dV+ap0*Told(i,j)));
    sumres=sumres+res;
   end;
  end

  sumerr=sumres
  counter = counter + 1
 end;
 time = time +dt;
end; 
% Calculate boundary values
 for j = 2:nj-1
   T(1,j)=(alfa*Tfluid+lambda/(dx/2)*T(2,j))/(alfa+lambda/(dx/2));
   T(ni,j) = T(ni-1,j);
end;   
%
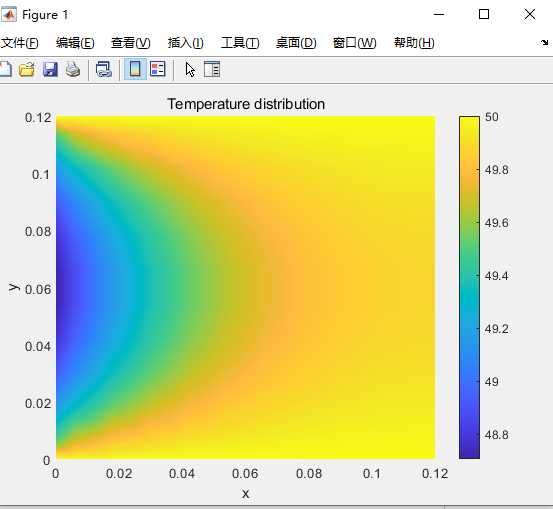
pcolor(x,y,T’);shading interp;xlabel(‘x’);ylabel(‘y’);title(‘Temperature distribution’);colorbar;
%

D144

今天的文章matlab编写的流体计算和传热分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。