概况
快速排序(Quick sort)是对冒泡排序的一种改进。快速排序由C. A. R. Hoare在1960年提出。
算法思路
通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序算法通过多次比较和交换来实现排序,其排序流程如下:
1、首先设定一个分界值,通过该分界值将数组分成左右两部分。
2、将大于或等于分界值的数据集中到数组右边,小于分界值的数据集中到数组的左边。此时,左边部分中各元素都小于或等于分界值,而右边部分中各元素都大于或等于分界值。
3、然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
4、重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当左、右两个部分各数据排序完成后,整个数组的排序也就完成了。
概括来说为 挖坑填数 + 分治法。
图解算法
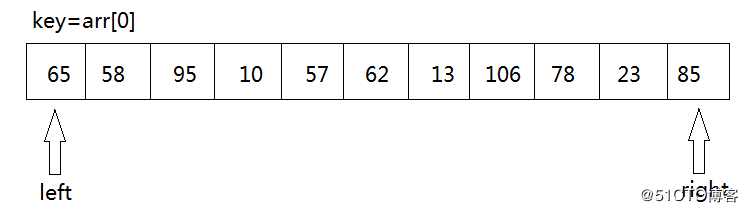
快速排序主要有三个参数,left 为区间的开始地址,right 为区间的结束地址,Key 为当前的开始的值。
我们从待排序的记录序列中选取一个记录(通常第一个)作为基准元素(称为key)key=arr[left],然后设置两个变量,left指向数列的最左部,right 指向数据的最右部。
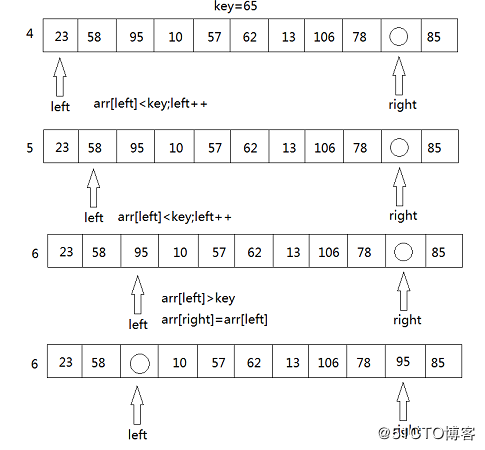
第一步
key 首先与 arr[right] 进行比较,如果 arr[right]<key,则arr[left]=arr[right]将这个比key小的数放到左边去,如果arr[right]>key则我们只需要将right–,right–之后,再拿arr[right]与key进行比较,直到arr[right]<key交换元素为止。
第二步
如果右边存在arr[right]<key的情况,将arr[left]=arr[right],接下来,将转向left端,拿arr[left ]与key进行比较,如果arr[left]>key,则将arr[right]=arr[left],如果arr[left]<key,则只需要将left++,然后再进行arr[left]与key的比较。
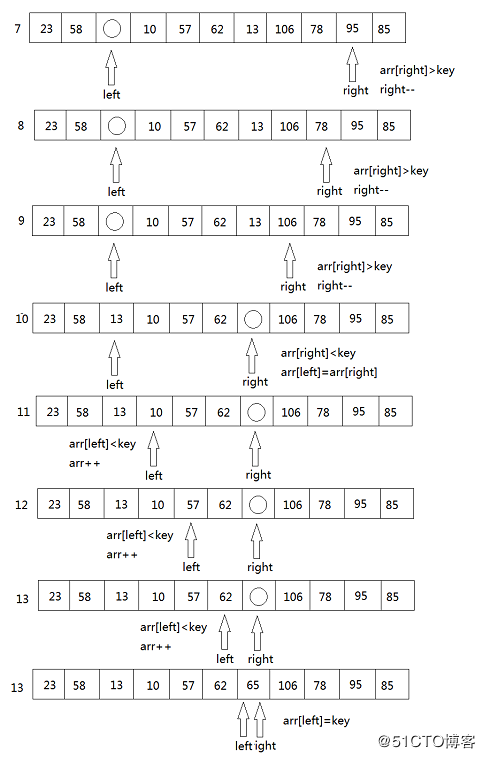
第三步
然后再移动right重复上述步骤。
第四步
最后得到 {23 58 13 10 57 62} 65 {106 78 95 85},再对左子数列与右子数列进行同样的操作。最终得到一个有序的数列。
{23 58 13 10 57 62} 65 {106 78 95 85}
{10 13} 23 {58 57 62} 65 {85 78 95} 106
10 13 23 57 58 62 65 78 85 95 106
动画展示
我们借用五分钟学算法的gif动图,感谢五分钟学算法。
- 首先,操作数列中的所有数字
- 在所有数字中选择一个数字作为排序的基准(pivot), pivot 通常是随机选择的,在这里为了演示方便,我们选择最右边的数字作为 pivot
- 选取好 pivot 后,在操作数列中选择最左边的数字标记为 左标记 ,最右边的数字标记为 右标记
- 将左边的标记向右移动
- 当 左标记 达到超过 pivot 的数字时,停止移动
- 在这里,8 > 6 ,所以停止移动
- 然后将右边的标记向左移动
- 当 右标记 达到小于 pivot 的数字时,停止移动
- 在这里,4 > 6 ,所以停止移动
- 当左右标记停止时,更改标记的数字
- 因此,左标记 的作用是找到一个大于 pivot 的数字,右标记 的作用是找到一个小于 pivot 的数字
- 通过交换数字,可以在数列的左边收集小于 pivot 的数字集合,右边收集大于 pivot 的数字集合
- 交换之后,继续移动 左标记
- 在这里,9 > 6 ,所以停止移动
- 然后将右边的标记向左移动
- 当 右标记 碰撞到 左标记 时也停止移动
- 如果左右侧的标记停止时,并且都在同一个位置,将这个数字和 pivot 的数字交换
- 这就完成了第一次操作
- 小于 6 的都在 6 的左侧,大于 6 的都在 6 的右侧
- 然后递归对这分成的两部分都执行同样的操作
- 完成 快速排序
算法性能
时间复杂度
理想情况
如果足够理想,那我们期望每次都把数组都分成平均的两个部分,如果按照这样的理想情况分下去,我们最终能得到一个完全二叉树。如果排序 n 个数字,那么这个树的深度就是
T(n) ≤ 2T(n/2) + n,T(1) = 0
T(n) ≤ 2(2T(n/4)+n/2) + n = 4T(n/4) + 2n
T(n) ≤ 4(2T(n/8)+n/4) + 2n = 8T(n/8) + 3n
......
T(n) ≤ nT(1) + (log2n)×n = O(nlogn) 最坏情况
而在最坏的情况下,这个树是一个完全的斜树,只有左半边或者右半边。这时候我们的比较次数就变为
空间复杂度
原地排序
原地快排的空间占用是递归造成的栈空间的使用,最好情况下是递归
n-1 次,所以空间复杂度是
非原地排序
对于非原地排序,每次递归都要声明一个总数为n的额外空间,所以空间复杂度变为原地排序的n倍,即最好情况下

稳定性
不稳定。
代码实现
C和C++
void QuickSort(int array[], int low, int high) {
int i = low;
int j = high;
if(i >= j) {
return;
}
int temp = array[low];
while(i != j) {
while(array[j] >= temp && i < j) {
j--;
}
while(array[i] <= temp && i < j) {
i++;
}
if(i < j) {
swap(array[i], array[j]);
}
}
//将基准temp放于自己的位置,(第i个位置)
swap(array[low], array[i]);
QuickSort(array, low, i - 1);
QuickSort(array, i + 1, high);
}Java
public static int[] qsort(int arr[],int start,int end) {
int pivot = arr[start];
int i = start;
int j = end;
while (i<j) {
while ((i<j)&&(arr[j]>pivot)) {
j--;
}
while ((i<j)&&(arr[i]<pivot)) {
i++;
}
if ((arr[i]==arr[j])&&(i<j)) {
i++;
} else {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
}
if (i-1>start) arr=qsort(arr,start,i-1);
if (j+1<end) arr=qsort(arr,j+1,end);
return (arr);
} Python
def swap(arr, i, j):
arr[i], arr[j] = arr[j], arr[i]
def partition(arr, left, right):
pivot = left
index = pivot+1
i = index
while i<=right:
if arr[i]<arr[pivot]:
swap(arr, i, index)
index+=1
i+=1
swap(arr, pivot, index-1)
return index-1
def quickSort(arr, left=None, right=None):
left = 0 if not isinstance(left, (int, float)) else left
right = len(arr)-1 if not isinstance(right, (int, float)) else right
if left < right:
partitionIndex = partition(arr, left, right)
quickSort(arr, left, partitionIndex-1)
quickSort(arr, partitionIndex+1, right)
return arr今天的文章排序——快速排序(Quick sort)分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/33246.html