曲线拟合
插值与拟合的区别:
- 实现方法:插值要求曲线穿过样本点,而拟合不需要穿过样本点,只要求总体误差最小。
- 结果形式:插值是分段逼近样本点,没有同一的逼近函数;函数拟合则用一个函数去逼近,有完整的表达式。
- 侧重点:插值可以用于估计区间内某些点对应的函数值;拟合不仅可以估计区间内的点,也可以预测区间外的点。
- 应用场合:插值多用于精确数据集;拟合多用于统计数据集。
polyfit函数用于一元多次曲线拟合(亦多项式拟合),形如: y = a x 5 + b x 4 + c x 3 + d x 2 + e x + f y=ax^5+bx^4+cx^3+dx^2+ex+f y=ax5+bx4+cx3+dx2+ex+f,我们已知 x x x、 y y y样本数据,利用此函数求解参数(系数) a a a、 b b b、 c c c、 d d d、 e e e、 f f f。
regress函数用于一元或多元线性回归(拟合),形如: y = a x 1 + b x 2 + c x 3 + d x 4 + e y=ax_1+bx_2+cx_3+dx_4+e y=ax1+bx2+cx3+dx4+e,我们已知 x 1 x_1 x1、 x 2 x_2 x2、 x 3 x_3 x3、 x 4 x_4 x4、 y y y样本数据,利用此函数求解参数(系数) a a a、 b b b、 c c c、 d d d、 e e e。
polyfit函数
调用格式:
-
[P,S,mu]=polyfit(X,Y,m)
-
[P,S]=polyfit(X,Y,m)
-
P=polyfit(X,Y,m)
参数解释:
根据样本数据X和Y,产生一个m次多项式系数向量P及其在采样点误差数据S,mu是一个二元向量,mu(1)是mean(X),而mu(2)是std(X)。
x=0: 0.1: 1;
y=[-0.447, 1.978, 3.11, 5.25, 5.02, 4.66, 4.01, 4.58, 3.45, 5, 35];
p = polyfit(x, y, 3) % 三次多项式拟合
xx = 0: 0.01 : 1;
yy = polyval(p, xx) ; % 根据系数向量p计算在xx点处的函数值
plot(xx, yy, '-b', x, y, 'markersize', 20)
当还需要进行线性回归分析时,可以再利用corrcoef函数获取相关系数。
regress函数
在matlab的regress函数中置信区间bint、rint以及stats后面三个值全都为无穷大,这说明数据不服从线性关系,应考虑用非线性拟合函数来拟合。
调用格式:
- [B,BINT,R,RINT,STATS] = regress(Y,X)
- [B,BINT,R,RINT] = regress(Y,X)
- [B,BINT,R] = regress(Y,X)
- [B,BINT] = regress(Y,X)
- B = regress(Y,X)
参数解释:
调用该函数要保证目标函数的形式已知,比如目标函数为: y = a x 1 + b x 2 + c x 3 + d x 4 + e y=ax_1+bx_2+cx_3+dx_4+e y=ax1+bx2+cx3+dx4+e,或者是 y = a x 1 2 + b x 2 2 + c x 1 + d x 2 + e x 1 × x 2 + f y = ax_1^2+bx_2^2+cx_1+dx_2+ex_1×x_2+f y=ax12+bx22+cx1+dx2+ex1×x2+f这样的多元多次多项式。传入参数,调用该函数后得到拟合出的系数值。
- x是一个矩阵。矩阵的每一个样本,即行数等于样本数,每个样本的每一列表示该样本在多项式中每一项除去系数之外的值。
- y是一个列向量。向量维度与矩阵行数一致,同为样本数,每一个值表示每个样本对应的函数值。
该函数根据多个样本的 x i x_i xi和 y y y拟合出多项式的系数。
返回值解释:
- B:回归系数,即未知参数,B(1)为常数项,B(2~……)依次为X每一列(从第二列起)对应的项的系数;
- BINT:回归系数的置信区间。(置信区间:当给出某个估计值的95%置信区间为[a, b]时,可以理解为我们有95%的信心可以说样本的平均值介于a到b之间,而发生错误的概率为5%)
- R:残差(残差是指观测值与预测值(拟合值)之间的差,即是实际观察值与回归估计值的差)
- RINT:残差的置信区间。
- STATS:用于检验回归模型的统计量。有4个数值:判定系数 R 2 R^2 R2(度量拟合优度的统计量,R²的值越接近1,说明回归直线对观测值的拟合程度越好), F F F统计量观测值,检验的 p p p的值( p < 0.05 p<0.05 p<0.05时回归模型成立),误差方差的估计。
x1=[3.91 6.67 5.33 5.56 6.12 7.92 5.82 5.5 5.59 6.12 6.68 6.93]';
x2=[9.43 14.5 15.8 19.8 17.4 23.8 31.6 37.1 36.4 32.2 36.6 41.3]';
X=[ones(12,1), x1, x2];
Y=[280 338 405 432 452 582 596 602 606 621 629 656]';
[b,bint,r,rint,stats] = regress(Y,X)
rcoplot(r,rint) % 绘制残差图
残差图:残差图中圆圈是每个数据点的实际残差,横线区间是残差置信区间,置信区间穿过原点说明方程拟合的很好;未通过原点,可视为异常点,比如上图中显示第二组数据未通过原点,因此第二组数据拟合结果较差。
之后可将第二组数据去除后再次进行拟合,得到的结果更为准确。
%% 目标函数:y=Ax1^2+Bx2^2+Cx1+Dx2+Ex1*x2+F (这是一个二次函数,两个变量,大写的字母是常数)
format long;
y=[7613.51 7850.91 8381.86 9142.81 10813.6 8631.43 8124.94 9429.79 10230.81 10163.61 9737.56 8561.06 7781.82 7110.97]';
x1=[7666 7704 8148 8571 8679 7704 6471 5870 5289 3815 3335 2927 2758 2591]';
x2=[16.22 16.85 17.93 17.28 17.23 17 19 18.22 16.3 13.37 11.62 10.36 9.83 9.25]';
X=[ones(size(y)) x1.^2 x2.^2 x1 x2 x1.*x2]; % 构造X矩阵!!!
[b,bint,r,rint,stats] = regress(y,X)
结果如下:
b =
1.0e+04 *
-1.353935450267780
0.000000089381408
-0.005811190715467
-0.000605427789545
0.479983626458515
-0.000037869040292
bint =
1.0e+04 *
-2.621944842897225 -0.085926057638335
0.000000034253753 0.000000144509063
-0.027588831662544 0.015966450231609
-0.001309493882546 0.000098638303455
0.119564693553897 0.840402559363132
-0.000105954336341 0.000030216255756
r =
1.0e+02 *
-4.397667358984126
-2.361417286008764
-1.434643909138249
-5.904203974279353
7.511701773844997
5.570806699070599
-2.447861341816779
0.494622057474844
6.376995507987613
-6.789520765534544
2.744335484633611
1.578124015815701
-0.803533566911865
-0.137737336155596
rint =
1.0e+03 *
-1.219619853471144 0.340086381674319
-1.426253867770768 0.953970410569015
-0.919089416302223 0.632160634474573
-1.568776909577359 0.387936114721488
0.111430783412043 1.390909571356956
-0.533006860832905 1.647168200647025
-1.168898277755904 0.679326009392548
-0.977546779130818 1.076471190625786
-0.398546999643731 1.673946101241254
-1.439044988776064 0.081140835669156
-0.919162439561023 1.468029536487746
-1.088788822632291 1.404413625795431
-1.271236485719865 1.110529772337492
-1.017369947314269 0.989822480083149
stats =
1.0e+05 *
0.000008444011951 0.000086828553270 0.000000043344434 3.162249735298930
参数X的第一列为全1列向量,从第二列开始分别为每一个系数对应项对应样本数据构成的列向量,本题的目标函数是个二元二次的,由于regress函数只能解决线性问题,因此我们将 x 1 2 x_1^2 x12看作第一项, x 2 2 x_2^2 x22看作第二项, x 1 x_1 x1看作第三项, x 2 x_2 x2看作第四项, x 1 x 2 x_1x_2 x1x2看作第五项,这样就相当于一个五元一次的目标函数了。
b为对应的参数 b(1)为F(最后那个常数项) ,b(2)为A(第一个参数),b(3)为B,b(4)为C,b(4)为D,b(5)为E。
bint为b的95%置信区间。
stats的第三个参数为F检测的p值,p值很小(p<0.05),说明拟合模型有效。
应用
已知随机性参数与多样性度量和与收敛性度量之间的关系如下表,多样性与收敛性同样重要,问选取随机参数的平衡点。
表1 随机性参数与多样性度量之间的关系
| x | 0.03 | 0.06 | 0.09 | 0.12 | 0.15 | 0.18 | 0.21 | 0.24 | 0.27 | 0.3 |
| y1 | 0.01 | 0.01 | 0.02 | 0.03 | 0.06 | 0.07 | 0.13 | 0.17 | 0.25 | 0.37 |
表2 随机性参数与收敛性度量之间的关系
| x | 0.03 | 0.06 | 0.09 | 0.12 | 0.15 | 0.18 | 0.21 | 0.24 | 0.27 | 0.3 |
| y1 | 0.85 | 0.76 | 0.68 | 0.62 | 0.54 | 0.52 | 0.5 | 0.49 | 0.48 | 0.47 |
x=0.03:0.03:0.3;
y1=[0.01,0.01,0.02,0.03,0.06,0.07,0.13,0.17,0.25,0.37];
y2=[0.85,0.76,0.68,0.62,0.56,0.52,0.49,0.46,0.43,0.39];
plot(x,y1,'*',x,y2,'o');
legend('多样性','收敛性')
问题分析:
随机性参数的增长导致多样性增加,收敛性降低;两者同等重要,则取平衡点;平衡点最佳位置是多样性和收敛性相等的地方。
解决方案:
第一步:分别对多样性和收敛性进行拟合,得到拟合曲线。
第二步:找到两曲线的交点。
p1=polyfit(x,y1,2);
p2=polyfit(x,y2,2);
p=p1-p2;
xi=roots(p); % -1.14148334023966 0.316172995412073
xj=0:0.03:0.36;
yj1=polyval(p1,xj);
yj2=polyval(p2,xj);
yi=polyval(p1,xi(2))
plot(x,y1,'*',x,y2,'o',xj,yj1,xj,yj2,xi(2),yi,'rp');
lsqlin函数
由于这个函数用的比较少,网上相关资料也就比较少,因此下面部分思路比较主观。
具有边界或线性约束的线性最小二乘求解器。
求解以下形式的最小二乘曲线拟合问题:
这里我就举个最简单的例子:
%% y=ax^2+bxsinx+cx^3
xdata = [3.6,7.7,9.3,4.1,8.6,2.8,1.3,7.9,10.0,5.4];
ydata = [16,150.5,260.1,22.5,206.5,9.9,2.7,165.5,325.0,54.5];
C =[ xdata'.^2, xdata'.*sin(xdata'),xdata'.^3]; d = ydata';
[x, resnorm, residual] = lsqlin(C, d);
%% 绘图
xi = 0:0.1:11;
f = @(c, x) c(1).*x.^2 + c(2).*x.*sin(x) + c(3).*x.^3;
plot(xdata, ydata, '*', xi, f(x, xi))
函数的缺点:当上边界(ub)或下边界(lb)或Aeq或beq中的限制是对非多项式项进行的时,这些限制矩阵是很难构造出来的。比如,上面的代码中将 x 2 x^2 x2、 x s i n x xsinx xsinx、 x 3 x^3 x3分别看作第一、二、三项,因此约束条件矩阵也必须是对这三项的约束,但是若题目只给出了对 x x x的限制呢?若题目只给出了对 x e x l g x xe^xlgx xexlgx的限制呢?很难转化成对每一项的约束条件。
不知道如何处理”某些项有上下界的限制,而其他项没有上下界的限制“的情况。
对于这个函数所知甚少,且网上相关内容太少了。
lsqcurvefit函数
最小二乘法求解非线性拟合问题!!!
调用格式:
-
x = lsqcurvefit(fun,x0,xdata,ydata)
-
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub)
-
x = lsqcurvefit(fun,x0,xdata,ydata,lb,ub,options)
-
[x,resnorm,residual,exitflag] = lsqcurvefit(…)
参数解释:
- x0为待求参数(初始解向量),初始变量的选取影响最终解
- xdata,ydata为用于拟合的数据
- lb、ub为解向量的下界和上界lb≤x≤ub,若没有指定界,则lb=[ ],ub=[ ]
- fun为待拟合函数,计算x处拟合函数值,其参数一般有两类,一类是目标函数的参数,一类是目标函数的未知数
返回值解释:
- x为待求参数向量
- resnorm=sum ((fun(x,xdata)-ydata).^2),即在x处残差的平方和
- residual=fun(x,xdata)-ydata,即在x处的残差
- exitflag为终止迭代的条件
%% y=tcos(kx)e^(wx)
x=[0,0.4,1.2,2,2.8,3.6,4.4,5.2,6,7.2,8,9.2,10.4,11.6,12.4,13.6,14.4,15]';
y=[1,0.85,0.29,-0.27,-0.53,-0.4,-0.12,0.17,0.28,0.15,-0.03,-0.15,-0.07,0.059,0.08,0.032,-0.015,-0.02]';
f= @(c,x) c(1)*cos(c(2)*x).*exp(c(3)*x);
c0= [0 0 0];
[c, fval]= lsqcurvefit(f, c0, x, y);
xx=0:0.1:20;
yy=f(c, xx);
plot(x, y, 'r*', xx, yy, 'b-');
disp(c);
注意:这里定义的函数比较特别,待拟合参数也要作为函数的参数传到函数中,我们将待拟合参数视为一个向量传入函数的目的是使函数的形式更加简洁。
xdata = [3.6,7.7,9.3,4.1,8.6,2.8,1.3,7.9,10.0,5.4];
ydata = [16,150.5,260.1,22.5,206.5,9.9,2.7,165.5,325.0,54.5];
c0=[ 0 0 0];
f_h=@(c, x) c(1)*x.^2 + c(2)*x.*sin(x) + c(3)*x.^3;
[c, resnorm, r]=lsqcurvefit(f_h, c0, xdata, ydata);
%% 绘图
xx=0:0.1:11;
yy=f_h(c, xx);
plot(xdata, ydata, 'r*', xx, yy, 'b-');
disp(c);
fittype函数和fit函数
自行学习,用的较少,需要时直接百度即可(对于打比赛的而言)。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/34463.html

![【Matlab】曲线拟合插图1 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HfdDYeiK-1655004670298)(C:\Users\23343\AppData\Roaming\Typora\typora-user-images\image-20210905121325482.png)]](https://img.mushiming.top/app/bianchenghao_cn/33473e152ea44d10ba79a22ed0cee0bc.jpg)
![【Matlab】曲线拟合插图3 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1Y5opgw0-1655004670300)(C:\Users\23343\AppData\Roaming\Typora\typora-user-images\image-20210905133501687.png)]](https://img.mushiming.top/app/bianchenghao_cn/9fd23f9d5df446e5a76ac6c56268e86b.jpg)
![【Matlab】曲线拟合插图5 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aJvIw8H0-1655004670300)(C:\Users\23343\AppData\Roaming\Typora\typora-user-images\image-20210905151252383.png)]](https://img.mushiming.top/app/bianchenghao_cn/0e6db91b562a47b6a4af7c82d514f466.jpg)
![【Matlab】曲线拟合插图7 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XHuzPPTI-1655004670301)(C:\Users\23343\AppData\Roaming\Typora\typora-user-images\image-20210905170755125.png)]](https://img.mushiming.top/app/bianchenghao_cn/d677950cad2d4309a7d8f2da1832f06e.jpg)
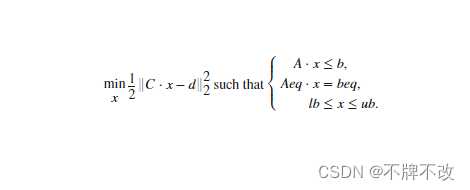
![【Matlab】曲线拟合插图11 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-iTZuCS8E-1655004670301)(C:\Users\23343\AppData\Roaming\Typora\typora-user-images\image-20210905193249034.png)]](https://img.mushiming.top/app/bianchenghao_cn/31c24bb29c274e7db2f9d2882322ea42.jpg)
![【Matlab】曲线拟合插图13 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Qb3dbz25-1655004670301)(C:\Users\23343\AppData\Roaming\Typora\typora-user-images\image-20210905200611657.png)]](https://img.mushiming.top/app/bianchenghao_cn/23e637343a144fbcbc8ef561a5d3e8f9.jpg)
![【Matlab】曲线拟合插图15 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EYS2XXhz-1655004670302)(C:\Users\23343\AppData\Roaming\Typora\typora-user-images\image-20210905201055326.png)]](https://img.mushiming.top/app/bianchenghao_cn/e1609e23cdd449c6a84e5aaf1019213f.jpg)