float类型表示方式及范围深度解析

float类型的值以4个字节表示，共32bit,根据IEEE754标准，float类型使用1位做符号位，8位做指数位，23位做尾数位，格式如下：

整个浮点数可表示为： $\times t \times 2^{i}$ ，其中 $s$ 为符号位-1或1， $t$ 为尾数， $i$ 为指数

下面将三个部分分别进行介绍

符号位：

0表示正，1表示负

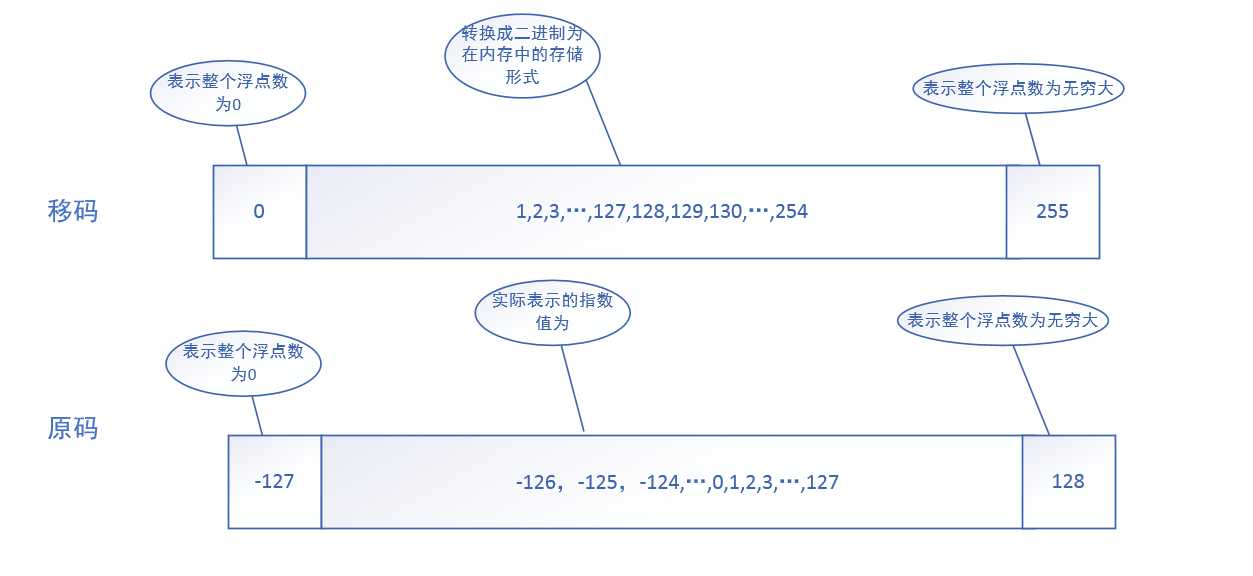
指数部分：

指数位用8位移码表示。8bit可表示256个数，用移码可表示的十进制范围为-127~128，将指数位的移码为0表示浮点数的指数为负无穷，整个浮点数为0；当指数的移码为255时表示指数为正无穷，浮点数为最大值。所以实际用来表示的移码范围为 1 ~ 254 ，转换成十进制原码为 -126 ~ 127，也就是整个指数部分（注意：只算指数部分）所能表示的最小的正数值为 $2^{-126}$ ，最大的值为 $2^{127}$ 。如图所示：

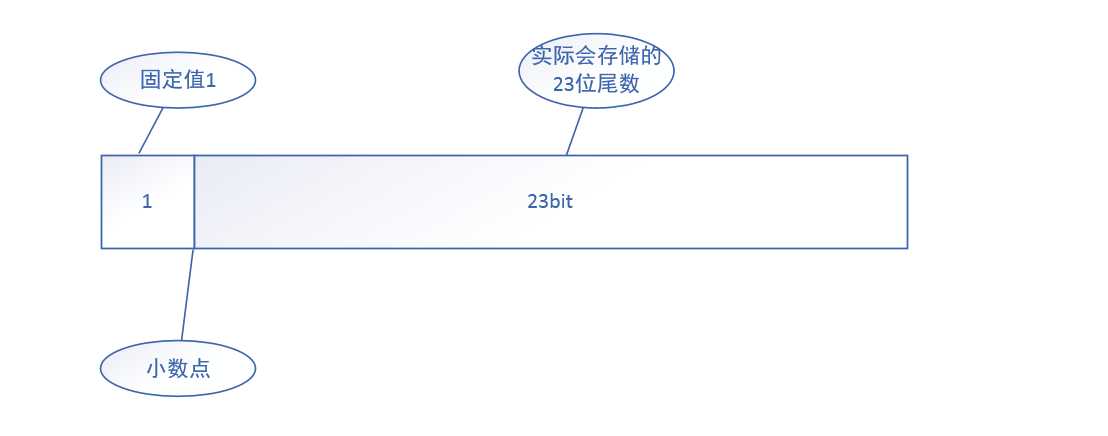
尾数部分：

尾数部分部分共23位，表示范围为0 ~ $2^{23}-1$ 。在规约式浮点数的尾数部分中小数点前还隐藏着一个固定的整数值整数1，尾数部分的23位只用来表示小数点后的值，这种方式可保证浮点数有唯一的表示形式。规约式浮点数尾数部分如图所示:

最小绝对值分析

对于规约式浮点数可表示的最小的正数为 $2^{-126}$ ,我们可用代码来验证：

    public static void main(final String[] args) throws InterruptedException
    { 
   
		
        BigDecimal b1 = new BigDecimal("0.5");
        System.out.println(b1.pow(126).floatValue()); //2的-126次方的浮点数值
        System.out.println(Float.MIN_NORMAL);//浮点数的最小规格化正数
    }

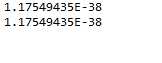
输出结果表明float的最小规约化正数为 $2^{-126}$ ：

当正数值小于 $2^{-126}$ 时，指数部分将变成-127，根据前面的指数部分的介绍，此时的浮点数应为0，我们使用代码来验证发现并不是0：


    public static void main(final String[] args) throws InterruptedException
    { 
   
        BigDecimal b1 = new BigDecimal("0.5");
        System.out.println(b1.pow(126).floatValue());
        System.out.println(b1.pow(127).floatValue());
    }

运行截图：

这是因为float类型采用了渐进式下溢出，当float类型的数小于 $2^{-126}$ 次方时将不继续采用规约式表示，而改为非规约式表示，所谓非规约式表示也就是摆脱了小数点前必须为1的限制，对于小于 $2^{-126}$ 的数小数点前可以为0。采用渐进式下溢出的原因是，如果不采用0与绝对值最小的浮点数之间距离将大于两个相邻浮点数之间的距离，且前者是后者的 $2^{23}$ 倍！！！（绝对值最小的规约式浮点数之前计算出为 $2^{-126}$ ,与0的距离为 $2^{-126}$ ,倒数第二小的值为 $(1+2^{-23}) \times 2^{-126}=2^{-126}+2^{-149}$ ,与 $2^{-126}$ 的距离为 $2^{-149}$ ）

当采用了渐进式下溢出，float类型所能表示的绝对值最小的数便为： $2^{-149}$ ,可用代码验证：


    public static void main(final String[] args) throws InterruptedException
    { 
   
        BigDecimal b1 = new BigDecimal("0.5");
        System.out.println(b1.pow(149).floatValue());
        System.out.println(Float.MIN_VALUE);
    }

运行结果为：

当浮点数的绝对值小于 $2^{-149}$ 时，则彻底超出了float所表示的最小绝对值，将会被表示成0。我们来验证一下 $2^{-150}$

    public static void main(final String[] args) throws InterruptedException
    { 
   
        BigDecimal b1 = new BigDecimal("0.5");
        System.out.println(b1.pow(150).floatValue());
    }

运行结果为：

综上所述，float类型的最小绝对值数为： $2^{-149}$

最大绝对值分析

最大绝对值就比较简单了，当尾数全为1，指数为127时为最大，也就是 $(2-2^{-23}) \times 2^{127}$
使用代码来验证下：


    public static void main(final String[] args) throws InterruptedException
    { 
   
        BigDecimal b1 = new BigDecimal("2");
        System.out.println(b1.pow(128).subtract(b1.pow(104)).floatValue());
        System.out.println(Float.MAX_VALUE);
    }

运行结果如下：

当大于 $(2-2^{-23}) \times 2^{127}$ 时，将显示无穷大：

    public static void main(final String[] args) throws InterruptedException
    { 
   
        BigDecimal b1 = new BigDecimal("2");
        System.out.println(b1.pow(128).add(new BigDecimal(1)).floatValue());

    }