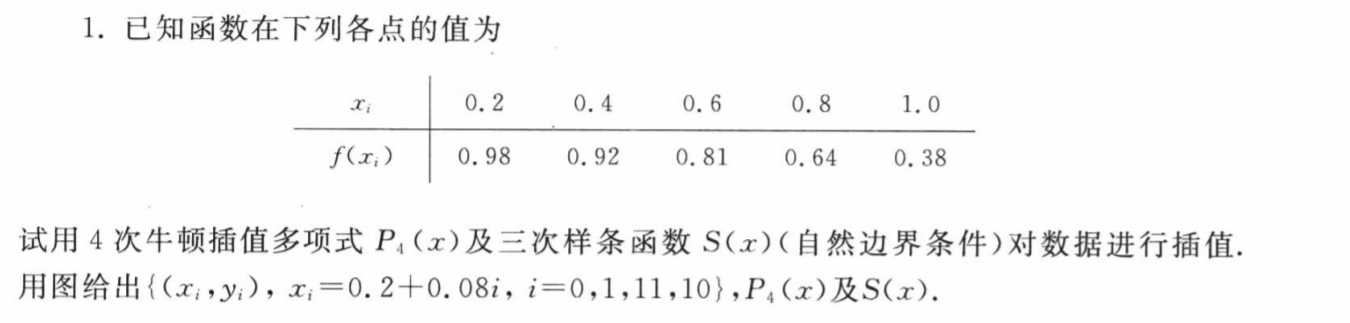
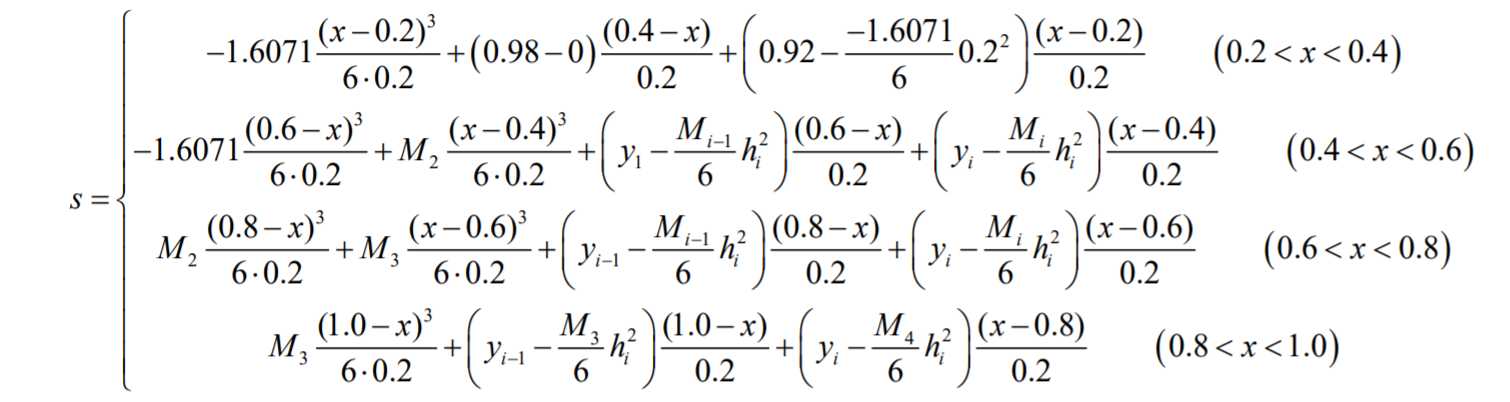目录
前言
必看 回顾前篇例题中的另一问题使用三次样条插值函数来求解插值点的函数值,那么本篇文章将继续承接上篇内容,主要讲述三次样条插值函数的原理及如何利用matlab来实现编程。如果没有看过前一篇的读者可以点击此链接: 数值分析(一) 牛顿插值法及matlab代码 回顾一下
一、三次样条插值
1. 三次样条函数定义
定义:函数定义在区间 [ a , b ] \left[a,b\right] [a,b]上,给定n+1个节点和一组与之对应的函数值,且函数满足:
1. 每个节点上满足 S ( x i ) = f ( x i ) ( i = 0 , 1 , ⋯ , n − 1 ) S\left(x_i\right)=f\left(x_i\right)\;\;\;\;\left(i=0,1,\cdots,n-1\right) S(xi)=f(xi)(i=0,1,⋯,n−1)
2. 在 [ a , b ] \left[a,b\right] [a,b]上有连续的二阶导数
3. 在每个小区间 [ x i , x i + 1 ] ( i = 0 , 1 , ⋯ , n − 1 ) \left[x_i,x_{i+1}\right]\left(i=0,1,\cdots,n-1\right) [xi,xi+1](i=0,1,⋯,n−1)上是一个三次多项式
则称 S ( x i ) S\left(x_i\right) S(xi)为 三次样条插值函数
2. 三次样条插值多项式
三次样条插值函数 S ( x ) S\left(x\right) S(x)是一个分段三次多项式,要求出 S ( x ) S\left(x\right) S(x),在每个小区间 [ x i , x i + 1 ] \left[x_i,x_{i+1}\right] [xi,xi+1]上要确定4个待定参数,若用 S i ( x ) S_i\left(x\right) Si(x)表示它在第i个子区间 [ x i , x i + 1 ] \left[x_i,x_{i+1}\right] [xi,xi+1]上的表达式,则 S i ( x ) = a i 0 + a i 1 x + a i 2 x 2 + a i 3 x 3 ( i = 0 , 1 , ⋯ , n − 1 ) S_i\left(x\right)=a_{i0}\;+a_{i1}x+a_{i2}x^2\;+a_{i3}x^3\;\;\;\left(i=0,1,\cdots,n-1\right) Si(x)=ai0+ai1x+ai2x2+ai3x3(i=0,1,⋯,n−1)注意 三次多项式 S ( x ) S\left(x\right) S(x)及其一阶导数 S ′ ( x ) S’\left(x\right) S′(x)和二阶导 S ′ ′ ( x ) S”\left(x\right) S′′(x)在整个插值区间上连续,在上述条件中再加入边界条件,即可求出各系数,常用的边界条件有三种类型。
3. 三次样条插值求法
在子区间 [ x i , x i + 1 ] \left[x_i,x_{i+1}\right] [xi,xi+1]上 S ( x ) = S i ( x ) S\left(x\right)=S_i\left(x\right) S(x)=Si(x)是三次多项式,所以 在此小区间上 S ′ ′ ( x ) S”\left(x\right) S′′(x)是x的线性函数,且因为 S ′ ′ ( x i − 1 ) = M i − 1 , S ′ ′ ( x i ) = M i x ∈ [ x i − 1 , x i ] S”\left(x_{i-1}\right)=M_{i-1},S”\left(x_i\right)=M_i\;\;\;\;x\in\left[x_{i-1},x_i\right] S′′(xi−1)=Mi−1,S′′(xi)=Mix∈[xi−1,xi],用线性插值,可知其表达式为 S i ′ ′ ( x ) = M i − 1 x − x i x i − 1 − x i + M i x − x i − 1 x i − x i − 1 S_i”\left(x\right)=M_{i-1}\frac{x-x_i}{x_{i-1}-x_i}+M_i\frac{x-x_{i-1}}{x_i-x_{i-1}} Si′′(x)=Mi−1xi−1−xix−xi+Mixi−xi−1x−xi−1 记 h i = x i − x i − 1 h_i=x_i-x_{i-1} hi=xi−xi−1,根据上式则可得到 S i ′ ′ ( x ) = M i − 1 x i − x h i + M i x − x i − 1 h i S_i”\left(x\right)=M_{i-1}\frac{x_i-x}{h_i}+M_i\frac{x-x_{i-1}}{h_i} Si′′(x)=Mi−1hixi−x+Mihix−xi−1 通过两次连续积分可得到: S i = M i − 1 ( x i − x ) 3 6 h i + M i ( x − x i − 1 ) 3 6 h i + A i ( x i − x ) + B i ( x − x i − 1 ) S_i=M_{i-1}\frac{\left(x_i-x\right)^3}{6h_i}+M_i\frac{\left(x-x_{i-1}\right)^3}{6h_i}+A_i\left(x_i-x\right)+B_i\left(x-x_{i-1}\right) Si=Mi−16hi(xi−x)3+Mi6hi(x−xi−1)3+Ai(xi−x)+Bi(x−xi−1) 其中 A i A_i Ai, B i B_i Bi是积分常数根据插值条件 S ( x i − 1 ) = f ( x i − 1 ) , S ( x i ) = f ( x i ) S\left(x_{i-1}\right)=f\left(x_{i-1}\right),S\left(x_i\right)=f\left(x_i\right) S(xi−1)=f(xi−1),S(xi)=f(xi)确定,即 A i A_i Ai, B i B_i Bi满足: S ( x i − 1 ) = 1 6 M i − 1 h i 2 + A i h i = f ( x i − 1 ) , S ( x i ) = 1 6 M i h i 2 + B i h i = f ( x i ) S\left(x_{i-1}\right)=\frac16M_{i-1}h_i^2+A_ih_i=f\left(x_{i-1}\right),S\left(x_i\right)=\frac16M_ih_i^2+B_ih_i=f\left(x_i\right) S(xi−1)=61Mi−1hi2+Aihi=f(xi−1),S(xi)=61Mihi2+Bihi=f(xi) 并记 f ( x i − 1 ) = y i − 1 , f ( x i ) = y i f\left(x_{i-1}\right)=y_{i-1},f\left(x_i\right)=y_i f(xi−1)=yi−1,f(xi)=yi,则得到 A i = 1 h i ( y i − 1 − 1 6 M i − 1 h i 2 ) , B i = 1 h i ( y i − 1 6 M i h i 2 ) A_i=\frac1{h_i}\left(y_{i-1}-\frac16M_{i-1}h_i^2\right),B_i=\frac1{h_i}\left(y_i-\frac16M_ih_i^2\right) Ai=hi1(yi−1−61Mi−1hi2),Bi=hi1(yi−61Mihi2) 将求得的 A i A_i Ai, B i B_i Bi代入式子中 S i = M i − 1 ( x i − x ) 3 6 h i + M i ( x − x i − 1 ) 3 6 h i + 1 h i ( y i − 1 − 1 6 M i − 1 h i 2 ) ( x i − x ) + 1 h i ( y i − 1 6 M i h i 2 ) ( x − x i − 1 ) ( x ∈ [ x i − 1 , x i ] , i = 1 , 2 , ⋯ , n ) S_i=M_{i-1}\frac{\left(x_i-x\right)^3}{6h_i}+M_i\frac{\left(x-x_{i-1}\right)^3}{6h_i}+\frac1{h_i}\left(y_{i-1}-\frac16M_{i-1}h_i^2\right)\left(x_i-x\right)+\frac1{h_i}\left(y_i-\frac16M_ih_i^2\right)\left(x-x_{i-1}\right)\\\left(x\in\left[x_{i-1},x_i\right],i=1,2,\cdots,n\right) Si=Mi−16hi(xi−x)3+Mi6hi(x−xi−1)3+hi1(yi−1−61Mi−1hi2)(xi−x)+hi1(yi−61Mihi2)(x−xi−1)(x∈[xi−1,xi],i=1,2,⋯,n) 由上讨论可知,只要确定 M 0 , M 1 , … , M n M_0,M_1,\dots,M_n M0,M1,…,Mn 这n+1个值, 就可定出三样条插值函数S(x)。
为了求出 M i ( i = 0 , 1 , ⋯ , n ) M_i\left(i=0,1,\cdots,n\right) Mi(i=0,1,⋯,n),利用一阶导数在子区间 [ x i , x i + 1 ] \left[x_i,x_{i+1}\right] [xi,xi+1]连接点上连续的条件 S ′ ( x i − 0 ) = S ′ ( x i + 0 ) S’\left(x_i-0\right)=S’\left(x_i+0\right) S′(xi−0)=S′(xi+0),通过一系列变换
求得 h i h i + h i + 1 M i − 1 + 2 M i + h i + 1 h i + h i + 1 M i + 1 = 6 h i + h i + 1 ( y i + 1 − y i h i + 1 − y i − y i − 1 h i ) \frac{h_i}{h_i+h_{i+1}}M_{i-1}+2M_i+\frac{h_{i+1}}{h_i+h_{i+1}}M_{i+1}=\frac6{h_i+h_{i+1}}\left(\frac{y_{i+1}-y_i}{h_{i+1}}-\frac{y_i-y_{i-1}}{h_{i}}\right) hi+hi+1hiMi−1+2Mi+hi+hi+1hi+1Mi+1=hi+hi+16(hi+1yi+1−yi−hiyi−yi−1)
(注意:由于过程有点小繁琐,本博主就偷个懒,直接把求好的公式展示出来。如果有读者非常想要了解详细计算步骤,读者可以参考教材《数值分析第5版__李庆扬,王能超,易大义编_北京:清华大学出版社》,在书的P42-43页 可以找到过程)
若记: { μ i = h i h i + h i + 1 λ i = h i + 1 h i + h i + 1 = 1 − μ i g i = 6 h i + h i + 1 ( y i + 1 − y i h i + 1 − y i − y i − 1 h i + 1 ) = 6 h i + h i + 1 ( f [ x i , x i + 1 ] − f [ x i − 1 , x i ] ) \left\{\begin{array}{l}\mu_i=\frac{h_i}{h_i+h_{i+1}}\\\\\lambda_i=\frac{h_{i+1}}{h_i+h_{i+1}}=1-\mu_i\\\\g_i=\frac6{h_i+h_{i+1}}\left(\frac{y_{i+1}-y_i}{h_{i+1}}-\frac{y_i-y_{i-1}}{h_{i+1}}\right)=\frac6{h_i+h_{i+1}}\left(f\left[x_i,x_{i+1}\right]-f\left[x_{i-1},x_i\right]\right)\end{array}\right. ⎩
⎨
⎧μi=hi+hi+1hiλi=hi+hi+1hi+1=1−μigi=hi+hi+16(hi+1yi+1−yi−hi+1yi−yi−1)=hi+hi+16(f[xi,xi+1]−f[xi−1,xi])
则简写方程 μ i M i − 1 + 2 M i + λ i M i + 1 = g i ( i = 1 , 2 , ⋯ , n − 1 ) \mu_iM_{i-1}+2M_i+\lambda_iM_{i+1}=g_i\;\;\;\;\;\;\;\;\left(i=1,2,\cdots,n-1\right) μiMi−1+2Mi+λiMi+1=gi(i=1,2,⋯,n−1)
即: { μ 1 M 0 + 2 M 1 + λ 1 M 2 = g 1 μ 2 M 1 + 2 M 2 + λ 2 M 3 = g 2 ⋯ μ n − 1 M n − 2 + 2 M n − 1 + λ n − 1 M n = g n − 1 \left\{\begin{array}{l}\mu_1M_0+2M_1+\lambda_1M_2=g_1\\\mu_2M1+2M_2+\lambda_2M_3=g_2\\\cdots\\\mu_{n-1}M_{n-2}+2M_{n-1}+\lambda_{n-1}M_n=g_{n-1}\end{array}\right. ⎩
⎨
⎧μ1M0+2M1+λ1M2=g1μ2M1+2M2+λ2M3=g2⋯μn−1Mn−2+2Mn−1+λn−1Mn=gn−1
3.1 第一种类型
给定两端点的一阶导数值: S ′ ( x 0 ) = f ′ ( x 0 ) = y 0 ′ , S ′ ( x n ) = f ′ ( x n ) = y n ′ S’\left(x_0\right)=f’\left(x_0\right)=y’_0,S’\left(x_n\right)=f’\left(x_n\right)=y’_n S′(x0)=f′(x0)=y0′,S′(xn)=f′(xn)=yn′
根据第一类型条件可得: 2 M 0 + M 1 = 6 h 1 ( y 1 − y 0 h 1 − y 0 ′ ) M n − 1 + 2 M n = 6 h n ( y n ′ − y n − y n − 1 h n ) 2M_0+M_1=\frac6{h_1}\left(\frac{y_1-y_0}{h_1}-y’_0\right)\\M_{n-1}+2M_n=\frac6{h_n}\left(y’_n-\frac{y_n-y_{n-1}}{h_n}\right) 2M0+M1=h16(h1y1−y0−y0′)Mn−1+2Mn=hn6(yn′−hnyn−yn−1) 根据之前式子整合后可以得到关于 M 0 , M 1 , ⋯ M n M_0,M_1,\cdots M_n M0,M1,⋯Mn线性方程方程如下: [ 2 1 μ 1 2 λ 1 ⋱ ⋱ ⋱ μ n − 1 2 λ n − 1 1 2 ] [ M 0 M 1 ⋮ M n − 1 M n ] = [ g 0 g 1 ⋮ g n − 1 g n ] \begin{bmatrix}2&1&&&\\\mu_1&2&\lambda_1&&\\&\ddots&\ddots&\ddots&\\&&\mu_{n-1}&2&\lambda_{n-1}\\&&&1&2\end{bmatrix}\begin{bmatrix}M_0\\M_1\\\vdots\\M_{n-1}\\M_n\end{bmatrix}=\begin{bmatrix}g_0\\g_1\\\vdots\\g_{n-1}\\g_n\end{bmatrix}
2μ112⋱λ1⋱μn−1⋱21λn−12
M0M1⋮Mn−1Mn
=
g0g1⋮gn−1gn
其中 { g 0 = 6 h 1 ( f [ x 0 , x 1 ] − y 0 ′ ) g n = 6 h n ( y n ′ − f [ x n − 1 , x n ] ) \left\{\begin{array}{l}g_0=\frac6{h_1}\left(f\left[x_0,x_1\right]-y’_0\right)\\\\g_n=\frac6{h_n}\left(y’_n-f\left[x_{n-1},x_n\right]\right)\end{array}\right. ⎩
⎨
⎧g0=h16(f[x0,x1]−y0′)gn=hn6(yn′−f[xn−1,xn])
3.2 第二种类型
给定两端点的二阶导数值: S ′ ′ ( x 0 ) = f ′ ′ ( x 0 ) = y 0 ′ ′ , S ′ ′ ( x n ) = f ′ ′ ( x n ) = y n ′ ′ S”\left(x_0\right)=f”\left(x_0\right)=y”_0,S”\left(x_n\right)=f”\left(x_n\right)=y”_n S′′(x0)=f′′(x0)=y0′′,S′′(xn)=f′′(xn)=yn′′
作为特例, S ′ ′ ( x 0 ) = S ′ ′ ( x n ) = 0 S”\left(x_0\right)=S”\left(x_n\right)=0 S′′(x0)=S′′(xn)=0称为 自然边界条件。满足自然边界条件的三次样条插值函数称为 自然样条插值函数。
其中令 M 0 = y 0 ′ ′ , M n = y n ′ ′ M_0=y”_0,M_n=y”_n M0=y0′′,Mn=yn′′ 从而得到第二种类型关于 M 1 , M 2 , ⋯ M n − 1 M_1,M_2,\cdots M_{n-1} M1,M2,⋯Mn−1线性方程方程 [ 2 λ 1 μ 2 2 λ 2 ⋱ ⋱ ⋱ μ n − 2 2 λ n − 2 μ n − 1 2 ] [ M 1 M 2 ⋮ M n − 2 M n − 1 ] = [ g 1 − μ 1 y 0 ′ ′ g 2 ⋮ g n − 2 g n − 1 − λ n − 1 y n ′ ′ ] \begin{bmatrix}2&\lambda_1&&&\\\mu_2&2&\lambda_2&&\\&\ddots&\ddots&\ddots&\\&&\mu_{n-2}&2&\lambda_{n-2}\\&&&\mu_{n-1}&2\end{bmatrix}\begin{bmatrix}M_1\\M_2\\\vdots\\M_{n-2}\\M_{n-1}\end{bmatrix}=\begin{bmatrix}g_1-\mu_1y”_0\\g_2\\\vdots\\g_{n-2}\\g_{n-1}-\lambda_{n-1}y”_n\end{bmatrix}
2μ2λ12⋱λ2⋱μn−2⋱2μn−1λn−22
M1M2⋮Mn−2Mn−1
=
g1−μ1y0′′g2⋮gn−2gn−1−λn−1yn′′
3.3 第三种类型
当 f ( x ) f\left(x\right) f(x)是以为 x n − x 0 x_n-x_0 xn−x0周期的函数时,则要求 S ( x ) S\left(x\right) S(x)也是周期函数,这时边界条件应满足当 f ( x 0 ) = f ( x n ) f\left(x_0\right)=f\left(x_n\right) f(x0)=f(xn)时, S ′ ( x 0 + 0 ) = S ′ ( x n − 0 ) , S ′ ′ ( x 0 + 0 ) = S ′ ′ ( x n − 0 ) S’\left(x_0+0\right)=S’\left(x_n-0\right),S”\left(x_0+0\right)=S”\left(x_n-0\right) S′(x0+0)=S′(xn−0),S′′(x0+0)=S′′(xn−0) 由上述条件可以得到: M 0 = M n , λ n M 1 + μ n M n − 1 + 2 M n = g n M_0=M_n,\lambda_nM_1+\mu_nM_{n-1}+2M_n=g_n M0=Mn,λnM1+μnMn−1+2Mn=gn
其中: { μ n = h n h 1 + h n + 1 λ i = h n h 1 + h n = 1 − μ i g i = 6 h 1 + h n ( f [ x 0 , x 1 ] − f [ x n − 1 , x n ] ) \left\{\begin{array}{l}\mu_n=\frac{h_n}{h_1+h_{n+1}}\\\\\lambda_i=\frac{h_n}{h_1+h_n}=1-\mu_i\\\\g_i=\frac6{h_1+h_n}\left(f\left[x_0,x_1\right]-f\left[x_{n-1},x_n\right]\right)\end{array}\right. ⎩
⎨
⎧μn=h1+hn+1hnλi=h1+hnhn=1−μigi=h1+hn6(f[x0,x1]−f[xn−1,xn]) 关于 M 1 , M 2 , ⋯ M n M_1,M_2,\cdots M_n M1,M2,⋯Mn线性方程 [ 2 λ 1 μ 1 μ 2 2 λ 2 ⋱ ⋱ ⋱ μ n − 1 2 λ n − 1 λ n μ n 2 ] [ M 1 M 2 ⋮ M n − 1 M n ] = [ g 1 g 2 ⋮ g n − 1 g n ] \begin{bmatrix}2&\lambda_1&&&\mu_1\\\mu_2&2&\lambda_2&&\\&\ddots&\ddots&\ddots&\\&&\mu_{n-1}&2&\lambda_{n-1}\\\lambda_n&&&\mu_n&2\end{bmatrix}\begin{bmatrix}M_1\\M_2\\\vdots\\M_{n-1}\\M_n\end{bmatrix}=\begin{bmatrix}g_1\\g_2\\\vdots\\g_{n-1}\\g_n\end{bmatrix}
2μ2λnλ12⋱λ2⋱μn−1⋱2μnμ1λn−12
M1M2⋮Mn−1Mn
=
g1g2⋮gn−1gn
读者注意:上述三种边界条件所求的三次样条插值函数各有所不同,虽然式子都长得差不多还是有很多细微的差别,请读者认真仔细阅读。
二、三次样条插值公式matlab程序
本文章主要是衔接上篇文章的第二小问进行编写,在此先讲三次样条插值公式(第二类型),如有没看过前一章的读者可以点击此链接 数值分析(一) 牛顿插值法及matlab代码 回顾一下。
1. 三次样条插值公式(第二种类型)
下面展示三次样条插值公式(第二种类型)代码
function [D,h,A,g,M]=threesimple(X,Y)
% 自然边界条件的三次样条函数(第二种边界条件)
% 此函数为M值求值函数
% D,h,A,g,M输出量分别为系数矩阵D,插值宽度h,差商表A,g值,M值
n=length(X);
A=zeros(n,n);A(:,1)=Y';D=zeros(n-2,n-2);g=zeros(n-2,1);
for j=2:n
for i=j:n
A(i,j)=(A(i,j-1)- A(i-1,j-1))/(X(i)-X(i-j+1));
end
end
for i=1:n-1
h(i)=X(i+1)-X(i);
end
for i=1:n-2
D(i,i)=2;
g(i,1)=(6/(h(i+1)+h(i)))*(A(i+2,2)-A(i+1,2));
end
for i=2:n-2
u(i)=h(i)/(h(i)+h(i+1));
n(i-1)=h(i)/(h(i-1)+h(i));
D(i-1,i)=n(i-1);
D(i,i-1)=u(i);
end
M=D\g;
M=[0;M;0];
end
function s=threesimple1(X,Y,x)
% 自然边界条件函数
% s函数表示三次样条插值函数插值点对应的函数值
% 根据三次样条参数函数求出的D,h,A,g,M
% x表示求解插值点函数点,X为已知插值点
[D,h,A,g,M]=threesimple(X,Y)
n=length(X); m=length(x);
for t=1:m
for i=1:n-1
if (x(t)<=X(i+1))&&(x(t)>=X(i))
p1=M(i,1)*(X(i+1)-x(t))^3/(6*h(i));
p2=M(i+1,1)*(x(t)-X(i))^3/(6*h(i));
p3=(A(i,1)-M(i,1)/6*(h(i))^2)*(X(i+1)-x(t))/h(i);
p4=(A(i+1,1)-M(i+1,1)/6*(h(i))^2)*(x(t)-X(i))/h(i);
s(t)=p1+p2+p3+p4;
break;
else
s(t)=0;
end
end
end
end
2 例题
衔接上篇文章实例中提到的所有问题,在此篇文章中全部解决,问题如下:
上篇文章已经处理了牛顿插值问题,那么接下来处理三次样条插值问题
利用前文所给出的三次样条(自然边界条件)的函数代码,在命令框中输入如下语句:
clear all
format short
x=0.2:0.2:1;
y=[0.98 0.92 0.81 0.64 0.38];
x0=[0.2 0.28 1.0 1.08];
s=threesimple1(x,y,x0)
运行后结果如下所示,在这里显示很多数据其中D,h,A,g,M输出量分别为系数矩阵D,插值宽度h,差商表A,g值,M值
结果分析: 根据计算结果可以看到最后一个点x=1.08时输出值为0,由于原先给定的区间是[0,1]之间,而1.08是不在区间范围内的,所以在编写程序时,有个判断若超出区域边界值,直接将其函数值赋值0。
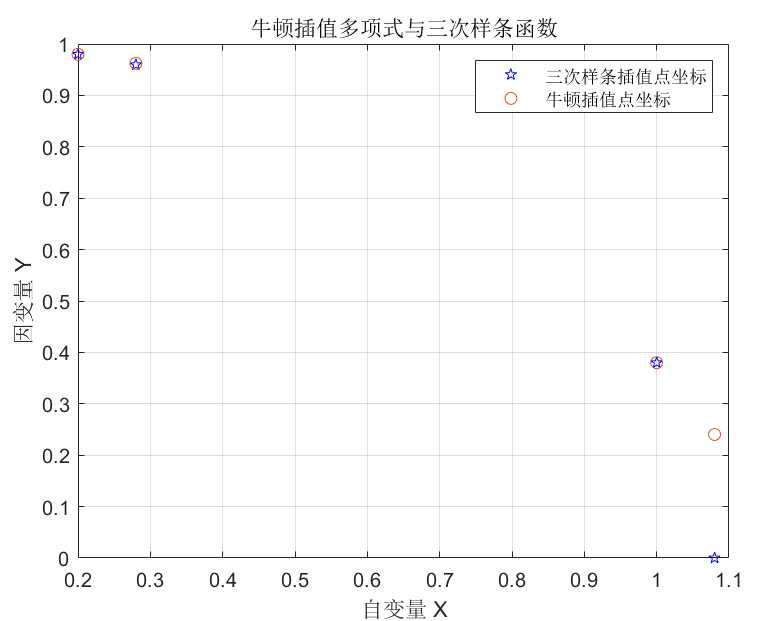
题中还提及到将点画在坐标上,在命令行中输入代码段
plot(x0,s,'bp')
hold on
grid
plot(x0,y,'o')
xlabel('自变量 X'), ylabel('因变量 Y')
title('牛顿插值多项式与三次样条函数')
legend('三次样条插值点坐标','牛顿插值点坐标')
显示的图如下所示:
最后S(x)函数如下:(注意文章写的有点晚了就偷个懒,里面的M值有些没写,不过之前求的M值都有只需要往里填就行)
根据有些读者建议,完善一下本文再将函数图像绘制出来代码如下:
clear all
format short
x=0.2:0.2:1;
y=[0.98 0.92 0.81 0.64 0.38];
x0=0.1:0.001:1.1;
s=threesimple1(x,y,x0)
plot(x0,s)
hold on
grid on
plot(x,y,'o')
xlabel('自变量 X'), ylabel('因变量 Y')
title('插值点与三次样条函数')
legend('三次样条插值点坐标','插值点')
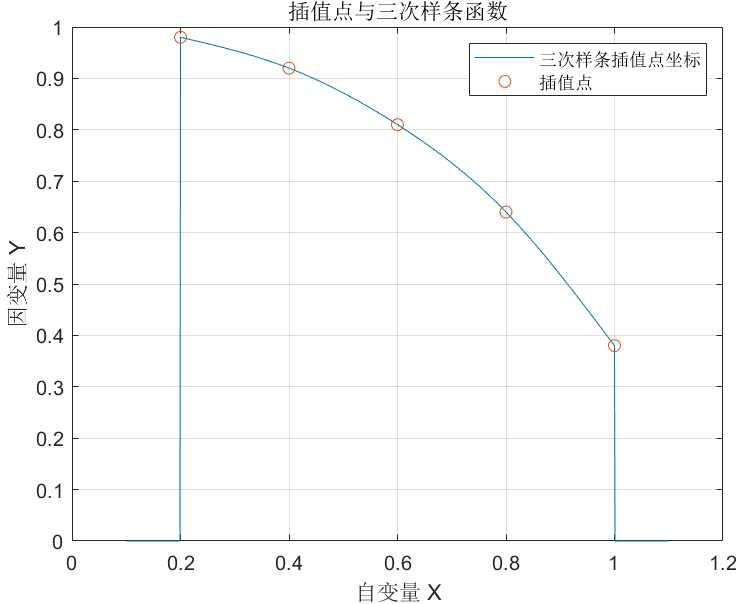
运行后的结果如下:
三、 总结
整合上一篇牛顿插值法,再结合本篇文章三次样条插值法,将这道计算实习题完整做完了。这里我也只提供第二种边界条件的最特殊的条件函数,之后我看有时间再做一篇关于三种类型的完整函数。我之后上传这个 实习计算题的完整代码 ,以供读者参考,也希望读者有能力可以提升我写的函数。感谢读者耐心的观看,希望读者读完后可以学到很多。
四、 补充
感谢大家的观看,有很多问了我许多问题,问我最多问题:每段表达式系数输与表达式怎么输出,针对大家的这些疑问我将更新的代码放到下一篇文章中,文章的连接如下(2022.5.3):
五、插值法专栏
专栏链接:插值法专栏,如果对你有帮助的话可以点个赞,点个订阅,我将完善此专栏
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/35925.html