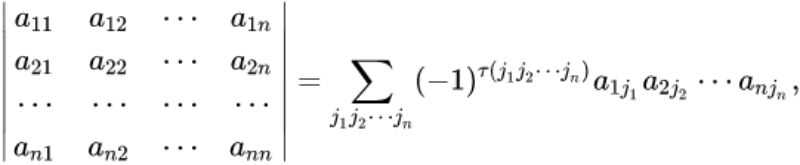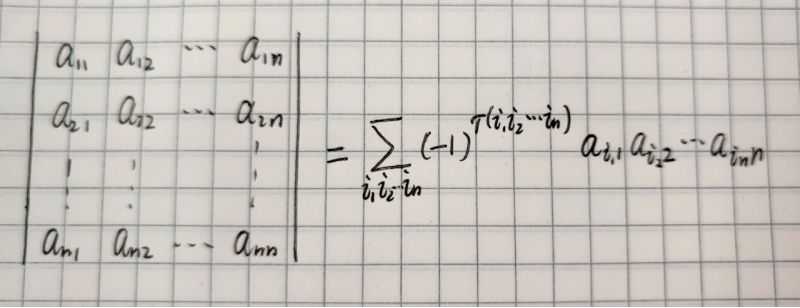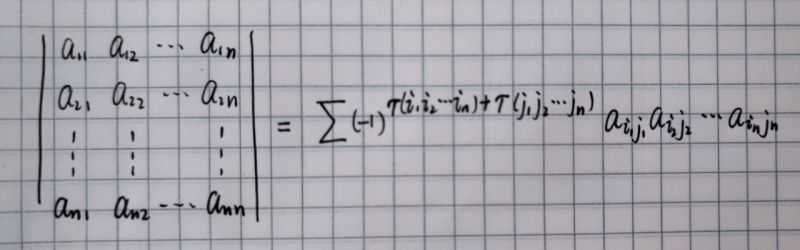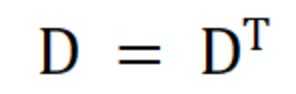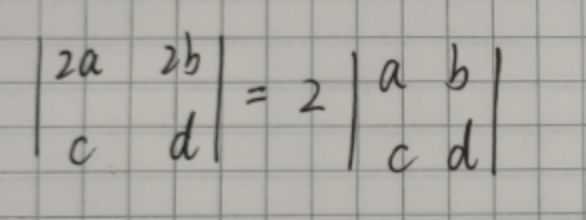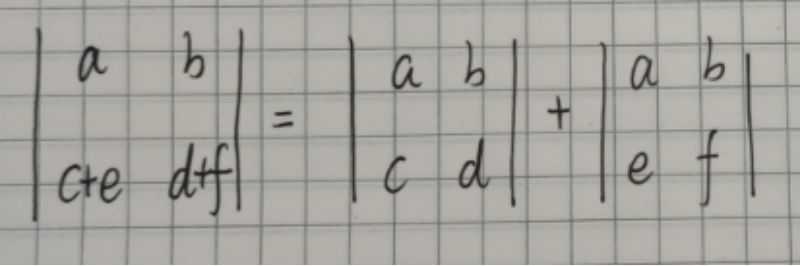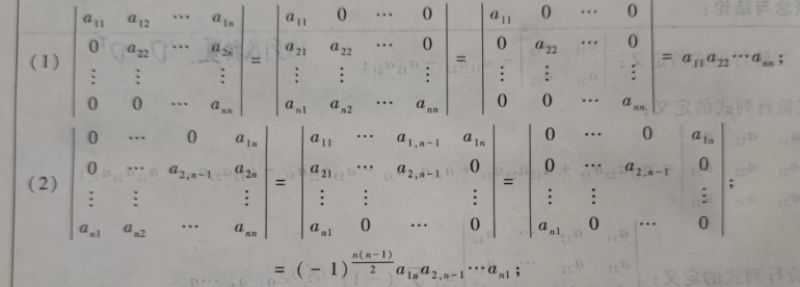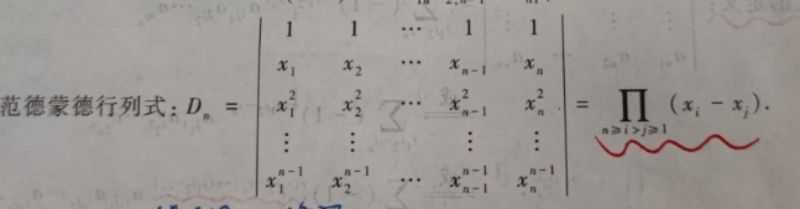目录
基础定义
● 1.n级排列:由自然数1,2,…,n 组成的一个有序数组。
推论:在n级排列中,奇排列与偶排列各占 n!/2
● 2.逆序:大数排在小数的前面
● 3.逆序数:一个排列中逆序的总数
● 4.排列
偶排列:逆序数为偶数
奇排列:逆序数为奇数
标准排列:自然数1,2,…,n按由小到大的排列
n阶行列式的定义
1.按行展开
● 行标取标准排列,列标取所有排列的可能
● 其中该式代表列标的逆序数
2.按列展开
● 列标取标准排列,行标取所有排列的可能
3.随意展开
● 行标和列标都任意取尽排列的所有可能
行列式性质
1.转置行列式,值不变
行列式转置:将每一行和每一列互换
2.互换行列式的两行(列),行列式符号改变
3.行列式某一行(列)的公因子可以提到行列式外
4.行列式的某一行(列)的元素都是两个数的和,则该行列式等于两个行列式的和
5.将行列式某一行(列)的k倍加到另一行(列)对应元素上,行列式值不变
性质推论
● 1.两行相等或对应成比例,D = 0
● 2.某一行(列)全为0,D = 0
行列式展开定理
● 余子式:去掉某个元素所在的行列后,剩余的n-1阶行列式
● 代数余子式:余子式*(-1)^(行标+列标)
● 行列式展开公式
降阶
选0多的行或列展开
异乘变零定理:某行(列)元素与另一行(列)元素的代数余子式乘积之和为0
拉普拉斯定理:
在n阶行列式D=|aij| 中,任意取定k行(列),1≤k≤n-1,由这k行(列)的元素所构成的一切k阶子式与其代数余子式的乘积的和等于行列式D的值。
● 拉普拉斯定理展开计算量较大,可在某k行0较多的情况下使用,快速降阶
公式与法则
上(下)三角行列式
范德蒙德行列式
克拉默法则
计算量较大,一般不用
两个推论
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/37634.html