简介
混淆矩阵是ROC曲线绘制的基础,同时它也是衡量分类型模型准确度中最基本,最直观,计算最简单的方法。
一句话解释版本:
混淆矩阵就是分别统计分类模型归错类,归对类的观测值个数,然后把结果放在一个表里展示出来。这个表就是混淆矩阵。
数据分析与挖掘体系位置
混淆矩阵是评判模型结果的指标,属于模型评估的一部分。此外,混淆矩阵多用于判断分类器(Classifier)的优劣,适用于分类型的数据模型,如分类树(Classification Tree)、逻辑回归(Logistic Regression)、线性判别分析(Linear Discriminant Analysis)等方法。
在分类型模型评判的指标中,常见的方法有如下三种:
- 混淆矩阵(也称误差矩阵,Confusion Matrix)
- ROC曲线
- AUC面积
本篇主要介绍第一种方法,即混淆矩阵,也称误差矩阵。
此方法在整个数据分析与挖掘体系中的位置如下图所示。
混淆矩阵的定义
混淆矩阵(Confusion Matrix),它的本质远没有它的名字听上去那么拉风。矩阵,可以理解为就是一张表格,混淆矩阵其实就是一张表格而已。
以分类模型中最简单的二分类为例,对于这种问题,我们的模型最终需要判断样本的结果是0还是1,或者说是positive还是negative。
我们通过样本的采集,能够直接知道真实情况下,哪些数据结果是positive,哪些结果是negative。同时,我们通过用样本数据跑出分类型模型的结果,也可以知道模型认为这些数据哪些是positive,哪些是negative。
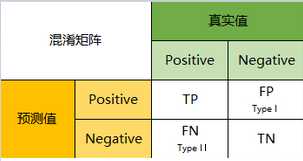
因此,我们就能得到这样四个基础指标,我称他们是一级指标(最底层的):
- 真实值是positive,模型认为是positive的数量(True Positive=TP)
- 真实值是positive,模型认为是negative的数量(False Negative=FN):这就是统计学上的第二类错误(Type II Error)
- 真实值是negative,模型认为是positive的数量(False Positive=FP):这就是统计学上的第一类错误(Type I Error)
- 真实值是negative,模型认为是negative的数量(True Negative=TN)
将这四个指标一起呈现在表格中,就能得到如下这样一个矩阵,我们称它为混淆矩阵(Confusion Matrix):
混淆矩阵的指标
预测性分类模型,肯定是希望越准越好。那么,对应到混淆矩阵中,那肯定是希望TP与TN的数量大,而FP与FN的数量小。所以当我们得到了模型的混淆矩阵后,就需要去看有多少观测值在第二、四象限对应的位置,这里的数值越多越好;反之,在第一、三象限对应位置出现的观测值肯定是越少越好。
二级指标
但是,混淆矩阵里面统计的是个数,有时候面对大量的数据,光凭算个数,很难衡量模型的优劣。因此混淆矩阵在基本的统计结果上又延伸了如下4个指标,我称他们是二级指标(通过最底层指标加减乘除得到的):
- 准确率(Accuracy)—— 针对整个模型
- 精确率(Precision)
- 灵敏度(Sensitivity):就是召回率(Recall)
- 特异度(Specificity)
我用表格的方式将这四种指标的定义、计算、理解进行了汇总:
通过上面的四个二级指标,可以将混淆矩阵中数量的结果转化为0-1之间的比率。便于进行标准化的衡量。
在这四个指标的基础上在进行拓展,会产令另外一个三级指标
三级指标
这个指标叫做F1 Score。他的计算公式是:
其中,P代表Precision,R代表Recall。
F1-Score指标综合了Precision与Recall的产出的结果。F1-Score的取值范围从0到1的,1代表模型的输出最好,0代表模型的输出结果最差。
混淆矩阵的实例
当分类问题是二分问题是,混淆矩阵可以用上面的方法计算。当分类的结果多于两种的时候,混淆矩阵同时适用。
一下面的混淆矩阵为例,我们的模型目的是为了预测样本是什么动物,这是我们的结果:
通过混淆矩阵,我们可以得到如下结论:
Accuracy
在总共66个动物中,我们一共预测对了10 + 15 + 20=45个样本,所以准确率(Accuracy)=45/66 = 68.2%。
以猫为例,我们可以将上面的图合并为二分问题:
Precision
所以,以猫为例,模型的结果告诉我们,66只动物里有13只是猫,但是其实这13只猫只有10只预测对了。模型认为是猫的13只动物里,有1条狗,两只猪。所以,Precision(猫)= 10/13 = 76.9%
Recall
以猫为例,在总共18只真猫中,我们的模型认为里面只有10只是猫,剩下的3只是狗,5只都是猪。这5只八成是橘猫,能理解。所以,Recall(猫)= 10/18 = 55.6%
Specificity
以猫为例,在总共48只不是猫的动物中,模型认为有45只不是猫。所以,Specificity(猫)= 45/48 = 93.8%。
虽然在45只动物里,模型依然认为错判了6只狗与4只猫,但是从猫的角度而言,模型的判断是没有错的。
(这里是参见了Wikipedia,Confusion Matrix的解释,https://en.wikipedia.org/wiki/Confusion_matrix)
F1-Score
通过公式,可以计算出,对猫而言,F1-Score=(2 * 0.769 * 0.556)/( 0.769 + 0.556) = 64.54%
同样,我们也可以分别计算猪与狗各自的二级指标与三级指标值。
ROC曲线在R中的实现
library(ISLR)
cor(Smarket[,-9])
attach(Smarket)
# logistic Model
model_LR <- glm(Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 + Volume,
family = binomial,
data = Smarket)
# Make prediction
prob_LR <- predict(model_LR, type = 'response', newdata = Smarket[1:300,])
prob_LR <- predict(model_LR, type = 'response', newdata = Smarket[,])
# create a vector of class predictions based on wether the predicted probability of a market increase is greater than or less than 0.5
pred_LR <- rep("Down" , 1250)
pred_LR[prob_LR > 0.5] = 'Up'
# Confusion Matrix
table(pred_LR, Direction)
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/37971.html