微分方程回顾

微分方程是用来描述某一类函数与其导数之间的关系的方程，其解是一个符合方程的函数。（解为常数值的是代数方程）

微分方程的求解是研究微分方程的重点之一，例如解是否存在，存在是否唯一等等。只有少数类型的微分方程存在解析解；无法求得解析解时，可以求数值解（用程序做数值分析），以此确认其解的部分性质。

微分方程按自变量的个数可分为常微分方程（Ordinary Differential Equations）和偏微分方程（Partial Differential Equations），前者只有一个自变量，表达通式形如
$$f(\frac{d^{n}y}{d{x}^n},\frac{d^{(n-1)}y}{d{x}^{(n-1)}},...,\frac{dy}{dx},y)=p(x).$$
后者有两个及以上自变量，例如$$\frac{\partial \varphi }{\partial x}+x\frac{\partial \varphi }{\partial y}=0.$$

以常微分方程为例讲一下常见的一些概念，其中包括 （非）齐次，常（变）系数，（非）线性 。

如果第一个公式里左侧为线性微分方程（前提条件），且右侧的$p(x)=0$，则为齐次线性微分方程，否则非齐次。出现齐次概念的另一个场合是一阶微分方程$f(x,y)dy=g(x,y)dx$，具体可以参见Wikipedia 齐次微分方程。简单来说，如果方程的解是齐次函数，那么这个方程就是齐次方程。

常系数和变系数就看函数及其各阶导数前系数是否为常数。

线性，则取决于函数本身是否线性以及函数是否与其导数有乘积，跟自变量无关。
例如：

• 非齐次二级线性微分方程：$$\frac{d^{2}y}{d{x}^2}+x\frac{dy}{dx}+xy=x+1$$
• 谐振子齐次二阶常系数微分方程：
  $$\frac{d^{2}u}{d{x}^2}+{\omega }^{2}u=0$$
• 单摆二阶非线性微分方程：$$L\frac{d^{2}u}{d{x}^2}+gsin(u)=0$$
• 一阶非线性微分方程：$$\frac{dy}{dx}+y^2=x+1$$

微分方程：python 解析解（SymPy）

具备解析解的ODE，我们可以利用python的三方包SymPy进行求解。
以求解阻尼谐振子的二阶ODE为例，其表达式为
$$\begin{gathered} \frac{d^{2}x(t)}{d{t}^2}+2\gamma {\omega }_0\frac{dx(t)}{dt}+{\omega }_0^{2}x(t)=0, \\ initialconditions.\{\begin{array}{l}x(0)=0,\\ \frac{dx(t)}{dt}{|}_{t=0}=0.\end{array} \end{gathered}$$
完整的求解过程如下代码所示。

import numpy as np
from scipy import integrate
#import matplotlib.pyplot as plt
import sympy

def apply_ics(sol, ics, x, known_params):
	""" Apply the initial conditions (ics), given as a dictionary on the form ics = {y(0): y0, y(x).diff(x).subs(x, 0): yp0, ...}, to the solution of the ODE with independent variable x. The undetermined integration constants C1, C2, ... are extracted from the free symbols of the ODE solution, excluding symbols in the known_params list. """

	free_params = sol.free_symbols - set(known_params)
    ## free parameters like C1,C2, that needed to be figured out with ics and boundary conditions
	eqs = [(sol.lhs.diff(x, n) - sol.rhs.diff(x, n)).subs(x, 0).subs(ics) for n in range(len(ics))]
    ## form equations with general solution(sol), by substituting the x with 0 and [y(0),dy/dx(x=0)...] with ics.
	sol_params = sympy.solve(eqs, free_params)
    ## solve the algebraic equation set to get the free parameters expression
    ## return the solution after substituting the free parameters

	return sol.subs(sol_params)

sympy.init_printing()
## initialize the print environment
t, omega0, gamma = sympy.symbols("t, omega_0, gamma", positive=True)
## symbolize the parameters and they can only be positive
x = sympy.Function('x')
## set x to be the differential function, not the variable
ode = x(t).diff(t, 2) + 2 * gamma * omega0 * x(t).diff(t) + omega0**2*x(t)
ode_sol = sympy.dsolve(ode)
## use diff() and dsolve to get the general solution
ics = { 
   x(0): 1, x(t).diff(t).subs(t, 0): 0}
## apply dict to the initial conditions
x_t_sol = apply_ics(ode_sol, ics, t, [omega0, gamma])
## get the solution with ics by calling function apply_ics.
sympy.pprint(x_t_sol)
## pretty print
## solution is as follows
                                   ⎛       _______   _______⎞                 
       ⎛        γ         1⎞  ω₀⋅t⋅⎝-γ - ╲╱ γ - 1 ⋅╲╱ γ + 1 ⎠   ⎛      γ      
x(t) = ⎜- ───────────── + ─⎟⋅ℯ                                + ⎜─────────────
       ⎜       ________   2⎟                                    ⎜     ________
       ⎜      ╱  2         ⎟                                    ⎜    ╱  2     
       ⎝  2⋅╲╱  γ  - 1     ⎠                                    ⎝2⋅╲╱  γ  - 1 

            ⎛       _______   _______⎞
   1⎞  ω₀⋅t⋅⎝-γ + ╲╱ γ - 1 ⋅╲╱ γ + 1 ⎠
 + ─⎟⋅ℯ                               
   2⎟                                 
    ⎟                                 
    ⎠                                 

参考

1. [https://vlight.me/2018/05/01/Numerical-Python-Ordinary-Differential-Equations/]
2. [https://docs.sympy.org/latest/search.html?q=]

微分方程：python数值解(SciPY)

当ODE无法求得解析解时，可以用scipy中的integrate.odeint求数值解来探索其解的部分性质，并辅以可视化，能直观地展现ODE解的函数表达。
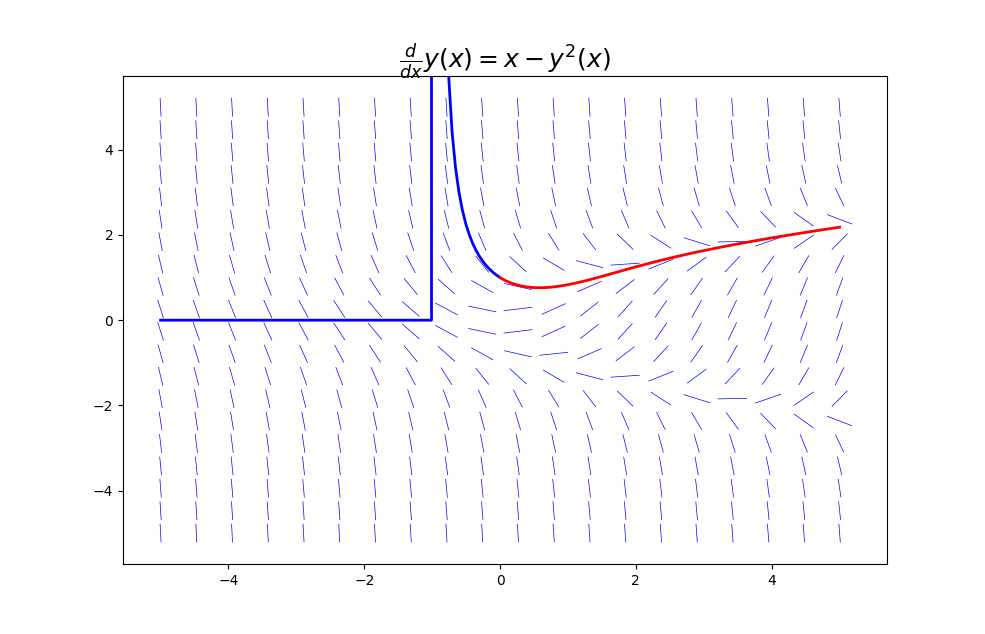
以如下一阶非线性（因为函数y幂次为2）ODE为例， $$\frac{dy}{dx}=x-y(x{)}^2.$$
现用odeint 求其数值解，代码与可视化如下。

import numpy as np
from scipy import integrate
import matplotlib.pyplot as plt
import sympy

def plot_direction_field(x, y_x, f_xy, x_lim=(-5, 5), y_lim=(-5, 5), ax=None):
    f_np = sympy.lambdify((x, y_x), f_xy, 'numpy')
    x_vec = np.linspace(x_lim[0], x_lim[1], 20)
    y_vec = np.linspace(y_lim[0], y_lim[1], 20)

    if ax is None:
        _, ax = plt.subplots(figsize=(4, 4))

    dx = x_vec[1] - x_vec[0]
    dy = y_vec[1] - y_vec[0]

    for m, xx in enumerate(x_vec):
        for n, yy in enumerate(y_vec):
            Dy = f_np(xx, yy) * dx
            Dx = 0.8 * dx**2 / np.sqrt(dx**2 + Dy**2)
            Dy = 0.8 * Dy*dy / np.sqrt(dx**2 + Dy**2)
            ax.plot([xx - Dx/2, xx + Dx/2], [yy - Dy/2, yy + Dy/2], 'b', lw=0.5)

    ax.axis('tight')
    ax.set_title(r"$%s$" %(sympy.latex(sympy.Eq(y_x.diff(x), f_xy))), fontsize=18)

    return ax

x = sympy.symbols('x')
y = sympy.Function('y')
f = x-y(x)**2

f_np = sympy.lambdify((y(x), x), f)
## put variables (y(x), x) into lambda function f.
y0 = 1
xp = np.linspace(0, 5, 100)
yp = integrate.odeint(f_np, y0, xp)
## solve f_np with initial conditons y0, and x ranges as xp.
xn = np.linspace(0, -5, 100)
yn = integrate.odeint(f_np, y0, xm)

fig, ax = plt.subplots(1, 1, figsize=(4, 4))
plot_direction_field(x, y(x), f, ax=ax)
## plot direction field of function f
ax.plot(xn, yn, 'b', lw=2)
ax.plot(xp, yp, 'r', lw=2)
plt.show()

右侧曲线跟方向场贴合一致，但左侧蓝线的数值解诡异，明显不满足ODE的表达式，这也说明数值解的局限性。

微分方程组：python数值解

以求解洛伦兹曲线为例，以下方程组代表曲线在xyz三个方向上的速度，给定一个初始点，可以画出相应的洛伦兹曲线。
$$\{\begin{array}{l}\frac{dx}{dt}=p(y-x),\\ \frac{dy}{dt}=x(r-z),\\ \frac{dz}{dt}=xy-bz,.\end{array}$$
代码与图如下。

import numpy as np
from scipy.integrate import odeint
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt

def dmove(Point, t, sets):
    """ point：present location index sets：super parameters """
    p, r, b = sets
    x, y, z = Point
    return np.array([p * (y - x), x * (r - z), x * y - b * z])


t = np.arange(0, 30, 0.001)
P1 = odeint(dmove, (0., 1., 0.), t, args=([10., 28., 3.],))  #
## (0.,1.,0.) is the initial point; args is the set for super parameters
P2 = odeint(dmove, (0., 1.01, 0.), t, args=([10., 28., 3.],))
## slightly change the initial point from y = 1.0 to be y = 1.01

fig = plt.figure()
ax = Axes3D(fig)
ax.plot(P1[:, 0], P1[:, 1], P1[:, 2])
ax.plot(P2[:, 0], P2[:, 1], P2[:, 2])
plt.show()

洛伦兹曲线很好地展示了非线性的直观形态，同时也是展示混沌系统的经典例子。这个例子告诉我们，混沌系统可以是一个确定系统，不一定是随机过程，同时它有初值敏感的特征。

参考
scipy.integrate.odeint用法