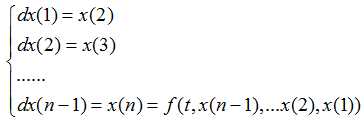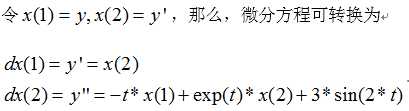matlab求解常微分方程（组）—dsolve、ode系列函数详解（含例程）

本文主要介绍matlab中求解常微分方程（组）的dsolve和ode系列函数，并通过例子加深读者的理解。

一、符号介绍

   D: 微分符号；D2表示二阶微分，D3表示三阶微分，以此类推。

二、函数功能介绍及例程

1、dsolve 函数

dsolve函数用于求常微分方程组的精确解，也称为常微分方程的符号解。如果没有初始条件或边界条件，则求出通解；如果有，则求出特解。

1)函数格式  

Y = dsolve(‘eq1,eq2,…’ , ’cond1,cond2,…’ , ’Name’)

其中，‘eq1,eq2,…’:表示微分方程或微分方程组;

            ’cond1,cond2,…’:表示初始条件或边界条件;

            ‘Name’:表示变量。没有指定变量时，matlab默认的变量为t；

2)例程

例1.1(dsolve 求解微分方程)

求解微分方程：

在命令行输入: dsolve(‘Dy=3*x^2′,’x’) ,摁下enter键后输出运行结果。

例1.2（加上初始条件）

求解微分方程：

只需要在命令行添加初始条件即可，此时求出的即为方程的特解。可以看到上例中的C9变为了2。

例2(dsolve 求解微分方程组)

求解微分方程组： 

由于x,y均为t的导数，所以不需要在末尾添加’t’。

2、ode函数

在上文中我们介绍了dsolve函数。但有大量的常微分方程，虽然从理论上讲，其解是存在的，但我们却无法求出其解析解，此时，我们需要寻求方程的数值解。

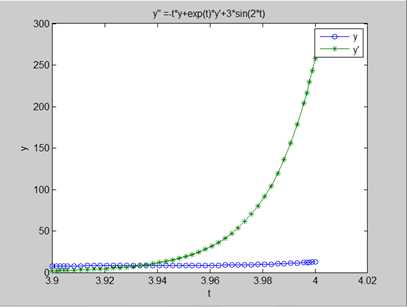
怎么理解数值求解呢？数值分析是一门专门的学科，在此不过多介绍。我主要想通过一个简单的例子来向大家阐述数值求解的思想。

比如，求解微分方程  。我们就可以转化为，那么。因此，我们可以通过迭代的方式来求解y。即可理解为步长

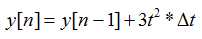
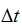
ode是Matlab专门用于解微分方程的功能函数。该求解器有变步长（variable-step）和定步长（fixed-step）两种类型。不同类型有着不同的求解器，具体说明如下图。 

其中，ode45求解器属于变步长的一种，采用Runge-Kutta算法；其他采用相同算法的变步长求解器还有ode23。ode45表示采用四阶–五阶Runge-Kutta算法，它用4阶方法提供候选解，5阶方法控制误差，是一种自适应步长（变步长）的常微分方程数值解法，其整体截断误差为(Δx)^5。解决的是Nonstiff(非刚性)常微分方程。

ode45是解决数值解问题的首选方法，若长时间没结果，应该就是刚性的，可换用ode15s试试。

下面将以ode45为例具体介绍函数的使用方法。

1)函数格式  

[T,Y] = ode45(‘odefun’,tspan,y0)

[T,Y] = ode45(‘odefun’,tspan,y0,options)

[T,Y,TE,YE,IE] = ode45(‘odefun’,tspan,y0,options)

sol = ode45(‘odefun’,[t0 tf],y0…)

其中: odefun是函数句柄,可以是函数文件名,匿名函数句柄或内联函数名；

          tspan 是求解区间 [t0 tf]，或者一系列散点[t0,t1,…,tf]；

          y0 是初始值向量

          T 返回列向量的时间点

          Y 返回对应T的求解列向量

          options 是求解参数设置,可以用odeset在计算前设定误差,输出参数,事件等

           TE 事件发生时间

           YE 事件发生时之答案

            IE 事件函数消失时之指针i

2)微分方程标准化

利用ode45求解高阶微分方程时，需要做变量替换。下面说明替换的基本思路。

微分方程为

初始条件

首先做变量替换 

原微分方程可以转换为下面的微分方程组的格式:

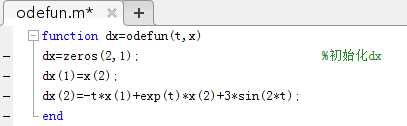
下面就可以利用转换好的微分方程组来编写odefun函数。

3）例程

例3.1（编写odefun函数）

在matlab中新建脚本文件，编写函数如下：

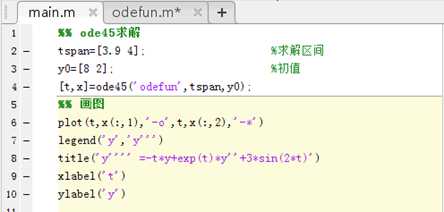
本例中只需在例3.1的基础上编写主函数，加上求解区间和边值条件即可。需要注意的是，ode45的运行结果以列向量形式给出。因此在本例中，x的第一列为y，第二列为y’。如果遇到变量不是列向量形式的，可以考虑利用reshape函数做矩阵变换。

则，plot(t,x(:,1))画出来的是x的第一列数据，即为y；

        plot(t,x(:,2))画出来的是x的第二列数据，即为y’；

三、总结

在使用matlab中，如遇到命令格式记不清楚等情况，建议直接在命令行输入指令’help+函数名称’，如，在matlab命令窗口输入help dsolve后，显示如下：

参考：

1、https://jingyan.baidu.com/article/e52e36154448e940c60c51aa.html

2、https://baike.baidu.com/item/ode45/6674723?fr=aladdin

3、https://wenku.baidu.com/view/45a0a0b54b73f242326c5f7f.html