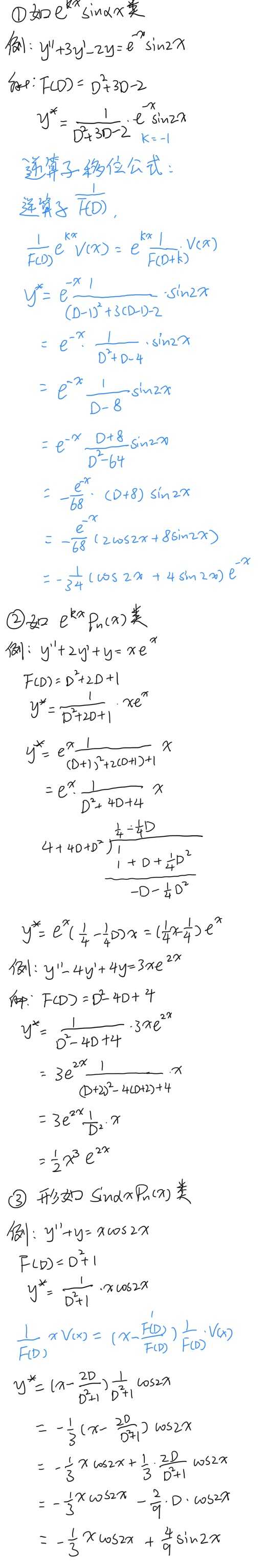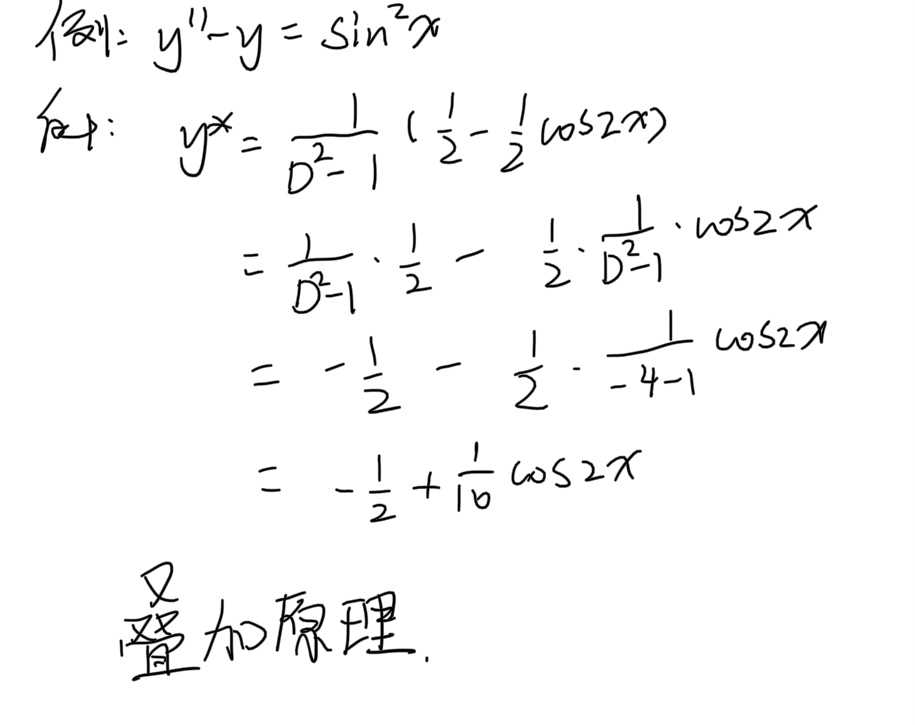文章目录
欢迎纠错
#微分算子法 D 求特解
##概述
y ′ = d d x ( y ) = D y y ′ ′ = D 2 y D : 微 分 算 子 , 代 表 求 导 ; 1 D 代 表 积 分 n 阶 微 分 方 程 基 本 形 式 : a n D n y + a n − 1 D n − 1 y + ⋯ + a 1 D y + a 0 y = f ( x ) ( a n D n + a n − 1 D n − 1 + ⋯ + a 1 D + a 0 ) y = f ( x ) F ( D ) y = f ( x ) y = 1 F ( D ) f ( x ) y’=\frac{d}{dx}(y)=Dy\\\ \\ y”=D^2y\\\ \\ D:微分算子,代表求导;\frac 1 D 代表积分\\\ \\ n阶微分方程基本形式:\\\ \\ a_nD^ny+a_{n-1}D^{n-1}y+\cdots+a_{1}Dy+a_0y=f(x)\\\ \\ (a_nD^n+a_{n-1}D^{n-1}+\cdots+a_{1}D+a_0)y=f(x)\\\ \\ F(D)y=f(x)\\\ \\ y=\frac{1}{F(D)}f(x) y′=dxd(y)=Dy y′′=D2y D:微分算子,代表求导;D1代表积分 n阶微分方程基本形式: anDny+an−1Dn−1y+⋯+a1Dy+a0y=f(x) (anDn+an−1Dn−1+⋯+a1D+a0)y=f(x) F(D)y=f(x) y=F(D)1f(x)
## f ( x ) f(x) f(x)为 e k x e^{kx} ekx型
## f ( x ) f(x) f(x)为 sin α x ( cos α x ) \sin\alpha x (\cos \alpha x) sinαx(cosαx)型
## f ( x ) f(x) f(x)为 P n ( x ) P_n(x) Pn(x)型
##三种混合型
##其他一些例子
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/38311.html