linux终端解微分方程,解微分方程+ode求解器

该命令中可以用D表示微分符号，其中D2表示二阶微分，D3表示三阶微分，以此类推。

求精确解

1.微分方程

r=dsolve(‘eqn1′,’eqn2′,…,’cond1′,’cond2′,…,’var’).

解释如下：eqni表示第i个微分方程，condi表示第i个初始条件，var表示微分方程中的自变量，默认为t。

>> dsolve(‘Dy=3*x^2′,’y(0)=2′,’x’)

ans =

x^3 + 2

2.微分方程组

>> [x,y]=dsolve(‘Dx=y’,’D2y-Dy=0′,’x(0)=2′,’y(0)=1′,’Dy(0)=1′)

x =

exp(t) + 1

y =

exp(t)

3.求解微分方程组

在初始条件x(t=0)=1,y(t=0)=0下的特解,并画出解函数的图像。

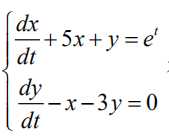
>> [x,y]=dsolve(‘Dx+5*x+y=exp(t)’,’Dy-x-3*y=0′,’x(0)=1′,’y(0)=0′,’t’)

x =

exp(t*(15^(1/2) – 1))*(15^(1/2) – 4)*((13*15^(1/2))/330 – exp(2*t – 15^(1/2)*t)*(15^(1/2)/165 + 1/22) + 1/22) – exp(-t*(15^(1/2) + 1))*(exp(2*t + 15^(1/2)*t)*(15^(1/2)/165 – 1/22) + (15^(1/2)*(15^(1/2) – 13))/330)*(15^(1/2) + 4)

y =

exp(-t*(15^(1/2) + 1))*(exp(2*t + 15^(1/2)*t)*(15^(1/2)/165 – 1/22) + (15^(1/2)*(15^(1/2) – 13))/330) + exp(t*(15^(1/2) – 1))*((13*15^(1/2))/330 – exp(2*t – 15^(1/2)*t)*(15^(1/2)/165 + 1/22) + 1/22)

>> ezplot(x,y)

ezplot与plot的区别

plot(x,y)以x为横坐标，y为纵坐标绘制曲线

plot(x,y1,x,y2,…)以x为横坐标值，以y1，y2…元素为纵坐标值绘制多条曲线

plot中x,y的表达式是已知的或者是形如y=f(x)的表达式

而ezplot是画出隐函数图形，是形如f(x,y)=0这种不能写出像y=f(x)这种函数的图形，explot无需数据准备，直接画出函数图形

求近似解

ode求解器

求解器

问题类型

精度

何时使用

非刚性

中

大多数情况下，您应当首先尝试求解器 ode45。

低

对于容差较宽松的问题或在刚度适中的情况下，ode23 可能比 ode45 更加高效。

低到高

对于具有严格误差容限的问题或在 ODE 函数需要大量计算开销的情况下，ode113 可能比 ode45 更加高效。

刚性

低到中

若 ode45 失败或效率低下并且您怀疑面临刚性问题，请尝试 ode15s。此外，当解算微分代数方程 (DAE) 时，请使用 ode15s。

低

对于误差容限较宽松的问题，ode23s 可能比 ode15s 更加高效。它可以解算一些刚性问题，而使用 ode15s 解算这些问题的效率不高。

ode23s 会在每一步计算 Jacobian，因此通过 odeset 提供 Jacobian 有利于最大限度地提高效率和精度。

如果存在质量矩阵，则它必须为常量矩阵。

低

对于仅仅是刚度适中的问题，并且您需要没有数值阻尼的解，请使用 ode23t。

ode23t 可解算微分代数方程 (DAE)。

低

与 ode23s 一样，对于误差容限较宽松的问题，ode23tb 求解器可能比 ode15s 更加高效。

完全隐式

低

对于完全隐式问题 f(t,y,y’) = 0 和微分指数为 1 的微分代数方程 (DAE)，请使用 ode15i。

1. 求解微分方程初值问题

的数值解，求解范围为区间 [0,0.5] 。

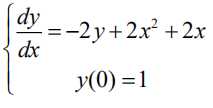
inline()通俗的来说就是用于定义函数，使用inline定义一个函数

给a，b，x赋值即可得到y

>> f=inline(‘a*x+b’,’a’,’b’,’x’);

>> f(1,2,3)

ans =

5

求常微分方程的数值解，MATLAB的命令格式为：

[t,y]=solver(‘odefun’,tspan,y0,options)

其中solver选择ode45等函数名，odefun为根据待解方程或方程组编写的m文件名，tspan为自变量的区间[t0,tf]，即准备在那个区间上求解，y0表示初始值，options用于设定误差限制。命令格式为：

options=odeset(‘reltol’,rt,’abstol’,at)

rt输入相对误差，at输入绝对误差。