matlab画三维图像（plot3,mesh,surf）

二维函数的图像必须用三维坐标系画，很多函数的图像长得很好看，很有意思。会可视化也会有利于我们理解更深刻。

（1）plot3,三维曲线图

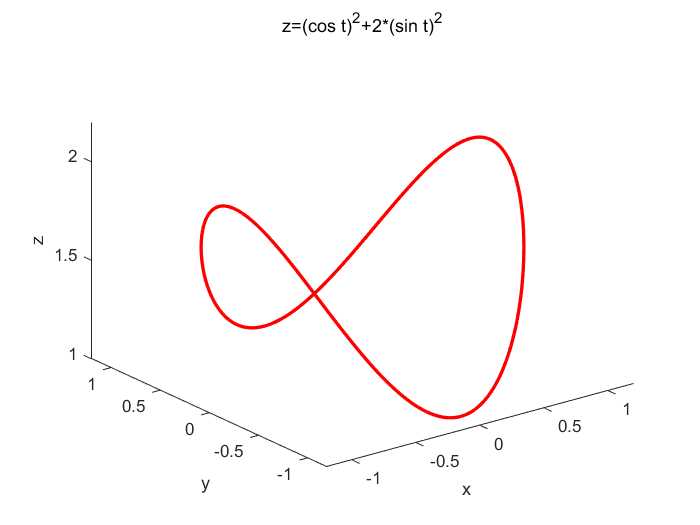
在网上看到这图觉得挺好看：

t=0:pi/360:2*pi;
x=sin(t);
y=cos(t);
z=2*x.^2+y.^2;
figure
plot3(x,y,z,'Color','r','LineWidth',2);
xlabel('x');
ylabel('y');
zlabel('z');
title('z=(cos t)^2+2*(sin t)^2');
axis([-1.2 1.2 -1.2 1.2 1 2.2]);

（2）mesh,网面图

clear all,clc;
t=-0.5:.01:0.5;
[x,y]=meshgrid(t);%形成格点矩阵
z=sin(4*pi*x)+cos(6*pi*y);
figure(1)
mesh(x,y,z);
axis([-0.5 0.5 -0.5 0.5 -2 2]);
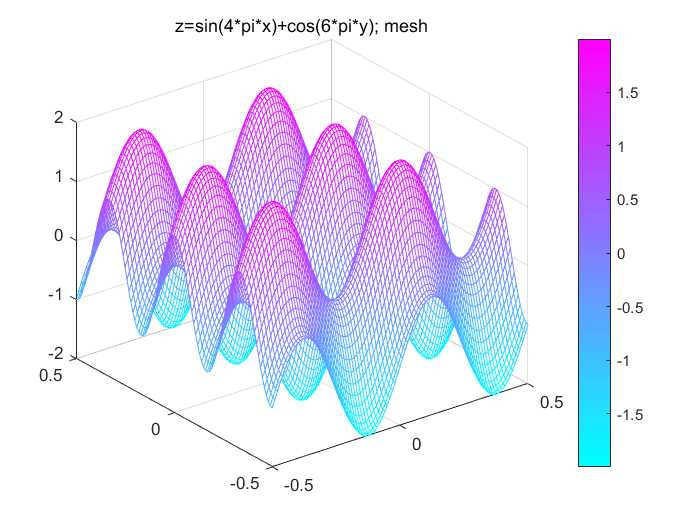
title('z=sin(4*pi*x)+cos(6*pi*y); mesh')
colormap cool%cool是一种配色方案，还有其他方案如winter，summer····见help colormap
colorbar

画个二元函数，观察采样后频谱的混叠现象

二元函数图像的绘制还是把变量分为多个离散点绘制，只是增大点数。

clear all,clc;
t=-1:.01:1;
[x,y]=meshgrid(t);%形成格点矩阵
f=cos(2*pi*(2*x-y));
figure(1)
mesh(x,y,f);grid on
xlabel('x');
ylabel('y');
zlabel('f');
axis([-0.5 0.5 -1 1 -1.5 1.5]);
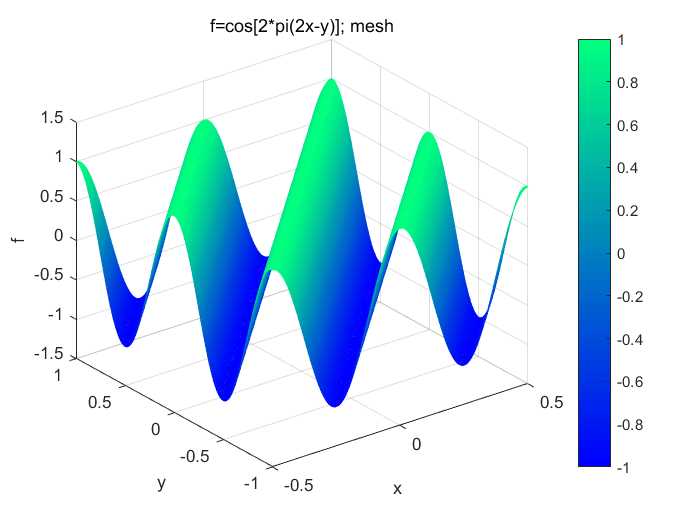
title('f=cos[2*pi(2x-y)]; mesh')
colormap winter
colorbar

先手动计算一下它的二位傅里叶变换：
不想打公式（逃）

F= fft2(f);%做二维DFT变换，把连续函数取样得到一个矩阵，把这个矩阵当图像一样处理
figure(2)
subplot(121),imshow(abs(F),[]);title('函数f=cos(2*pi(2x-y))二维频谱')
F=fftshift(F);%使用matlab的fftshift函数把低频分量移到频谱中心
subplot(122),imshow(abs(F),[]);title('中心化频谱')

t=-1.1:.333:1.1;%以频率3采样（题目要求）
[x,y]=meshgrid(t);%形成格点矩阵
f=cos(2*pi*(2*x-y));
figure(1)
mesh(x,y,f);grid on
xlabel('x');
ylabel('y');
zlabel('f');
axis([-1 1 -1 1 -1.5 1.5]);
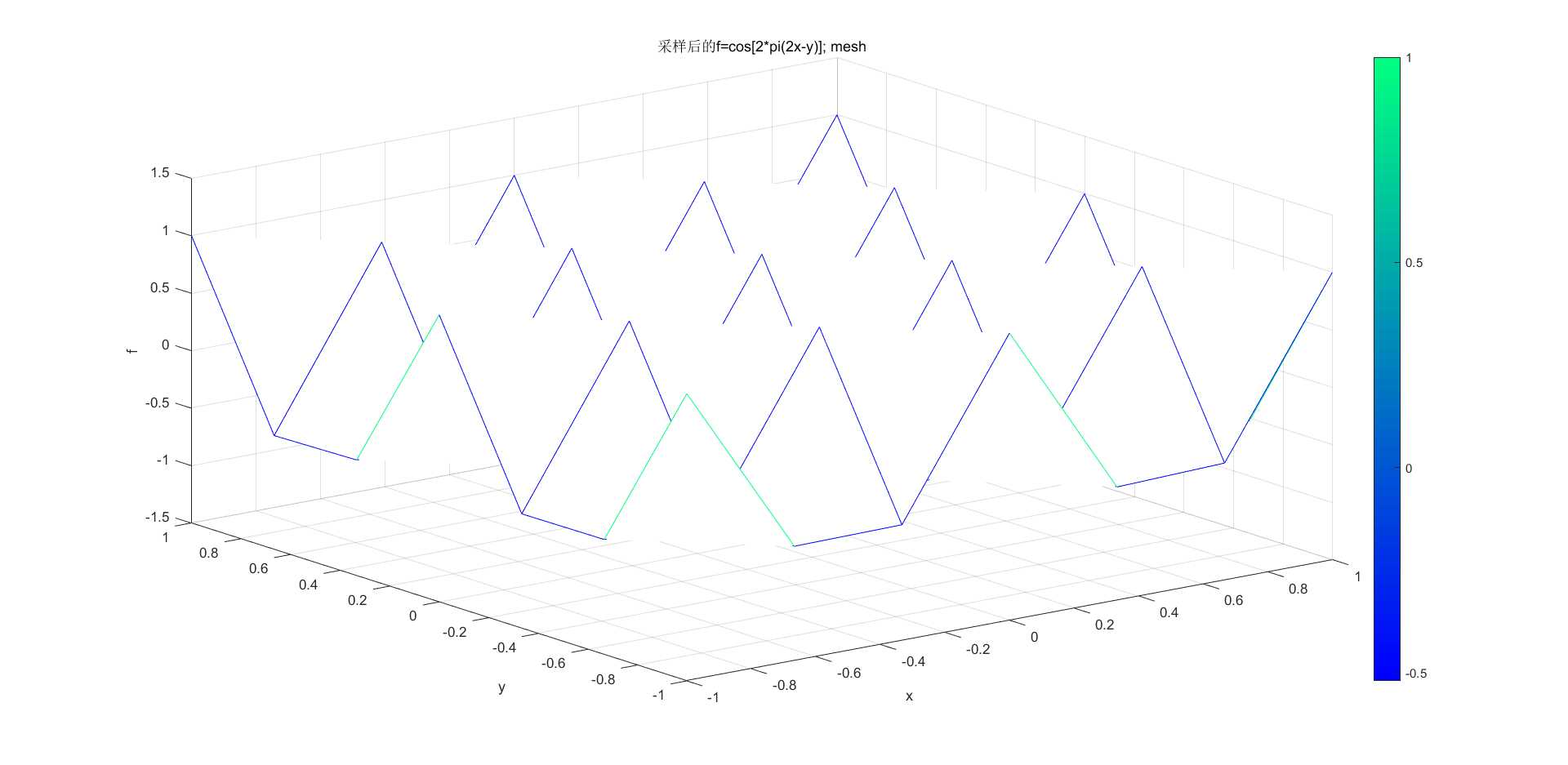
title('采样后的f=cos[2*pi(2x-y)]; mesh')
colormap winter
colorbar

F= fft2(f);%做二维DFT变换，把连续函数取样得到一个矩阵，把这个矩阵当图像一样处理
figure(2)
subplot(121),imshow(abs(F),[]);title('函数f=cos(2*pi(2x-y))采样后的二维频谱')
F=fftshift(F);%使用matlab的fftshift函数把低频分量移到频谱中心
subplot(122),imshow(abs(F),[]);title('中心化频谱')

采样后信号：

采样后信号频谱：
函数的x方向频率是2，y方向频率是1，所以一定会有混叠失真
可以看出频谱的能量中心的相对位置都不对，这就是混叠失真引起的

t=-1.1:.17:1.1;%以更高频率采样
[x,y]=meshgrid(t);%形成格点矩阵
f=cos(2*pi*(2*x-y));
figure(1)
mesh(x,y,f);grid on
xlabel('x');
ylabel('y');
zlabel('f');
axis([-1 1 -1 1 -1.5 1.5]);
title('采样后的f=cos[2*pi(2x-y)]; mesh')
colormap winter
colorbar

F= fft2(f);%做二维DFT变换，把连续函数取样得到一个矩阵，把这个矩阵当图像一样处理
figure(2)
subplot(121),imshow(abs(F),[]);title('函数f=cos(2*pi(2x-y))采样后的二维频谱')
F=fftshift(F);%使用matlab的fftshift函数把低频分量移到频谱中心
subplot(122),imshow(abs(F),[]);title('中心化频谱')

以更大的采样频率采样，避免不满足奈奎斯特定理产生混叠：
可见得到的频谱和连续函数的频谱更相似。采样频率越大，得到的频谱和连续函数的频谱越相似