文章目录
- 0 前言
- 1 plot3函数
-
- 1.1 plot3函数的基本用法
- 1.2 plot3(x,y,z)函数参数的变化形式
- 1.3 含多组输入参数的plot3函数
- 1.4 含选项的plot3函数
- 2 fplot3函数
-
- 2.1 fplot3函数的基本用法
- 2.2 练习
- 3 结语
0 前言
本文是科学计算与MATLAB语言的专题四的第四小节总结笔记,并结合了自己一点的理解,看完本文,可以轻松利用MATLAB的plot3函数和fplot函数,画出三维曲线。
1 plot3函数
1.1 plot3函数的基本用法
plot3(x,y,z)
其中
参数x、y、z组成一组曲线的坐标。
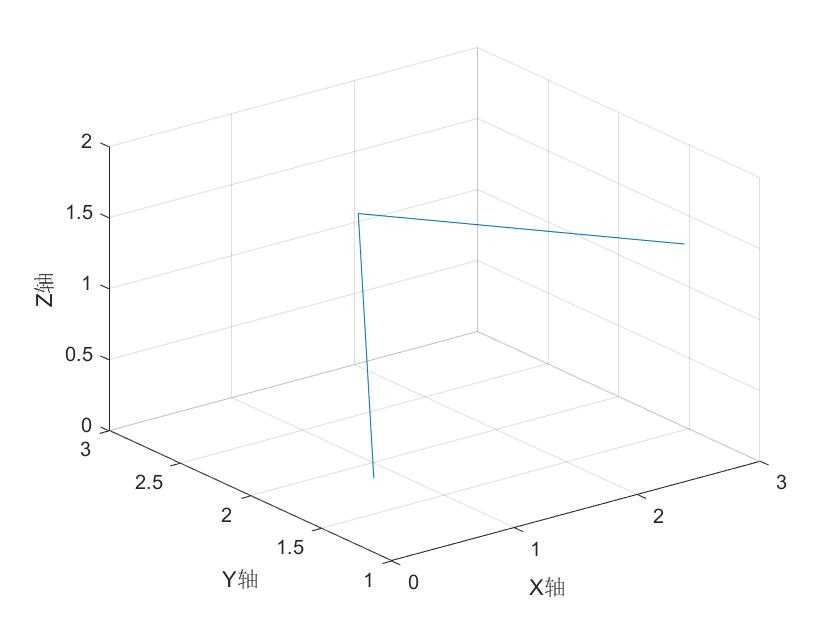
例1 绘制一条空间折线。
x=[0.2, 1.8, 2.5];
y=[1.3, 2.8, 1.1];
z=[0.4, 1.2, 1.6];
plot3(x, y, z)
grid on
axis([0, 3, 1, 3, 0, 2]);
xlabel({'X轴'});
zlabel({'Z轴'});
ylabel({'Y轴'});
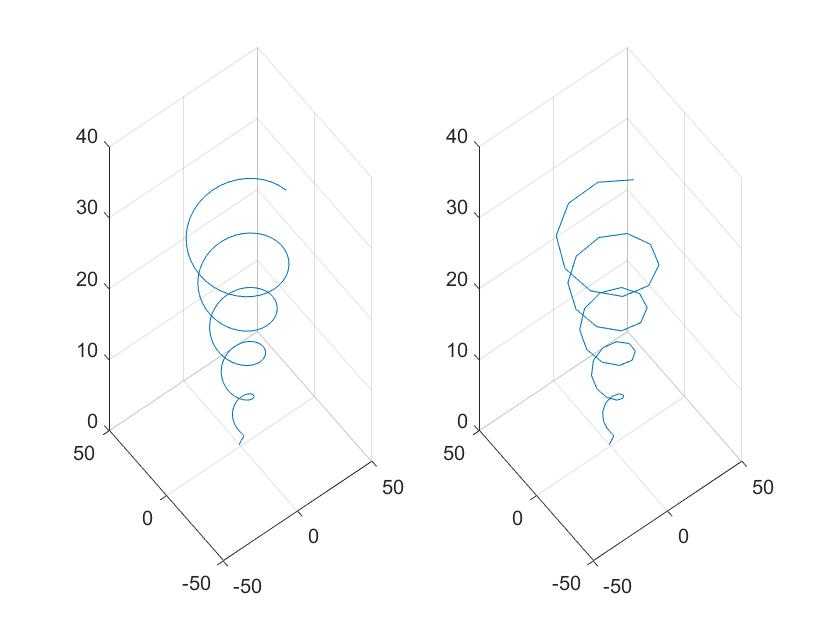
例2 绘制螺旋线 { x = s i n ( t ) + t c o s ( t ) y = c o s ( t ) − t s i n ( t ) ( 0 ≤ t ≤ 10 π ) z = t \left\{\begin{aligned} x&=sin(t)+tcos(t)\\ y&=cos(t)-tsin(t)(0 \leq t\leq10\pi)\\ z&=t \end{aligned}\right. ⎩⎪⎨⎪⎧xyz=sin(t)+tcos(t)=cos(t)−tsin(t)(0≤t≤10π)=t
t=linspace(0, 10*pi, 200);
x=sin(t)+t.*cos(t);%''.*'',按两个矩阵每个对应位置元素相乘形成的一个新矩阵
y=cos(t)-t.*sin(t);
z=t;
subplot(1, 2, 1)
plot3(x, y, z)
grid on
subplot(1, 2, 2)
plot3(x(1:4:200), y(1:4:200), z(1:4:200))%点的间隔变大,曲线没有图一光滑。
grid on
1.2 plot3(x,y,z)函数参数的变化形式
plot3(X,Y,Z)
参数X、Y、Z是同型矩阵时,以X、Y、Z对应列元素绘制曲线,曲线条数等于矩阵列数。
参数X、Y、Z中有向量,也有矩阵时,向量的长度应与矩阵相符。
向量指的是m×1的行向量,或1×n的列向量
被绕晕了吗?看以下示例。
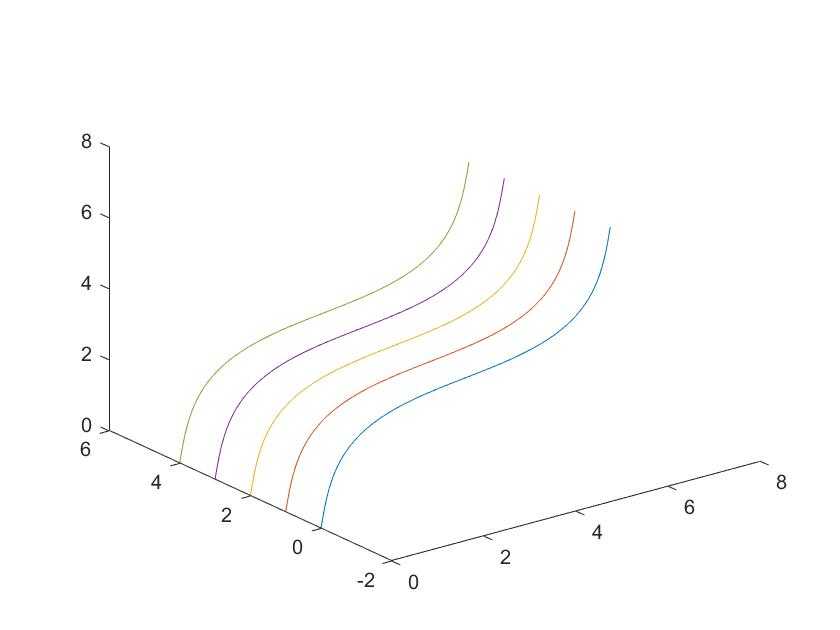
例3 在空间不同位置绘制5条正弦曲线。
t=0:0.01:2*pi;
t=t';
x=[t, t, t, t, t];
y=[sin(t), sin(t)+1, sin(t)+2, sin(t)+3, sin(t)+4];
z=x;
%这里x、y、z都是一个629×5的同型矩阵,所以曲线的条数为5。
plot3(x,y,z)
这个例子也可以采用以下代码实现。
t=0:0.01:2*pi;
x=t;
y=[sin(t); sin(t)+1; sin(t)+2; sin(t)+3; sin(t)+4];
z=x;
plot3(x,y,z)
1.3 含多组输入参数的plot3函数
plot3(x1,y1,z1,×2,y2,z2,…,xn,yn,zn)
每一组x、y、z向量构成一组数据点的坐标,绘制一条曲线。
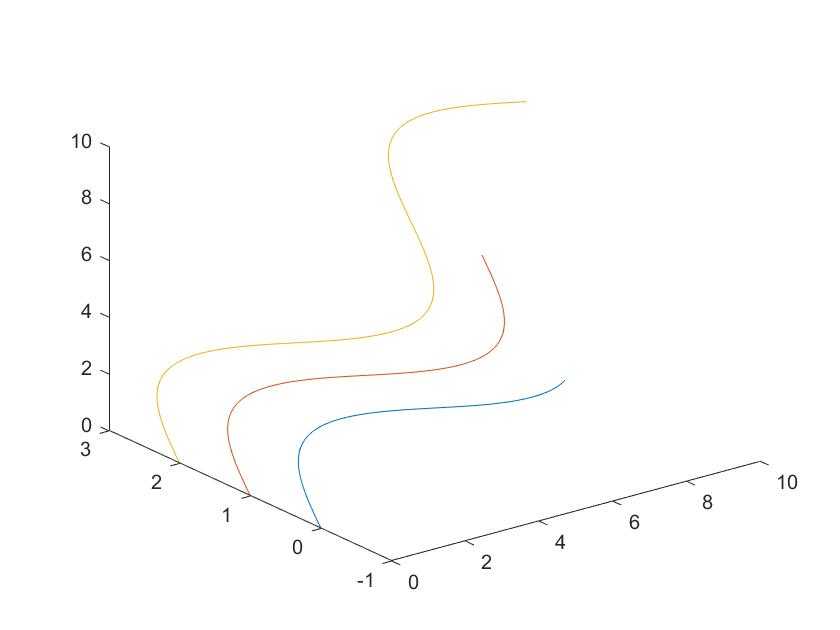
例4 绘制三条不同长度的正弦曲线。
t1=0:0.01:1.5*pi;
t2=0:0.01:2*pi;
t3=0:0.01:3*pi;
plot3(t1,sin(t1),t1, t2,sin(t2)+1,t2, t3,sin(t3)+2,t3)
1.4 含选项的plot3函数
plot3(x,y,z,选项)
选项用于指定曲线的线型、颜色和数据点标记。
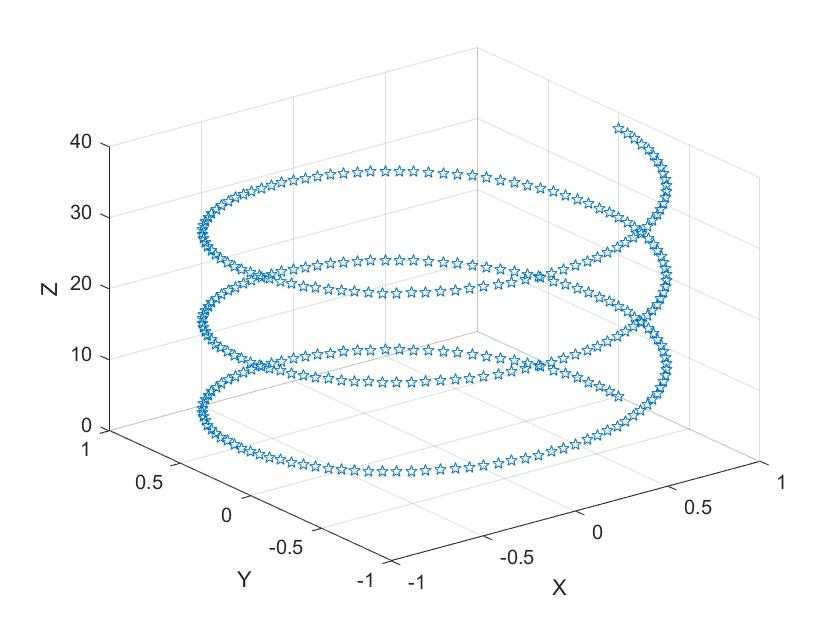
例5 绘制空间曲线 { x = c o s ( t ) y = s i n ( t ) ( 0 ≤ t ≤ 6 π ) z = 2 t \left\{ \begin{aligned} x&=cos(t)\\ y&=sin(t)(0\leq t \leq6\pi)\\ z&=2t \end{aligned}\right. ⎩⎪⎨⎪⎧xyz=cos(t)=sin(t)(0≤t≤6π)=2t
t=0:pi/50:6*pi;
x=cos(t);
y=sin(t);
z=2*t;
plot3(x,y,z,'p')
xlabel('X'),ylabel('Y'),zlabel('Z');
grid on
2 fplot3函数
2.1 fplot3函数的基本用法
fplot3(funx,funy,funz,tlims)
其中
funx、funy、funz代表定义曲线x、y、z坐标的函数,通常采用函数句柄的形式。
tlims为参数函数自变量的取值范围,用二元向量[tmin,tmax]描述,默认为[-5,5]。
2.2 练习
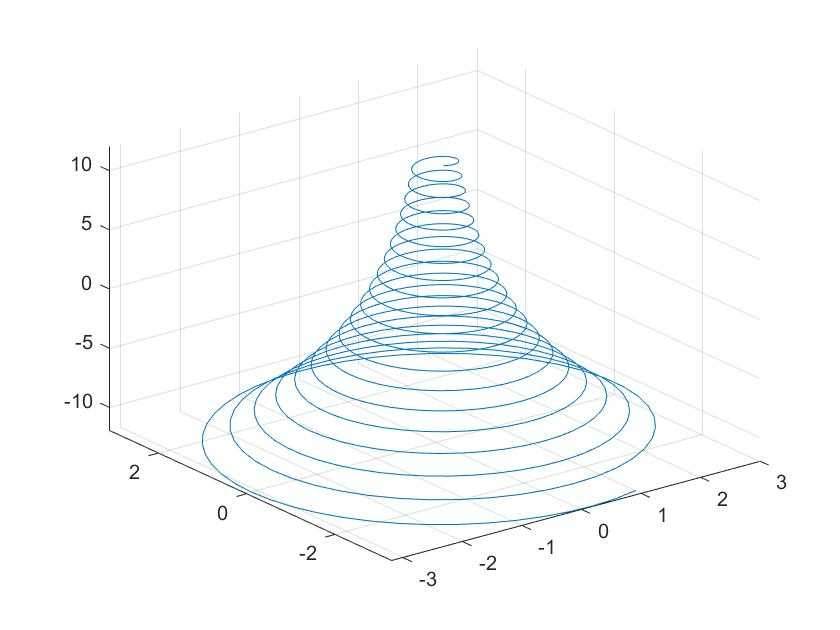
例6 绘制墨西哥帽顶曲线 { x t = e − t 10 s i n ( 5 t ) y t = e − t 10 c o s ( 5 t ) ( − 12 ≤ t ≤ 12 ) z t = t \left\{ \begin{aligned} x_t &= e^{-\frac{t}{10}sin(5t)}\\ y_t &= e^{-\frac{t}{10}cos(5t)}(-12\leq t \leq12)\\ z_t&= t \end{aligned}\right. ⎩⎪⎪⎨⎪⎪⎧xtytzt=e−10tsin(5t)=e−10tcos(5t)(−12≤t≤12)=t
xt = @(t) exp(-t/10).*sin(5*t);
yt = @(t) exp(-t/10).*cos(5*t);
zt = @(t) t;
fplot3(xt, yt, zt, [-12, 12])
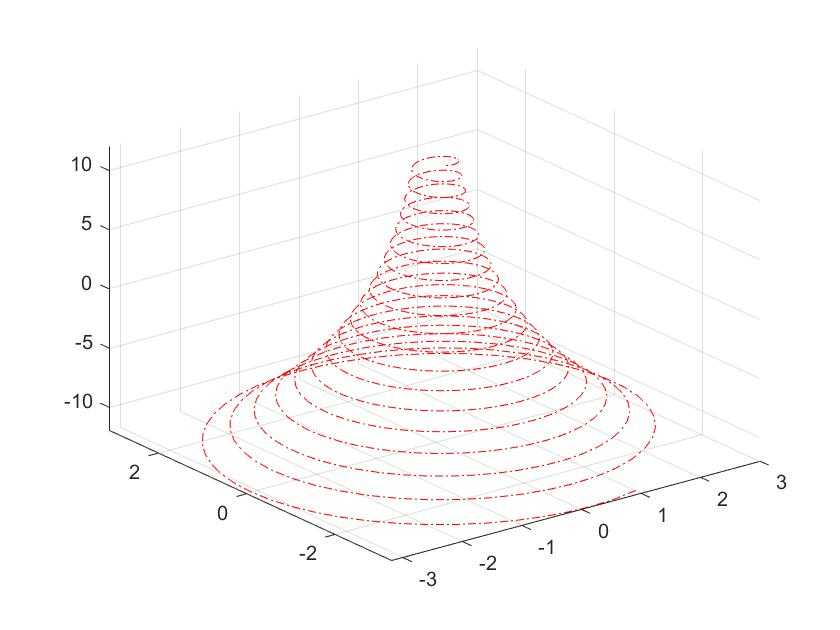
用红色点划线绘制墨西哥帽顶曲线。
xt = @(t) exp(-t/10).*sin(5*t);
yt = @(t) exp(-t/10).*cos(5*t);
zt = @(t) t;
fplot3(xt, yt, zt, [-12, 12], 'r-.')
3 结语
如果本文对您有帮助,可以点个赞哈,如有错误疑问,请您指出哈。
今天的文章matlab中绘制三维曲线图的函数_plot绘图「建议收藏」分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/57904.html