c语言枚举法经典例题_c语言中定义单精度实型变量「建议收藏」

摘要：在运筹学中利用经典的单纯形法人工求解线性规划问题较为复杂，但利用计算机强大的计算能力便能够快速实现。本文利用经典的单纯形法的算法，借助传统的C语言进行实现，大大提高了适用于单纯形法的线性规划问题的运算效率。

Absrtact: in operations research, it is more complex to solve the linear programming problem by using the classical simplex method, but it can be realized quickly by using the powerful computing power of the computer. In this paper, the classical simplex algorithm is used to implement with the help of traditional C language, which greatly improves the operation efficiency of linear programming problems suitable for simplex method.
关键词：单纯形法 线性规划 C语言
一、引言
运筹学的主要目的是在决策时为管理人员提供科学依据，是实施有效管理、正确决策和现代化管理的重要方法之一，常用于解决现实中的复杂问题，尤其是改善或优化现有系统的效率。对于小规模问题，可以通过较为简单的人工计算得到答案，但对于大规模问题，便需要借助计算机强大的计算能力来完成，所以研究计算机在线性规划中的应用很有实践意义，本文仅仅是管中窥豹，出于对C语言的一些兴趣，利用经典的单纯形法的算法，借助传统的C语言进行实现，大大提高了适用于单纯形法的线性规划问题的运算效率。
二、单纯形法算法原理
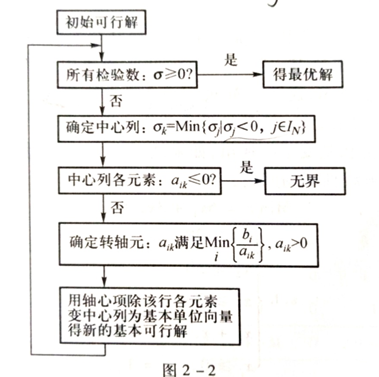
线性规划问题中，若存在最优解那么一定在某个基本可行解处取得，而我们可以将所有基本可行解找出来，代入目标函数后找到最优解，但是随着问题规模的增大，寻找所有基本可行解就变得异常困难。1947年G.B.Bantzig提出了单纯形法，成为了求解线性规划问题的基本方法。即先找到一个基本可行解，判断是否为最优解，若不是，从该可行解出发，寻找另一个基本可行解，再进行最优性判断，经此有限次步骤后便能够找到LP的最优解。

参考文献
[1]于松南.长春工业大学运筹学课程设计[Z]. https://wenku.baidu.com/view/4380168552ea551811a6872f.html,2015.
[2]尚有林.运筹学（第一版）[M]. 北京：高等教育出版社,2001.

#include <stdio.h>
#include <math.h>
#pragma warning(disable:4996)
#define m 3 //定义约束方程个数
#define n 5 //定义决策变量个数
double M = 1e6;
double A[m][n];		//存储A约束矩阵
double C[n];		//存储目标函数价值系数C矩阵
double b[m];		//存储约束条件资源系数b矩阵
double CB[m];		//存储基变量系数矩阵
double seta[m];		//存放出基和入基的变化情况
double sigma[n];	//存储检验数矩阵σ
double x[n];		//存储决策变量
int num[m];			//存储出基和入基变量的情况
double Z = 0;		//记录目标函数值

void input();
void print();
int FindSwapInVar();		//确定入基变量
int FindSwapOutVar(int a);	//确定出基变量
void Iterate(int a, int b);	//换基迭代

//确定入基变量，对于所有检验数均大于等于0时，当前解为最优解
int FindSwapInVar()
{ 
   
	int i, k = 0;//用k带出入基变量
	int flag = 1;
	double min = 0;
	for (i = 0; i < n; i++)
	{ 
   
		if (sigma[i] < 0)
		{ 
   
			flag = 0; break;
		}
	}
	if (flag == 1)//找到了咯
		return -1;
	for (i = 0; i < n; i++)//找出最大的检验数σ
	{ 
   
		if (sigma[i] < min)//求min问题按照sigma最小的为入基变量
		{ 
   
			min = sigma[i];
			k = i;
		}
	}
	return k;
}
//确定出基变量
int FindSwapOutVar(int a)
{ 
   
	int i, j;
	int flag = 1;
	int k = a;//a入基变量
	for (i = 0; i < m; i++)//如果某个数小于0的检验数，对应的列向量中所有元素≤0 该问题有无界解
	{ 
   
		if (A[i][k] > 0)
		{ 
   
			flag = 0; break;
		}
	}
	if (flag == 1)
	{ 
   
		printf("该线性规划问题有无界解、无最优解！\n");
		return -1;
	}
	for (i = 0; i < m; i++)
	{ 
   
		if (A[i][k] > 0)
			seta[i] = b[i] / A[i][k];
		else seta[i] = M;//当A[i][k]≤0的时候是不需要考虑的
		//然而是根据比值最小原则整的 所以给对应的卡一个很大的M
	}
	double min = M;
	for (i = 0; i < m; i++)//得到换出变量
	{ 
   
		if (min >= seta[i])
		{ 
   
			min = seta[i];
			j = i;
		}
	}
	num[j] = k + 1;
	CB[j] = C[k];
	return j;
}
//迭代运算，计算新的单纯形表
void Iterate(int p, int q)
{ 
   
	int i, j, r, c;//row行 column列（r,l)就是转轴元
	r = p;//行号 p是出基变量
	c = q;//列号 q是入基变量
	double temp1 = A[r][c];
	double temp2, temp3;
	//标准化该行
	b[r] /= temp1;
	for (j = 0; j < n; j++)
		A[r][j] /= temp1;
	for (i = 0; i < m; i++)//标准化其他行
	{ 
   
		if (i != r)
			if (A[i][c] != 0)
			{ 
   
				temp2 = A[i][c];
				b[i] -= temp2 * b[r];//b[r]转轴元对应b
				for (j = 0; j < n; j++)
					A[i][j] -= temp2 * A[r][j];//A[r][j]是转轴元对应行
			}
	}
	//σ的迭代计算
	temp3 = sigma[c];
	for (i = 0; i < n; i++)
	{ 
   
		sigma[i] -= A[r][i] * temp3;
	}

}
//输入函数、约束条件的技术系数矩阵A、初始基变量的数字代码
//输入约束条件的资源系数b、目标函数价值系数C
void input()
{ 
   
	int i, j;
	printf("请按顺序输入方程组的系数矩阵A（共%d行%d列）:\n", m, n);
	for (i = 0; i < m; i++)
		for (j = 0; j < n; j++)
			scanf("%lf", &A[i][j]);
	printf("请按顺序输入初始基变量所在列数的数字代码num矩阵：\n");
	for (i = 0; i < m; i++)
		scanf("%d", &num[i]);
	printf("请按顺序输入约束条件的资源系数b矩阵：\n");
	for (i = 0; i < m; i++)
		scanf("%lf", &b[i]);
	printf("请按顺序输入目标函数的价值系数C矩阵：\n");
	for (i = 0; i < n; i++)
		scanf("%lf", &C[i]);
	for (i = 0; i < n; i++)
		sigma[i] = C[i];
	for (i = 0; i < m; i++)
		CB[i] = C[num[i] - 1];//表示基变量的系数，因为将人类输入的转化为数组序号
}
//输出
void print()
{ 
   
	int i, j;
	printf("\n--------------------------------------------------------------------------\n");
	for (i = 0; i < m; i++)
	{ 
   
		printf("%8.2f\tX(%d) %8.2f ", CB[i], num[i], b[i]);
		for (j = 0; j < n; j++)
			printf("%8.2f ", A[i][j]);
		if (i != m - 1)
			printf("\n");
	}
	printf("\n--------------------------------------------------------------------------\n");
	printf("\t\t σ ");
	for (i = 0; i < n; i++)
		printf(" %8.2f", sigma[i]);
	printf("\n--------------------------------------------------------------------------\n");
}
int main()
{ 
   
	int i, j, k = 1;
	int p, q;//q是换入变量
	input();
	printf("\n--------------------------------------------------------------------------\n");
	printf("\tCB\tXB\tb\t");
	for (i = 0; i < n; i++)
		printf(" X(%d)\t", i + 1);
	for (i = 0; i < n; i++)
		x[i] = 0;
	while (true)
	{ 
   
		q = FindSwapInVar();
		if (q == -1)
		{ 
   
			print();
			printf("\n恭喜您得到最优解！\n");
			printf("最有解为：");
			for (j = 0; j < m; j++)
				x[num[j] - 1] = b[j];//因为x[n]对应第n+1个决策变量
			for (i = 0; i < n; i++)
			{ 
   
				printf("x%d=%.2f ", i + 1, x[i]);
				Z = Z + x[i] * C[i];
			}
			printf("\n最优值为：Z* = %.2f", Z);
			break;
		}
		print();
		p = FindSwapOutVar(q);
		printf("\n进行第%d次迭代,迭代元位置为(%d,%d)\n", k++, p + 1, q + 1);
		if (q == -1) break;
		Iterate(p, q);
	}
}
// momentum

今天的文章c语言枚举法经典例题_c语言中定义单精度实型变量「建议收藏」分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。