分析按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。如果在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
用 最小二乘法估计参数b,设服从正态分布,分别求对a、b
的偏导数并令它们等于零,得方程组解为
其中 ,且为观测值的 样本方差. 线性方程称为关于的线性回归方程,称为 回归系数,对应的直线称为 回归直线.顺便指出,将来还需用到,其中为观测值的样本方差.
先求x,y的平均值
X,Y
X,Y
再用公式代入求解:b=(x
1y
1+x
2y
2+…x
ny
n-n
XY)/(x
1
2+x
2
2+…x
n
2-n
X
2)
1y
1+x
2y
2+…x
ny
n-n
XY)/(x
1
2+x
2
2+…x
n
2-n
X
2)
后把x,y的平均数
X,Y代入a=
Y-b
X
X,Y代入a=
Y-b
X
求出a并代入总的公式
y=bx+a得到线性回归方程
y=bx+a得到线性回归方程
(X为xi的 平均数,Y为yi的平均数)
Python sklearn中的LinearRegreesion实例
import pandas as pd
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import numpy as np
#数据数据为两列数据x和y,有表头
df = pd.read_table('d:/LinearRegression.txt')
#通过pandas读取为DataFrame,回归用的是矩阵数据而不是列表,数据为n个样品点和m个特征值,这里特征值只有一个因此换证nx1的矩阵
dataSet_x = df.loc[:, 'X'].as_matrix(columns=None)
#T为矩阵转置把1xn变成nx1
dataSet_x = np.array([dataSet_x]).T
dataSet_y = df.loc[:, 'Y'].as_matrix(columns=None)
dataSet_y = np.array([dataSet_y]).T
#regr为回归过程,fit(x,y)进行回归
regr = LinearRegression().fit(dataSet_x, dataSet_y)
#输出R的平方
print(regr.score(dataSet_x, dataSet_y))
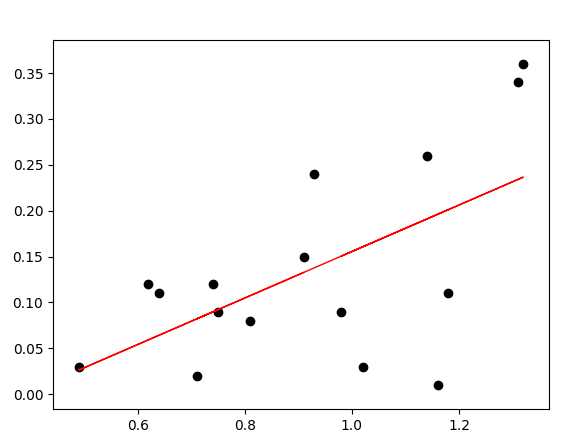
plt.scatter(dataSet_x, dataSet_y, color='black')
#用predic预测,这里预测输入x对应的值,进行画线
plt.plot(dataSet_x, regr.predict(dataSet_x), color='red', linewidth=1)
plt.show()
输出结果:
0.34761554226
0.34761554226
今天的文章python的线性回归_如何进行线性回归分析分享到此就结束了,感谢您的阅读,如果确实帮到您,您可以动动手指转发给其他人。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/58206.html
