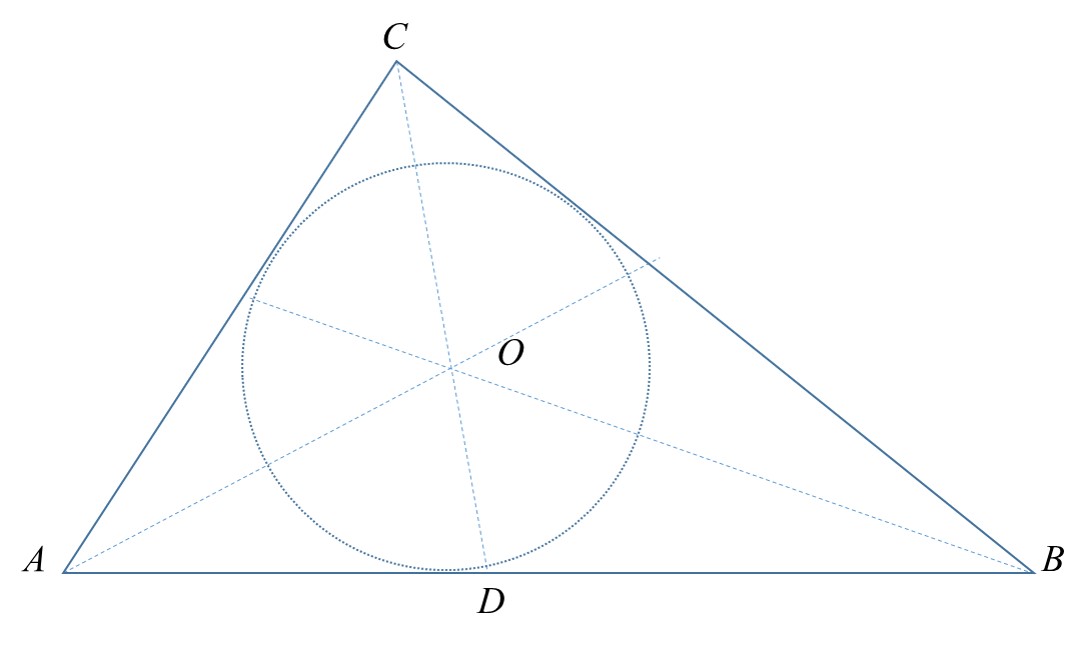
一、对ΔABC重心O来讲有
O A ⇀ + O B ⇀ + O C ⇀ = 0 ⇀ \mathop{OA}\limits ^{\rightharpoonup}+\mathop{OB}\limits ^{\rightharpoonup}+\mathop{OC}\limits ^{\rightharpoonup}=\mathop{0}\limits ^{\rightharpoonup} OA⇀+OB⇀+OC⇀=0⇀
证明:延长CO与线段 A B ‾ \overline{AB} AB交于点D,
根据A、D、B三点共线公式
O D ⇀ = m O A ⇀ + n O B ⇀ \mathop{OD}\limits ^{\rightharpoonup}=m\mathop{OA}\limits ^{\rightharpoonup}+n\mathop{OB}\limits ^{\rightharpoonup} OD⇀=mOA⇀+nOB⇀(其中m+n=1),因为D是线段 A B ‾ \overline{AB} AB的中点,所以有
O A ⇀ + O B ⇀ = 2 O D ⇀ \mathop{OA}\limits ^{\rightharpoonup}+\mathop{OB}\limits ^{\rightharpoonup}=2\mathop{OD}\limits ^{\rightharpoonup} OA⇀+OB⇀=2OD⇀
又因 O C ⇀ = 2 D O ⇀ \mathop{OC}\limits ^{\rightharpoonup}=2\mathop{DO}\limits ^{\rightharpoonup} OC⇀=2DO⇀,
所以 O A ⇀ + O B ⇀ + O C ⇀ = 0 ⇀ \mathop{OA}\limits ^{\rightharpoonup}+\mathop{OB}\limits ^{\rightharpoonup}+\mathop{OC}\limits ^{\rightharpoonup}=\mathop{0}\limits ^{\rightharpoonup} OA⇀+OB⇀+OC⇀=0⇀,得证。
反过来,如果
O A ⇀ + O B ⇀ + O C ⇀ = 0 ⇀ \mathop{OA}\limits ^{\rightharpoonup}+\mathop{OB}\limits ^{\rightharpoonup}+\mathop{OC}\limits ^{\rightharpoonup}=\mathop{0}\limits ^{\rightharpoonup} OA⇀+OB⇀+OC⇀=0⇀
则 O A ⇀ + O B ⇀ + O C ⇀ = ( O D ⇀ + D A ⇀ ) + ( O D ⇀ + D B ⇀ ) + O C ⇀ \mathop{OA}\limits ^{\rightharpoonup}+\mathop{OB}\limits ^{\rightharpoonup}+\mathop{OC}\limits ^{\rightharpoonup}=(\mathop{OD}\limits ^{\rightharpoonup}+\mathop{DA}\limits ^{\rightharpoonup})+(\mathop{OD}\limits ^{\rightharpoonup}+\mathop{DB}\limits ^{\rightharpoonup})+\mathop{OC}\limits ^{\rightharpoonup} OA⇀+OB⇀+OC⇀=(OD⇀+DA⇀)+(OD⇀+DB⇀)+OC⇀
= ( O C ⇀ + 2 O D ⇀ ) + ( D A ⇀ + D B ⇀ ) =(\mathop{OC}\limits ^{\rightharpoonup}+2\mathop{OD}\limits ^{\rightharpoonup})+(\mathop{DA}\limits ^{\rightharpoonup}+\mathop{DB}\limits ^{\rightharpoonup}) =(OC⇀+2OD⇀)+(DA⇀+DB⇀)
= m O D ⇀ + n D A ⇀ = 0 ⇀ =m\mathop{OD}\limits ^{\rightharpoonup}+n\mathop{DA}\limits ^{\rightharpoonup}=\mathop{0}\limits ^{\rightharpoonup} =mOD⇀+nDA⇀=0⇀,
因 O D ⇀ \mathop{OD}\limits ^{\rightharpoonup} OD⇀与 D A ⇀ \mathop{DA}\limits ^{\rightharpoonup} DA⇀线性无关,所以上式要取得 0 ⇀ \mathop{0}\limits ^{\rightharpoonup} 0⇀只有
O C ⇀ + 2 O D ⇀ = 0 ⇀ \mathop{OC}\limits ^{\rightharpoonup}+2\mathop{OD}\limits ^{\rightharpoonup}=\mathop{0}\limits ^{\rightharpoonup} OC⇀+2OD⇀=0⇀并且 D A ⇀ + D B ⇀ = 0 ⇀ \mathop{DA}\limits ^{\rightharpoonup}+\mathop{DB}\limits ^{\rightharpoonup}=\mathop{0}\limits ^{\rightharpoonup} DA⇀+DB⇀=0⇀,
可得 D A ‾ \overline{DA} DA= B D ‾ \overline{BD} BD,以及 C O ‾ \overline{CO} CO=2 O D ‾ \overline{OD} OD,即D是线段 A B ‾ \overline{AB} AB的中点,O为ΔABC的重心。
二、对ΔABC内心O来讲有
a O A ⇀ + b O B ⇀ + c O C ⇀ = 0 ⇀ a\mathop{OA}\limits ^{\rightharpoonup}+b\mathop{OB}\limits ^{\rightharpoonup}+c\mathop{OC}\limits ^{\rightharpoonup}=\mathop{0}\limits ^{\rightharpoonup} aOA⇀+bOB⇀+cOC⇀=0⇀
证明:延长CO与线段 A B ‾ \overline{AB} AB交于点D,
因为 C D ‾ \overline{CD} CD是∠ACB的角平分线,
根据角平分线性质,线段
O A ‾ / O B ‾ = C A ‾ / C B ‾ = D A ‾ / D B ‾ = b / a \overline{OA}/\overline{OB}=\overline{CA}/\overline{CB}=\overline{DA}/\overline{DB}=b/a OA/OB=CA/CB=DA/DB=b/a,
并且
C O ‾ / O D ‾ = C A ‾ / A D ‾ = C B ‾ / B D ‾ = ( C A ‾ + C B ‾ ) / ( A D ‾ + B D ‾ ) = ( a + b ) / c \overline{CO}/\overline{OD}=\overline{CA}/\overline{AD}=\overline{CB}/\overline{BD}=(\overline{CA}+\overline{CB})/(\overline{AD}+\overline{BD})=(a+b)/c CO/OD=CA/AD=CB/BD=(CA+CB)/(AD+BD)=(a+b)/c,
而 C O ‾ \overline{CO} CO与 O D ‾ \overline{OD} OD共线,长度比为 ( a + b ) / c (a+b)/c (a+b)/c,故
( a + b ) O D ⇀ + c O C ⇀ = 0 ⇀ (a+b)\mathop{OD}\limits ^{\rightharpoonup}+c\mathop{OC}\limits ^{\rightharpoonup}=\mathop{0}\limits ^{\rightharpoonup} (a+b)OD⇀+cOC⇀=0⇀,
再根据A、D、B三点共线性质有
a O A ⇀ + b O B ⇀ = ( a + b ) O D ⇀ a\mathop{OA}\limits ^{\rightharpoonup}+b\mathop{OB}\limits ^{\rightharpoonup}=(a+b)\mathop{OD}\limits ^{\rightharpoonup} aOA⇀+bOB⇀=(a+b)OD⇀,所以
a O A ⇀ + b O B ⇀ + c O C ⇀ = ( a + b ) O D ⇀ + c O C ⇀ = 0 ⇀ a\mathop{OA}\limits ^{\rightharpoonup}+b\mathop{OB}\limits ^{\rightharpoonup}+c\mathop{OC}\limits ^{\rightharpoonup}=(a+b)\mathop{OD}\limits ^{\rightharpoonup}+c\mathop{OC}\limits ^{\rightharpoonup}=\mathop{0}\limits ^{\rightharpoonup} aOA⇀+bOB⇀+cOC⇀=(a+b)OD⇀+cOC⇀=0⇀,得证。
反之,若已知 a O A ⇀ + b O B ⇀ + c O C ⇀ = 0 ⇀ a\mathop{OA}\limits ^{\rightharpoonup}+b\mathop{OB}\limits ^{\rightharpoonup}+c\mathop{OC}\limits ^{\rightharpoonup}=\mathop{0}\limits ^{\rightharpoonup} aOA⇀+bOB⇀+cOC⇀=0⇀,则
a O A ⇀ + b O B ⇀ + c O C ⇀ = a\mathop{OA}\limits ^{\rightharpoonup}+b\mathop{OB}\limits ^{\rightharpoonup}+c\mathop{OC}\limits ^{\rightharpoonup}= aOA⇀+bOB⇀+cOC⇀=
a ( O D ⇀ + D A ⇀ ) + b ( O D ⇀ + D B ⇀ ) + c ( O D ⇀ + D C ⇀ ) = a(\mathop{OD}\limits ^{\rightharpoonup}+\mathop{DA}\limits ^{\rightharpoonup})+b(\mathop{OD}\limits ^{\rightharpoonup}+\mathop{DB}\limits ^{\rightharpoonup})+c(\mathop{OD}\limits ^{\rightharpoonup}+\mathop{DC}\limits ^{\rightharpoonup})= a(OD⇀+DA⇀)+b(OD⇀+DB⇀)+c(OD⇀+DC⇀)=
( a + b + c ) O D ⇀ + c D C ⇀ + ( a D A ⇀ + b D B ⇀ ) = (a+b+c)\mathop{OD}\limits ^{\rightharpoonup}+c\mathop{DC}\limits ^{\rightharpoonup}+(a\mathop{DA}\limits ^{\rightharpoonup}+b\mathop{DB}\limits ^{\rightharpoonup})= (a+b+c)OD⇀+cDC⇀+(aDA⇀+bDB⇀)=
( a + b ) O D ⇀ + c O C ⇀ + ( a D A ⇀ + b D B ⇀ ) = 0 ⇀ (a+b)\mathop{OD}\limits ^{\rightharpoonup}+c\mathop{OC}\limits ^{\rightharpoonup}+(a\mathop{DA}\limits ^{\rightharpoonup}+b\mathop{DB}\limits ^{\rightharpoonup})=\mathop{0}\limits ^{\rightharpoonup} (a+b)OD⇀+cOC⇀+(aDA⇀+bDB⇀)=0⇀
因向量 ( ( a + b ) O D ⇀ + c O C ⇀ ) ((a+b)\mathop{OD}\limits ^{\rightharpoonup}+c\mathop{OC}\limits ^{\rightharpoonup}) ((a+b)OD⇀+cOC⇀)与 ( a D A ⇀ + b D B ⇀ ) (a\mathop{DA}\limits ^{\rightharpoonup}+b\mathop{DB}\limits ^{\rightharpoonup}) (aDA⇀+bDB⇀)线性无关,所以上式要取得 0 ⇀ \mathop{0}\limits ^{\rightharpoonup} 0⇀,只有
( a D A ⇀ + b D B ⇀ ) = 0 ⇀ (a\mathop{DA}\limits ^{\rightharpoonup}+b\mathop{DB}\limits ^{\rightharpoonup})=\mathop{0}\limits ^{\rightharpoonup} (aDA⇀+bDB⇀)=0⇀,再由 D A ‾ \overline{DA} DA与 B D ‾ \overline{BD} BD共线,
可得 A D ‾ / D B ‾ = A C ‾ / C B ‾ = b / a \overline{AD}/\overline{DB}=\overline{AC}/\overline{CB}=b/a AD/DB=AC/CB=b/a,即线段 C D ‾ \overline{CD} CD是∠ACB的角平分线,同理可证另两条角平分线 A O ‾ \overline{AO} AO和 B O ‾ \overline{BO} BO,O为ΔABC的内心。另外,
O C ‾ / O D ‾ = ( a + b ) / c \overline{OC}/\overline{OD}=(a+b)/c OC/OD=(a+b)/c。
三、对ΔABC外心O来讲有
O A ⇀ 2 = O B ⇀ 2 = O C ⇀ 2 {\mathop{OA}\limits ^{\rightharpoonup}}^2={\mathop{OB}\limits ^{\rightharpoonup}}^2={\mathop{OC}\limits ^{\rightharpoonup}}^2 OA⇀2=OB⇀2=OC⇀2,
证明:线段 O A ‾ \overline{OA} OA, O B ‾ \overline{OB} OB, O C ‾ \overline{OC} OC为外接圆的半径,所以等长,向量 O A ⇀ 2 {\mathop{OA}\limits ^{\rightharpoonup}}^2 OA⇀2内积为长度的平方。
四、对ΔABC垂心O来讲有
O A ⇀ ⋅ O B ⇀ = O B ⇀ ⋅ O C ⇀ = O C ⇀ ⋅ O A ⇀ \mathop{OA}\limits ^{\rightharpoonup}·\mathop{OB}\limits ^{\rightharpoonup}=\mathop{OB}\limits ^{\rightharpoonup}·\mathop{OC}\limits ^{\rightharpoonup}=\mathop{OC}\limits ^{\rightharpoonup}·\mathop{OA}\limits ^{\rightharpoonup} OA⇀⋅OB⇀=OB⇀⋅OC⇀=OC⇀⋅OA⇀
证明:因为线段 A B ‾ ⊥ C O ‾ \overline{AB}⊥\overline{CO} AB⊥CO,所以
O C ⇀ ⋅ A B ⇀ = 0 \mathop{OC}\limits ^{\rightharpoonup}·\mathop{AB}\limits ^{\rightharpoonup}=0 OC⇀⋅AB⇀=0,因
A B ⇀ = A O ⇀ − B O ⇀ \mathop{AB}\limits ^{\rightharpoonup}=\mathop{AO}\limits ^{\rightharpoonup}-\mathop{BO}\limits ^{\rightharpoonup} AB⇀=AO⇀−BO⇀,所以
O C ⇀ ⋅ ( A O ⇀ − B O ⇀ ) = 0 \mathop{OC}\limits ^{\rightharpoonup}·(\mathop{AO}\limits ^{\rightharpoonup}-\mathop{BO}\limits ^{\rightharpoonup})=0 OC⇀⋅(AO⇀−BO⇀)=0,化简得
O C ⇀ ⋅ A O ⇀ = O C ⇀ ⋅ B O ⇀ \mathop{OC}\limits ^{\rightharpoonup}·\mathop{AO}\limits ^{\rightharpoonup}=\mathop{OC}\limits ^{\rightharpoonup}·\mathop{BO}\limits ^{\rightharpoonup} OC⇀⋅AO⇀=OC⇀⋅BO⇀,即
O C ⇀ ⋅ O A ⇀ = O B ⇀ ⋅ O C ⇀ \mathop{OC}\limits ^{\rightharpoonup}·\mathop{OA}\limits ^{\rightharpoonup}=\mathop{OB}\limits ^{\rightharpoonup}·\mathop{OC}\limits ^{\rightharpoonup} OC⇀⋅OA⇀=OB⇀⋅OC⇀,同理可证
O A ⇀ ⋅ O B ⇀ = O B ⇀ ⋅ O C ⇀ \mathop{OA}\limits ^{\rightharpoonup}·\mathop{OB}\limits ^{\rightharpoonup}=\mathop{OB}\limits ^{\rightharpoonup}·\mathop{OC}\limits ^{\rightharpoonup} OA⇀⋅OB⇀=OB⇀⋅OC⇀,即
O A ⇀ ⋅ O B ⇀ = O B ⇀ ⋅ O C ⇀ = O C ⇀ ⋅ O A ⇀ \mathop{OA}\limits ^{\rightharpoonup}·\mathop{OB}\limits ^{\rightharpoonup}=\mathop{OB}\limits ^{\rightharpoonup}·\mathop{OC}\limits ^{\rightharpoonup}=\mathop{OC}\limits ^{\rightharpoonup}·\mathop{OA}\limits ^{\rightharpoonup} OA⇀⋅OB⇀=OB⇀⋅OC⇀=OC⇀⋅OA⇀。
反之也可证,当
O A ⇀ ⋅ O B ⇀ = O B ⇀ ⋅ O C ⇀ = O C ⇀ ⋅ O A ⇀ \mathop{OA}\limits ^{\rightharpoonup}·\mathop{OB}\limits ^{\rightharpoonup}=\mathop{OB}\limits ^{\rightharpoonup}·\mathop{OC}\limits ^{\rightharpoonup}=\mathop{OC}\limits ^{\rightharpoonup}·\mathop{OA}\limits ^{\rightharpoonup} OA⇀⋅OB⇀=OB⇀⋅OC⇀=OC⇀⋅OA⇀时,O为ΔABC垂心。
今天的文章三角形中重心、内心、外心、垂心向量计算公式分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/5913.html