矩阵扫描原理_Z字形头「建议收藏」

问题描述:
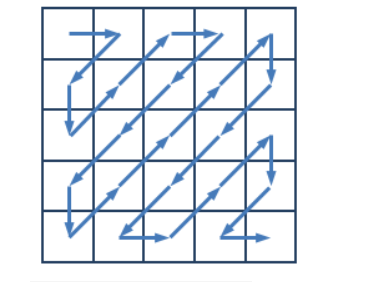
　　在图像编码的算法中，需要将一个给定的方形矩阵进行Z字形扫描(Zigzag Scan)。给定一个n×n的矩阵，Z字形扫描的过程如下图所示：
　　
对于下面的4×4的矩阵，
　　1 5 3 9
　　3 7 5 6
　　9 4 6 4
　　7 3 1 3
　　对其进行Z字形扫描后得到长度为16的序列：
　　1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3
　　请实现一个Z字形扫描的程序，给定一个n×n的矩阵，输出对这个矩阵进行Z字形扫描的结果。

输入格式
　　输入的第一行包含一个整数n，表示矩阵的大小。
　　输入的第二行到第n+1行每行包含n个正整数，由空格分隔，表示给定的矩阵。

输出格式
　　输出一行，包含n×n个整数，由空格分隔，表示输入的矩阵经过Z字形扫描后的结果。

样例输入
4
1 5 3 9
3 7 5 6
9 4 6 4
7 3 1 3

样例输出
1 5 3 9 7 3 9 5 4 7 3 6 6 4 1 3
评测用例规模与约定 1≤n≤500，矩阵元素为不超过1000的正整数。

分析：

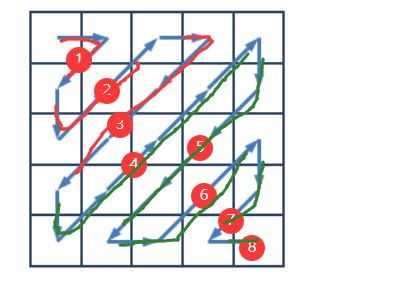
注解：奇数 偶数表示向右向下的次数，以向右开头，如上图所示，1右2下3右4下…

1.通过分析发现，在上三角部分，先向右走一步(遍历完左下)，接着向下走一步(遍历完右上)
2.还发现在上三角部分向右为奇数，向下为偶数。即就是向右，向下，向右，向下以此循环
3.对下三角部分，则相反。向右(遍历右上)为偶数，向下为奇数(遍历左下)。(
具体分析：
若为奇数矩阵：下三角开始为向下(为奇数)，向右(偶数) 。与前半部分相反。
若为偶数矩阵：下三角部分开始为向右(但此时顺序已经更换为偶数，可画图进行演示)，向下(奇数)。
)

可分别用奇数矩阵和偶数矩阵进行演示

代码如下：

可分为上三角，下三角遍历：

#include<stdio.h>
int main(void){ 
   
	int n;
	int i,j,flag;
	scanf("%d",&n);
	int array[n][n];
	int num[n*n],index;
	//输入 
	for(i=0;i<n;i++){ 
   
		for(j=0;j<n;j++){ 
   
			scanf("%d",&array[i][j]);
		}
	}
	//将第一个元素保存 
	index=0;
	num[index++]=array[0][0];
	flag=0;
	i=j=0;
	//进行扫描
	
	while(i<n-1&&j<n-1){ 
   //进行上三角半部分扫描(对角线包括在内) 判定条件为<n-1 是因为在上三角部分遍历完在左下角顶点或者右上角订单点 
		if(flag%2==0){ 
   //向右 
			j++;//向右移动一位 
			flag++;
			while(j>=0){ 
   //遍历左下 
				num[index++]=array[i][j];
				i++;
				j--;
			}
			//将越界下标返回 
			i--;
			j++;
		}else{ 
   //向下 
			i++;//向下移动一位 
			flag++;
			while(i>=0){ 
   //遍历右上 
				num[index++]=array[i][j];
				i--;
				j++; 
			}
			//将越界下标返回 
			i++;
			j--;
		}
	}
	while(i<n&&j<n){ 
   //下三角半部分(与上三角半部分相反)
		if(flag%2==0){ 
   //向右 
			i++;//向右移动一位 
			flag++;
			while(i<n){ 
   //遍历右上 
				num[index++]=array[i][j];
				i++;
				j--;
			}
			//将越界下标返回 
			i--;
			j++;
		}else{ 
   //向下 
			j++;//向下移动一位 
			flag++;
			while(j<n){ 
   //遍历左下 
				num[index++]=array[i][j];
				i--;
				j++;
			}
			//将越界下标返回 
			i++;
			j--;
		}
	}
	for(i=0;i<index;i++){ 
   
		printf("%d ",num[i]);
	}
	return 0;
}

今天的文章矩阵扫描原理_Z字形头「建议收藏」分享到此就结束了，感谢您的阅读，如果确实帮到您，您可以动动手指转发给其他人。