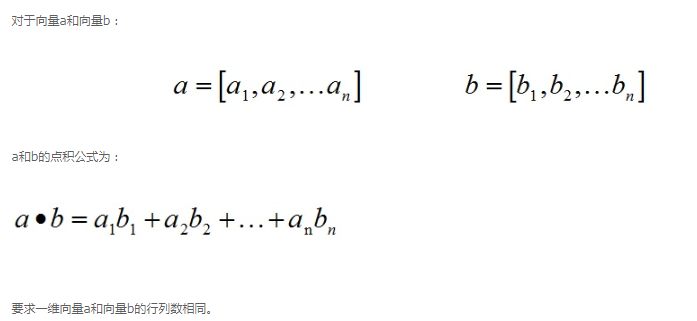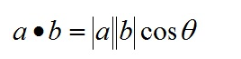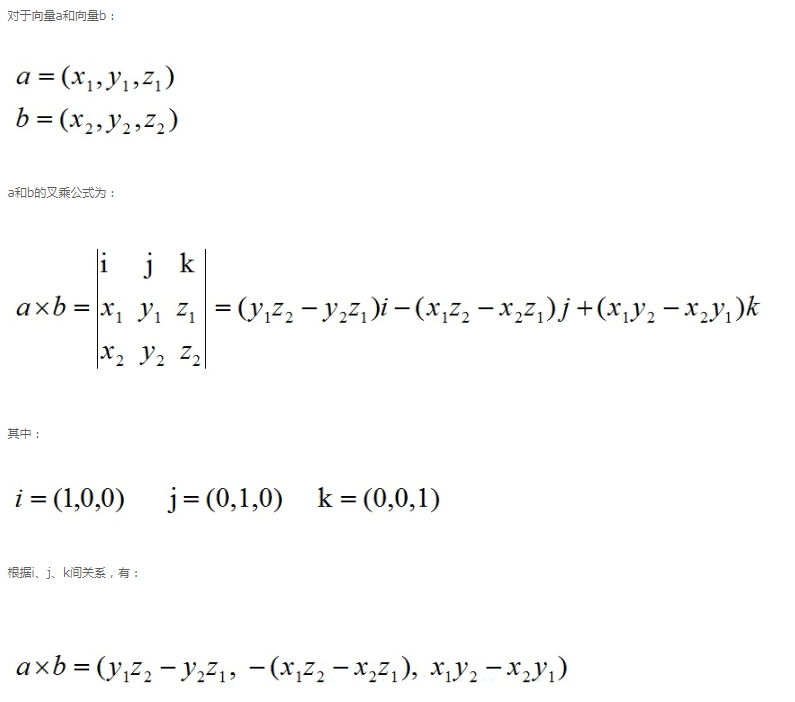向量点乘（内积）和叉乘（外积）

向量是由n个实数组成的一个n行1列（n*1）或一个1行n列（1*n）的有序数组。

1、向量点乘（内积）

向量的点乘，也叫内积，是对两个向量对应位一一相乘之后求和的操作，点乘的结果是一个标量。

1）计算公式：

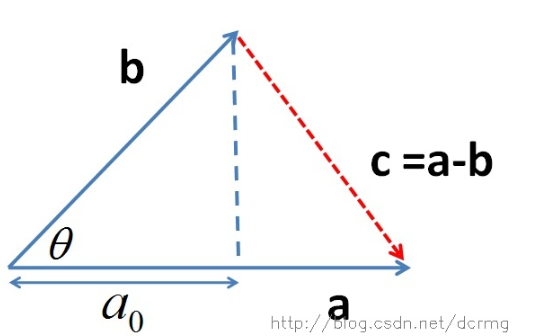
2）几何意义：

1. 表征或计算两个向量之间的夹角
2. b向量在a向量方向上的投影

2、向量差乘

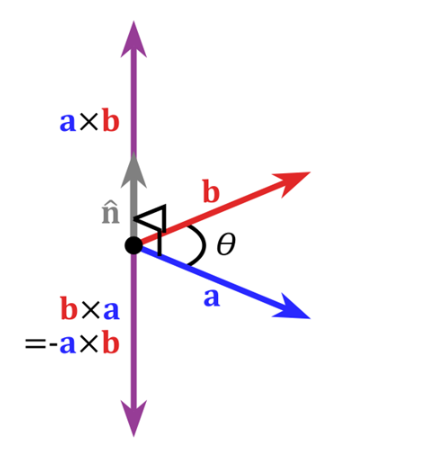
两个向量的叉乘，又叫外积、叉积，叉乘的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量组成的坐标平面垂直。

1）公式：

2）几何意义：

在3D图像学中，叉乘的概念非常有用，可以通过两个向量的叉乘，生成第三个垂直于a，b的法向量，从而构建X、Y、Z坐标系。如下图所示： 

在二维空间中，叉乘还有另外一个几何意义就是：aXb等于由向量a和向量b构成的平行四边形的面积。

今天的文章向量点乘（内积）和叉乘（外积）分享到此就结束了，感谢您的阅读。