树链剖分解析—WYD

首先，树链剖分是个什么东西？
给出一道例题：维护两个操作：
1，修改单点值;2，求x~y路径的权值和；
点数<=100000,操作数量<=100000。
考虑LCA？不行，LCA不能支持修改，极限复杂度(N*N),于是…
接下来，引出数据结构—–树链剖分。

定义与概念：（划重点）

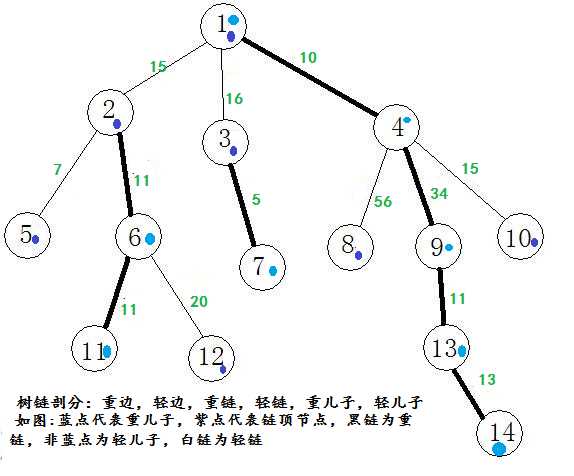
重儿子：父亲节点的所有儿子中子树结点数目最多（size最大）的结点；

轻儿子：父亲节点中除了重儿子以外的儿子；

重边：父亲结点和重儿子连成的边；

轻边：父亲节点和轻儿子连成的边；

重链：由多条重边连接而成的路径；

轻链：由多条轻边连接而成的路径；

请花至少五分钟理解之，上图：

进行变量声明：

size[v]代表以v为根的子树的节点数

dep[v]代表v的深度（根深度为1）

top[v]代表v所在的链顶顶端节点的编号

fa[v]代表v的父亲，son[v]代表v的重儿子。

tree[v]代表节点v在线段树（数据结构）中的编号（dfs序）

pre[v]代表线段树（数据结构）中编号为v的节点所对应的原图中的点编号（tree[v]与pre[v]是互逆的，tree[2]=3,则pre[3]=2.）

开始树链剖分！

Top1：dg1
此递归可以一举求出size,dep,fa与son。
其中dep[f[k][1]]=dep[t]+1,fa[f[k][1]]=t,size[t]+=size[f[k][1]];
son[t]只需通过比较size[f[k][1]]即可得出。(f[k][1]是t的一个儿子）
注意：
如果有多个最大size,任选一个；
叶节点无重儿子，非叶节点有且只有一个重儿子
标程：

void dg1(int t)
{
	size[t]=1;//点本身size=1；
	for (int k=q[t];k;k=ff[k][2]) {
		int h=ff[k][1];//ff[k][1]是前向星中t的一个儿子
		if (h!=fa[t]) {
			fa[h]=t,dep[h]=dep[t]+1;//求fa与dep
			dg1(h);
			size[t]+=size[h];//求size
			if ((!son[t])||(size[son[t]]<size[h])) son[t]=h;
			//求son，选择儿子中最大的size
		}
	}
}
//dg1跑完上图后如此：
size 14 5 2 6 1 3 1 1 3 1 1 1 2 1
son	4 6 7 9	0 11 0 0 13 0 0 0 0 0
 fa	0 1 1 1	2 2 3 4 4 4 6 6 9 13
dep	1 2 2 3 3 3 3 3	3 4 4 4	4 4

Top2：dg2
求出tree，pre与top。
为了用数据结构维护重链，我们要让重链的DFS序连续
标程：

void dg2(int t,int ad)
{
	tot++;
	tree[t]=tot,pre[tot]=t,top[t]=ad;
	//求tree与pre，tree[x]=y则pre[y]=x;
	if (!son[t]) return;
	dg2(son[t],ad);//优先递归重儿子，让重链DFS序连续
	for (int k=q[t];k;k=ff[k][2]) {
		int h=ff[k][1];//dg1中已解释
		if ((h!=fa[t])&&(h!=son[t])) dg2(h,h);
		//如果一个点位于轻链顶端，则它的链顶节点为本身
	}
}
//dg2跑完上图后如此
top	1 2 3 1 5 2 7 8	1 10 2 12 1 1
tree 1 10 8 2 14 11 9 6 3 7 12 13 4 5
pre	1 4 9 13 14 8 10 3 7 2 6 11 12 5

好了，树链剖分结束了。

WTF？这就结束了？说好150+行的代码呢？

是的，树链剖分的主要操作已经结束，我们将树转换成了一条条的链加以维护。
不过，还有一个遗留难题：为什么树链剖分的时间复杂度是O(nlog^2n)?
有两条性质：
1.若(u,v)为轻边（u是v父亲），则size[u]>size[v]*2。
这个显然，如果不满足size[u]>size[v]*2，size[v]必然不小于其它儿子的size，那么(u,v)不该是轻边。
2.从根结点到任意结点的路所经过的轻重链的个数必定都小与O(logn)；
这个不显然，但易证。
先证轻链：因为1性质，如果(u,v)为轻边，从u到v的size至少减一半；
那么最多只能经过log(n)层。
重链与轻链是并行的，所以重链最多有log(n)+1条
证毕。
对于这些链，用线段树维护即可。
模板题：JZOJ2256 ZJOI2008 树的统计

#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <cstring>
using namespace std;
int i,j,k,m,n,o,p,l,s,t,x,y,tot;
struct node{int sum,max,l,r;}f[1200001];
int ff[600001][3],q[600001],fa[300001],son[300001],dep[300001],size[300001];
int top[300001],tree[300001],pre[300001],a[300001];
char ch[7];
void insert(int x,int y)
{ t++,ff[t][1]=y,ff[t][2]=q[x],q[x]=t; }
void downdata(int x)
{
    int xx=x*2,yy=x*2+1;
    f[x].sum=f[xx].sum+f[yy].sum;
    f[x].max=max(f[xx].max,f[yy].max);
}
void change(int x,int v,int ad)
{
    if (f[x].l==f[x].r) f[x].max=ad,f[x].sum=ad;
    else {
        int mid=(f[x].l+f[x].r)/2;
        if (v<=mid) change(x*2,v,ad); else change(x*2+1,v,ad);
        downdata(x);
    }
}
void make(int x,int l,int r)
{
    f[x].l=l,f[x].r=r;
    if (l==r) f[x].sum=f[x].max=a[pre[l]];
    else {
        int mid=(l+r)/2;
        make(x*2,l,mid);make(x*2+1,mid+1,r);
        downdata(x);
    }
}
void dg1(int t)
{
    size[t]=1;
    for (int k=q[t];k;k=ff[k][2]) {
        int h=ff[k][1];
        if (h!=fa[t]) {
            fa[h]=t,dep[h]=dep[t]+1;
            dg1(h);
            size[t]+=size[h];
            if ((!son[t])||(size[son[t]]<size[h])) son[t]=h;
        }
    }
}
void dg2(int t,int ad)
{
    tot++;
    tree[t]=tot,pre[tot]=t,top[t]=ad;
    if (!son[t]) return;
    dg2(son[t],ad);
    for (int k=q[t];k;k=ff[k][2]) {
        int h=ff[k][1];
        if ((h!=fa[t])&&(h!=son[t])) dg2(h,h);
    }
}
int getsum(int t,int x,int y)
{
    if ((f[t].l>=x)&&(f[t].r<=y)) return f[t].sum;
    int mid=(f[t].l+f[t].r)/2,sum=0;
    if (x<=mid) sum+=getsum(t*2,x,y);
    if (y>mid) sum+=getsum(t*2+1,x,y);
    return sum;
}
int getmax(int t,int x,int y)
{
    if ((f[t].l>=x)&&(f[t].r<=y)) return f[t].max;
    int mid=(f[t].l+f[t].r)/2,Max=-2147483648;
    if (x<=mid) Max=max(Max,getmax(t*2,x,y));
    if (y>mid) Max=max(Max,getmax(t*2+1,x,y));
    return Max;
}
int findmax(int x,int y) 
{
    int xx=top[x],yy=top[y],maxans=-2147483648;
    while (xx!=yy) {
        if (dep[xx]<dep[yy]) swap(xx,yy),swap(x,y);
        maxans=max(maxans,getmax(1,tree[xx],tree[x]));
        x=fa[xx],xx=top[x];
    }   
    if (dep[x]>dep[y]) swap(x,y);
    maxans=max(maxans,getmax(1,tree[x],tree[y]));
    return maxans;
}
int findsum(int x,int y) 
{
    int xx=top[x],yy=top[y],sumans=0;
    while (xx!=yy) {
        if (dep[xx]<dep[yy]) swap(xx,yy),swap(x,y);
        sumans+=getsum(1,tree[xx],tree[x]);
        x=fa[xx],xx=top[x];
    }   
    if (dep[x]>dep[y]) swap(x,y);
    sumans+=getsum(1,tree[x],tree[y]);
    return sumans;
}
int main()
{
    scanf("%d",&n);
    for (i=1;i<=n-1;i++) {
        scanf("%d%d",&x,&y);
        insert(x,y);insert(y,x);
    }
    for (i=1;i<=n;i++) scanf("%d",&a[i]);
    t=0;dep[1]=1;
    dg1(1);
    dg2(1,1);
    make(1,1,n);
    scanf("%d",&m);
    for (i=1;i<=m;i++) {
        scanf("%s",&ch);
        scanf("%d%d",&x,&y);
        if (ch[1]=='H') {
            change(1,tree[x],y);
        } else {
            printf("%d\n",ch[1]=='M'?findmax(x,y):findsum(x,y));
        }
    }
}

今天的文章树链剖分解析—WYD分享到此就结束了，感谢您的阅读。