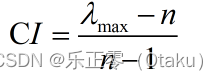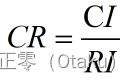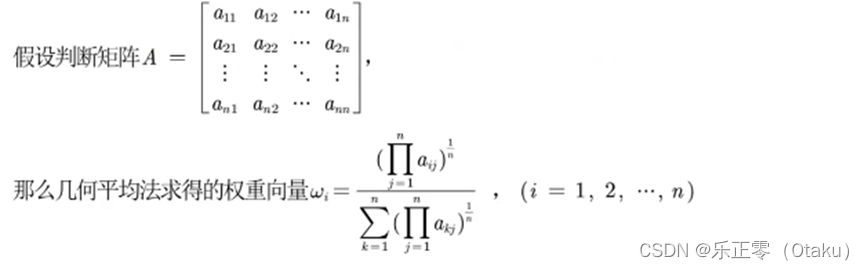目录
前言
本文大部分是对于数学建模清风老师的课程学习总结归纳而来,我的理解可能有错误,大家发现错误可以在评论区批评指正,课程地址:《数学建模清风》
一、模型定义与思想
层次分析法(TheAnalytic Hierarchy Process即AHP)是由美国运筹学家、匹兹堡大学教授T.L.Saaty于20世纪70年代创立的一种系统分析与决策的综合评价方法,是在充分研究了人类思维过程的基础上提出来的,它较合理地解决了定性问题定量化的处理过程。
AHP的主要特点是通过建立递阶层次结构,把人类的判断转化到若干因素两两之间重要度的比较上,从而把难于量化的定性判断转化为可操作的重要度的比较上面。在许多情况下,决策者可以直接使用AHP进行决策,极大地提高了决策的有效性、可靠性和可行性,但其本质是一种思维方式,它把复杂问题分解成多个组成因素,又将这些因素按支配关系分别形成递阶层次结构,通过两两比较的方法确定决策方案相对重要度的总排序。整个过程体现了人类决策思维的基本特征,即分解、判断、综合,克服了其他方法回避决策者主观判断的缺点。
二、模型步骤与实现
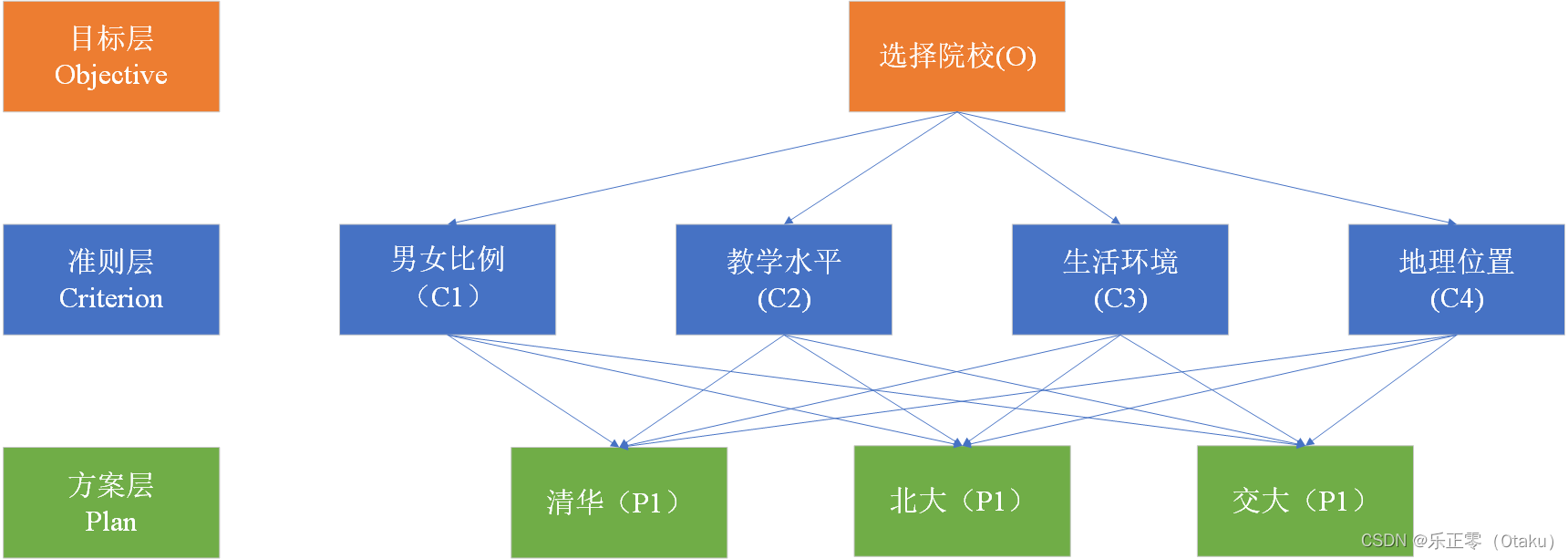
1.分析系统中各因素之间的关系,建立系统的递阶层次结构
以院校的选择为例:
2.通过两两进行比较构造判断矩阵
我们的目标是通过我们构建的判断矩阵,去计算每个因素所占的权重/满意程度,最终我们会制造出一个权重——打分表,如下:
指标权重 |
清华(P1) |
北大(P2) |
交大(P3) |
|
|
男女比例(C1) |
||||
教学水平(C2) |
||||
生活环境(C3) |
||||
地理位置 (C4) |
实际上的建模结果就是要填满权重矩阵,即这个表格:
- 其中,蓝色一列代表男女比例、教学水平、生活环境以及地理位置的权重之和为1。(实际上就是准则层关于上一层目标层的重要性)
- 然后同一颜色每一横行,就是三种方案相对于准则层的重要性。如:橙色一行 代表的就是清华、北大、交大关于男女比例的权重,以此类推。
如何填满这个表格,就需要用判断矩阵得出,这也是构造判断矩阵的意义!
2.1构造评价矩阵的个数
由上文可知得到这个判断矩阵实际上要分别得出准则层关于目标层的一组权重向量,方案层关于准则层的五组权重向量,实际上我们就需要构造出一个准则层关于目标层的判断矩阵以及五个方案层关于准则层的矩阵,一共5个判断矩阵。(这里采用分治的思想)最终在经过权重计算每组得出一组权重向量,填到相应的表格中。构造的5个判断矩阵如下:
PS:在打分的时候应当采取专家团打分的方式,或通过网上资料、现有的指标文献来进行合理科学地取舍。
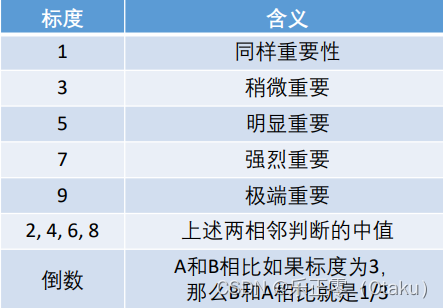
PPS:重要性(满意度)的打分可以参考这个表:
|
O |
C1 |
C2 |
C3 |
C4 |
|
C1 |
1 |
1/5 |
1/3 |
1/4 |
|
C2 |
5 |
1 |
4 |
2 |
|
C3 |
3 |
1/4 |
1 |
1/3 |
|
C4 |
4 |
1/2 |
3 |
1 |
比较矩阵1
|
C1 |
P1 |
P2 |
P3 |
|
P1 |
1 |
1/2 |
1/3 |
|
P2 |
2 |
1 |
2 |
|
P3 |
3 |
1/2 |
1 |
比较矩阵2
|
C2 |
P1 |
P2 |
P3 |
|
P1 |
1 |
1 |
2 |
|
P2 |
1 |
1 |
2 |
|
P3 |
1/2 |
1/2 |
1 |
比较矩阵3
|
C3 |
P1 |
P2 |
P3 |
|
P1 |
1 |
1 |
1/2 |
|
P2 |
1 |
1 |
1/2 |
|
P3 |
2 |
2 |
1 |
比较矩阵4
|
C4 |
P1 |
P2 |
P3 |
|
P1 |
1 |
1 |
2 |
|
P2 |
1 |
1 |
2 |
|
P3 |
1/2 |
1/2 |
1 |
比较矩阵5
PS:由于这些都是根据小明(虚构)所要选择的人生方向和各大学所有的特性进行打分,并无其他恶意比较的意思,只是各有优势,请勿当真。
由此可见,在建立层次关系之后,我们需要构建5(n+1)个比较矩阵,一个是决策层自身的重要程度,另外四个是决策层对于目标层的重要程度。
3.进行一致性检验
只有通过了一致性检验的矩阵才能够使用!
为什么要进行一致性检验?
假设:清华 = P1、北大 = P2、交大 = P3,
| C | P1 | P2 | P3 |
| P1 | 1 | 2 | 1 |
| P2 | 1/2 | 1 | 2 |
| P3 | 1 | 1/2 | 1 |
那么由矩阵可以看出,清华比北大指标C好一点 P1 > P2,清华和交大指标C一样好 P1 = P3,北大比交大指标C好一点 P2 > P3,出现了 矛盾!
这里就不得不提出一个概念叫做 一致矩阵,它在正互反矩阵性质的基础上没有以上的矛盾,可以说:一致矩阵是正互反矩阵的特例。
将上面的矩阵进行改良,得到一致矩阵:
| C | P1 | P2 | P3 |
| P1 | 1 | 2 | 4 |
| P2 | 1/2 | 1 | 2 |
| P3 | 1/4 | 1/2 | 1 |
它比正互反矩阵多出两个性质:
- aij = i的重要程度 / j的重要程度,ajk = j的重要程度 / k的重要程度,aik = i的重要程度 / k的重要程度 = aij × ajk。
- 矩阵各行(各列)之间成倍数关系。
我们进行构造矩阵大多是正互反矩阵,难免会出现矛盾,即不容易构造出一致性矩阵,但是我们可以向一致性矩阵靠拢,只要这个差距(CR)不超过一个范围(0.1)那么这个判断矩阵也是可以使用的。这个判断差距的过程叫做 一致性检验。
一致性检验的步骤如下:
第一步:计算一致性指标 CI
第二步:查找对应的平均随机一致性指标 RI
PS:在实际运用中,n很少超过10,如果指标的个数大于10,则可以考虑建立二级指标体系(或者使用之后的进阶模型),RI直接查表使用即可。
第三步:计算一致性比例CR
如果 CR < 0.1, 则可认为判断矩阵的一致性可以接受;否则需要对判断矩阵进行修正。
在上面的例子中的评价矩阵都已通过了一致性检验。
4.计算各元素权重
一共有三种方法可以计算权重:
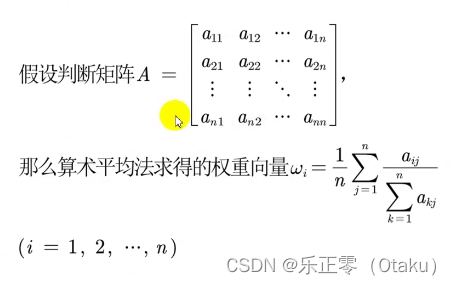
(1)算数平均法
- 第一步:将判断矩阵按照列归一化(每一个元素除以其所在列的和)
- 第二步:将归一化的各列相加(按行求和)
- 第三步:将相加后得到的向量中每个元素除以n可得到权重向量
表达式如下:
(2)几何平均法求权重
- 第一步:将A的元素按照行相乘得到一个新的列向量
- 第二步:将新的向量的每个分量开n次方
- 第三步:对该列向量进行归一化即可得到权重向量
(3)特征值法求权重
因为我们的判断矩阵一致性可以接受,那么我们可以仿照一致矩阵权重的求法:
- 第一步:求出矩阵A的最大特征值以及其对应的特征向量
- 第二步:对求出的特征向量进行归一化即可得到我们的权重
PS:在比赛中我们可以使用三种方法计算权重,然后加上这样一段话:不同的计算方法可能会导致结果有所偏差,为了保证结果的稳健性,本文采用了三种方法分别求出了权重,再根据得到的权重矩阵计算各方案的得分,并进行排序和综合分析,这样避免了采用单一方法所产生的偏差,得出的结论将更全面、更有效。
5.计算各层元素对系统目标的合成权重,并进行排序
通过上面的计算,我们可以得到各个元素的权重,将前面的卷重矩阵进行填充(四舍五入后)如下:
指标权重 |
清华(P1) |
北大(P2) |
交大(P3) |
|
|
男女比例(C1) |
0.07 |
0.17 |
0.48 |
0.35 |
|
教学水平(C2) |
0.49 |
0.40 |
0.40 |
0.20 |
|
生活环境(C3) |
0.14 |
0.25 |
0.25 |
0.50 |
|
地理位置 (C4) |
0.30 |
0.4 |
0.4 |
0.2 |
我们对每个目标的元素得分与权重对应相乘再相加,用excel进行计算,最终得分为:
P1=0.36 P2=0.38 P3=0.25因此选择北大
三、模型局限性和使用技巧
1.局限性
- 评价的决策层不能太多,太多的话n会很大,判断矩阵和一致矩阵差异可能会很大。因为平均随机一致性指标 RI 的表格中 n 最多是15,因此应该根据实际情况选择是否应用此方法。
- 如果决策层中指标的数据是已知的,那么层次分析法不容易将这些已知数据应用在其中。如拿上面的例题举例:如果已知男女比例、教学水平、生活环境、地理位置在三所高校的一些数据,那么如何将这些数据转化为构造判断矩阵的依据,只能为其提供一定的文字说明,而不容易将数据应用到其中。
2.使用技巧
- 在实际建模中,判断矩阵的数值都是人为填的,具有一定的主观性存在,这时应该搜寻相应的数据让人信服(最好能是文献中已经论证过的指标),不能空口无凭。
- 如果说只想拿到的决策因素的权重向量,那大可不必这么麻烦,在第一步递阶层次结构的时候,只需要目标层和准则层即可,构造判断矩阵也只需要构造出一个,并进行检验,检验通过了,差不多就拿到了权重向量。
四、模型总结
这个模型对于新手来说比较好上手,但主观性太强,需要用一些技巧让其客观性体现出来,之后会有更多的评价类模型来弥补这个漏洞。
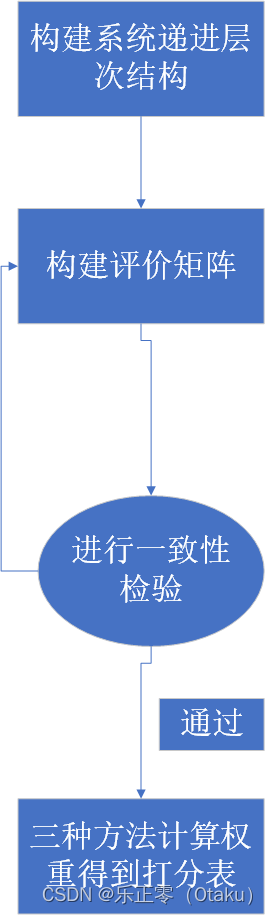
模型步骤回顾:
代码实现:
%输入判断矩阵
clear
clc
A = input('请输入判断矩阵A=');
[r,c] = size(A);
ERROR = 0;
if r ~= c || r <= 1
ERROR = 1;
end
if ERROR == 0
n = size(A,1);
if sum(sum(A <= 0)) > 0
ERROR = 2;
end
end
if ERROR == 0
if n > 15
ERROR = 3;
end
end
if ERROR == 0
if sum(sum(A' .* A ~= ones(n))) > 0
ERROR = 4;
end
end
if ERROR == 1
disp('请检查矩阵A的维数是否不大于1或不是方阵');
return
elseif ERROR == 2
disp('请检查矩阵A中是否元素小于等于0');
return
elseif ERROR == 3
disp('矩阵A的维数超过了15,请减少准则层的数量');
return
elseif ERROR == 4
disp('请检查矩阵A中是否存在i,j不满足A_ij * A_ji = 1');
return
end
%% 方法1:算术平均法求权重
%第一步:将判断矩阵按照列归一化处理(每一个元素除以其所在列的和)
Sum_A = sum(A,1);
n = size(A,1);
SUM_A = repmat(Sum_A,n,1);
Stand_A = A ./ SUM_A;
%第二步:将归一化的各列相加(按行求和)
ans1 = sum(Stand_A,2);
%第三步:将相加后得到的向量中每个元素除以n,即可得到权重
disp('算术平均法求权重的结果为:');
disp(ans1./n);
%% 方法2:几何平均法求权重
%第一步:将A的元素按照行相乘得到一个新的列向量
Product_A = prod(A,2);
%第二步:将新的向量的每个分量开n次方
Product_n_A = Product_A .^(1/n);
%对该向量进行归一化处理即可得到权重向量
%将这个列向量中的每一个元素除以这一个向量的和即可
disp('几何平均法求权重的结果为:');
disp(Product_n_A ./ sum(Product_n_A,1));
%% 方法3:特征值法求权重
%第一步:求出矩阵A的最大特征值以及其对应的特征向量
[V,D] = eig(A);%V是特征向量,D是由特征值构成的对角矩阵
Max_eig = max(max(D));
[r,c] = find(D == Max_eig,1);
%找到最大特征值,记录他的行与列
%第二步:对求出的特征向量进行归一化处理即可得到权重向量
disp('特征值法求权重的结果为');
disp(V(:,c) ./ sum(V(:,c)));
%我们先根据上面找到的最大特征值的列数c找到对应的特征向量,然后再进行标准化
%% 计算一致性比例CR
CI = (Max_eig - n)/(n-1);
RI = [0,0.001,0.52,0.89,1.12,1.26,1.41,1.46,1.49,1.52,1.54,1.56,1.58,1.59];
%这里的RI最多支持n = 15
CR = CI/RI(n);
disp(['一致性指标CI=',num2str(CI)]);
disp(['一致性比例CR=',num2str(CR)]);
if CR < 0.10
disp('因为CR < 0.10,所以该判断矩阵A的一致性可以接受!');
else
disp('注意:CR >= 0.10,因此该判断矩阵A需要进行修改!');
end今天的文章《零基础数学建模》——层次分析法分享到此就结束了,感谢您的阅读。
版权声明:本文内容由互联网用户自发贡献,该文观点仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 举报,一经查实,本站将立刻删除。
如需转载请保留出处:https://bianchenghao.cn/60919.html